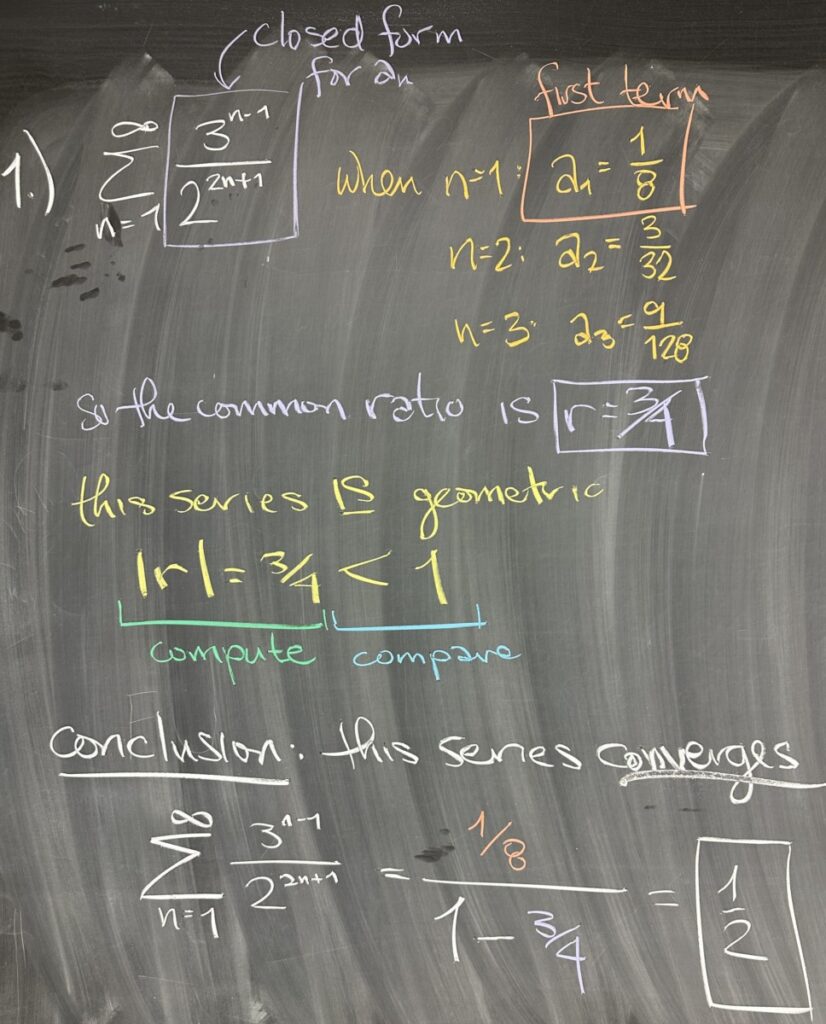
Today’s first quiz question asked about the convergence of the infinite sum: \(\displaystyle\sum^\infty_{n=1}\frac{3^{n-1}}{2^{2n+1}}\). Looking at the closed form for \(a_n=\dfrac{3^{n-1}}{2^{2n+1}}\), we see that \(n\) only appears in the exponents of the expression — giving the impression that this should be a geometric sequence (\(a_n\)) and series (\(\sum a_n\)). When working with a suspected geometric sequence or series, it is important to carefully compute the initial term and the common ratio.
After computing \(a_1=\frac18\), \(a_2=\frac{3}{32}\), and \(a_3=\frac{9}{128}\), we conclude that \(a_n\) is indeed a geometric sequence, and the common ratio is \(r=\frac34\). Since that makes the series geometric as well, we check that the absolute value of the common ratio is less than one (it is) — and conclude that this series converges.
For convergent geometric series, we can determine the infinite sum as the result of the initial term divided by \((1-r)\) — in this case \[\sum^\infty_{n=1}\frac{3^{n-1}}{2^{2n+1}}=\frac{\frac18}{1-\frac34}=\frac{1}{2}\]

The second quiz question asked about the meaning of a sequence “having a limit”, and the meaning of a sequence “converging.” These are actually two ways of saying the exact same thing — a sequence that “has a limit” is “convergent” — and any “convergent” sequence “has a limit.”
If a sequence has an explicit closed form, \(a_n=f(n)\), then “having a limit” is as straightforward as computing \(\displaystyle\lim_{n\to\infty} f(n)\). If this limit exists, the sequence “converges” (identically, “has a limit”).
Another way to describe this is to say that \(f(n)\) has asymptotic behavior as \(n\to\infty\), or that the values of \(a_n\) grow ever closer (or remain equal to) some real number \(L\) as \(n\to\infty\).

The final question asks for a comparison between sequences, \(a_n\), their sequence of partial sums \(\displaystyle s_n=\sum^n a_n\), and the infinite sum \(\displaystyle \sum^\infty a_n\).
Sequences are typically described by their closed form \(a_n=f(n)\), while their sequence of partial sums typically do not have a closed form. Instead, \(s_n=f(1)+f(2)+f(3)+\ldots+f(n)\). These are two different (but related) sequences.
The infinite sum is the limit of the sequence of partial sums — and this limit may or may not exist. Typically, computing this limit is impossible, as we will not have a closed form for \(s_n\) (except in the case of geometric series).
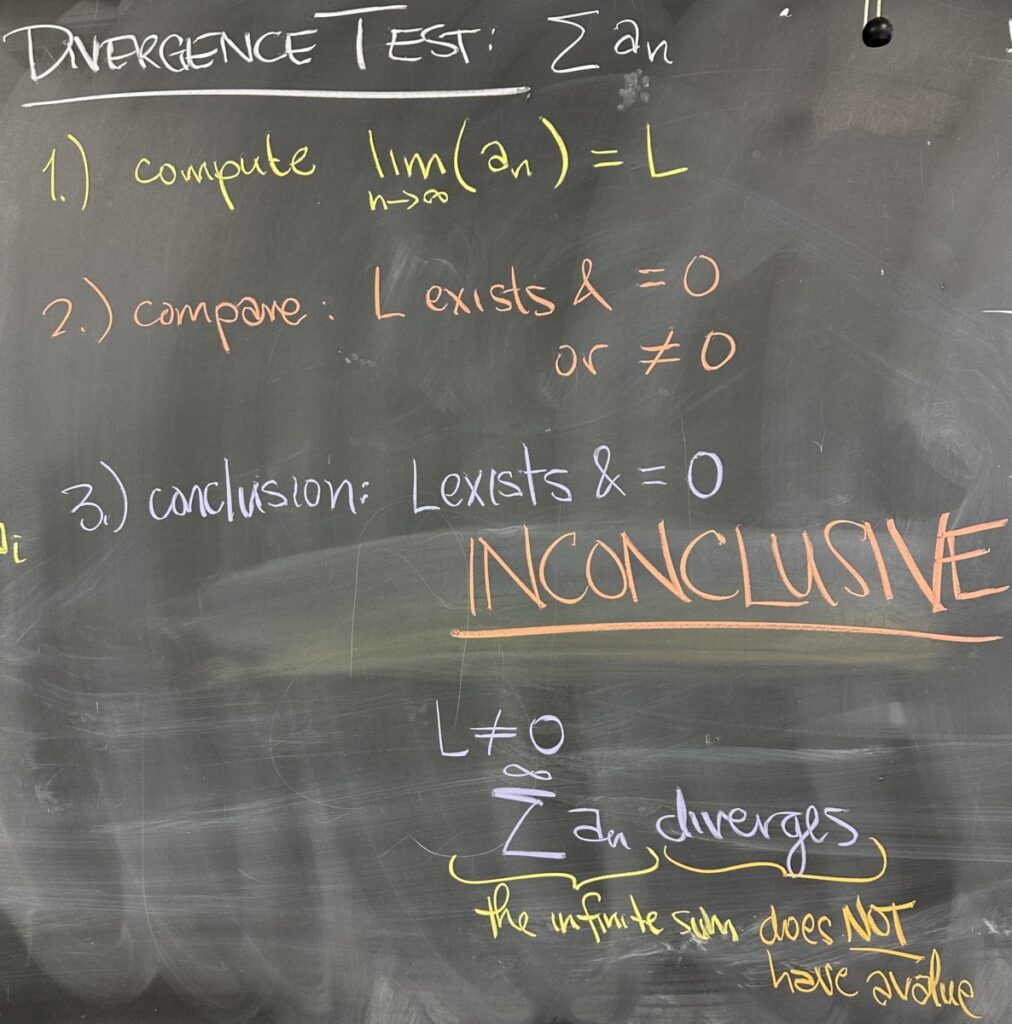
The Divergence Test, we discussed last lecture, allows us to draw conclusions about the divergence of the series, \(s_n\), from the limit of the sequence, \(\displaystyle\lim_{n\to\infty}a_n\).
If the limit of the sequence is anything other than zero, then the series must diverge. In other words, the sequence of partial sums does not have a limit — or the infinite sum does NOT have a value.
It is VERY IMPORTANT to note that if the limit of the sequence is zero, then the series might converge or it might diverge — this test is inconclusive if the limit of the sequence is zero.

For now, we are only going to consider series for sequences that are positive. That is to say, \(a_n > 0\) for all \(n\). This causes the sequence of partial sums to be monotone increasing.
Furthermore, for the question of convergence or divergence of any series, it is irrelevant what \(n\)-value is used to start the partial sums. If the “tail” of the series is finite (convergent), then adding more terms at the “front” of the series will not change the finite-ness (convergence) of the series. Adding more terms would change the total — but it doesn’t matter, because we generally won’t be able to ascertain the total in the first place.
Similarly, if the “tail” of the series is divergent, then adding more terms at the “front” of the series will not change the divergent-ness.
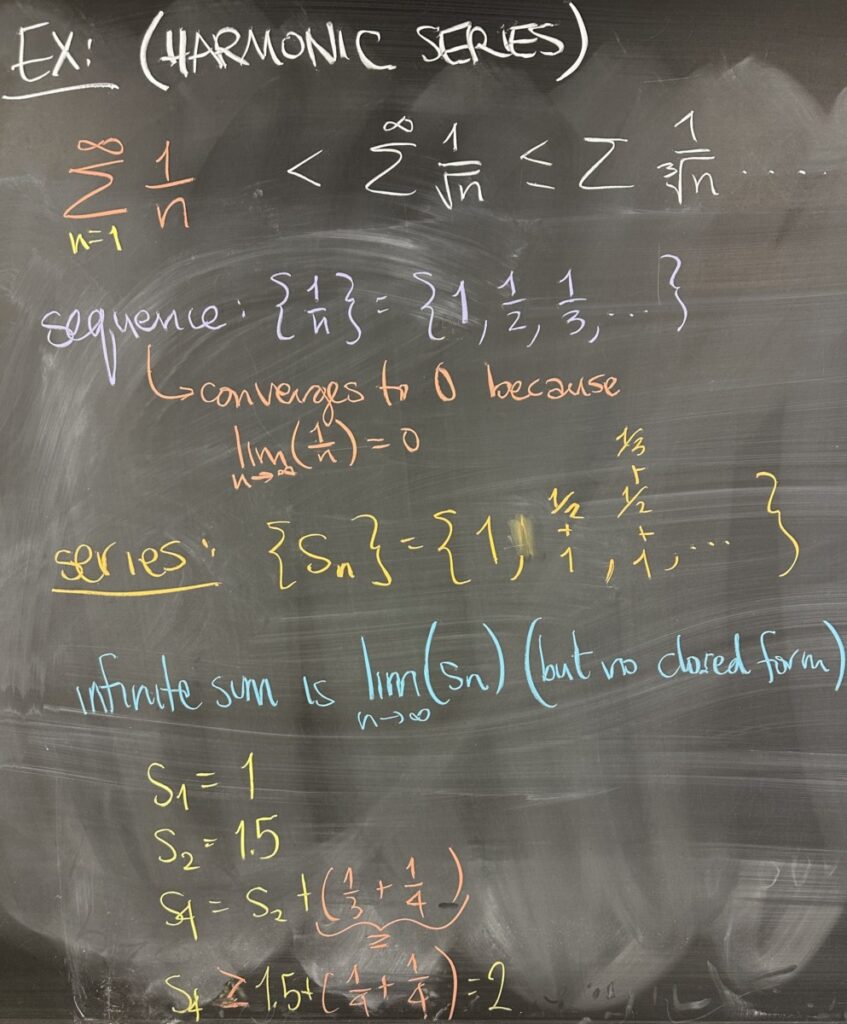
Then we take a look at an important example — the “harmonic series”. This series is specifically \(\displaystyle\sum^\infty \frac1n\).
The sequence, \(a_n=\frac1n\), converges to zero — so the divergence test is inconclusive. Without another test to use, we’ll have to try to look at \(s_n\) — but without a closed form, we have nothing to take the limit of.
We won’t look at all of the terms of the \(s_n\) sequence for \(a_n=\frac1n\), but to start we note that \(s_1=1\) and \(s_2=1.5\). Then \(s_4=s_2+(\frac13+\frac14)\), and we notice that \(\frac13>\frac14\), so \(s_4>1.5+(\frac14+\frac14)=2\).
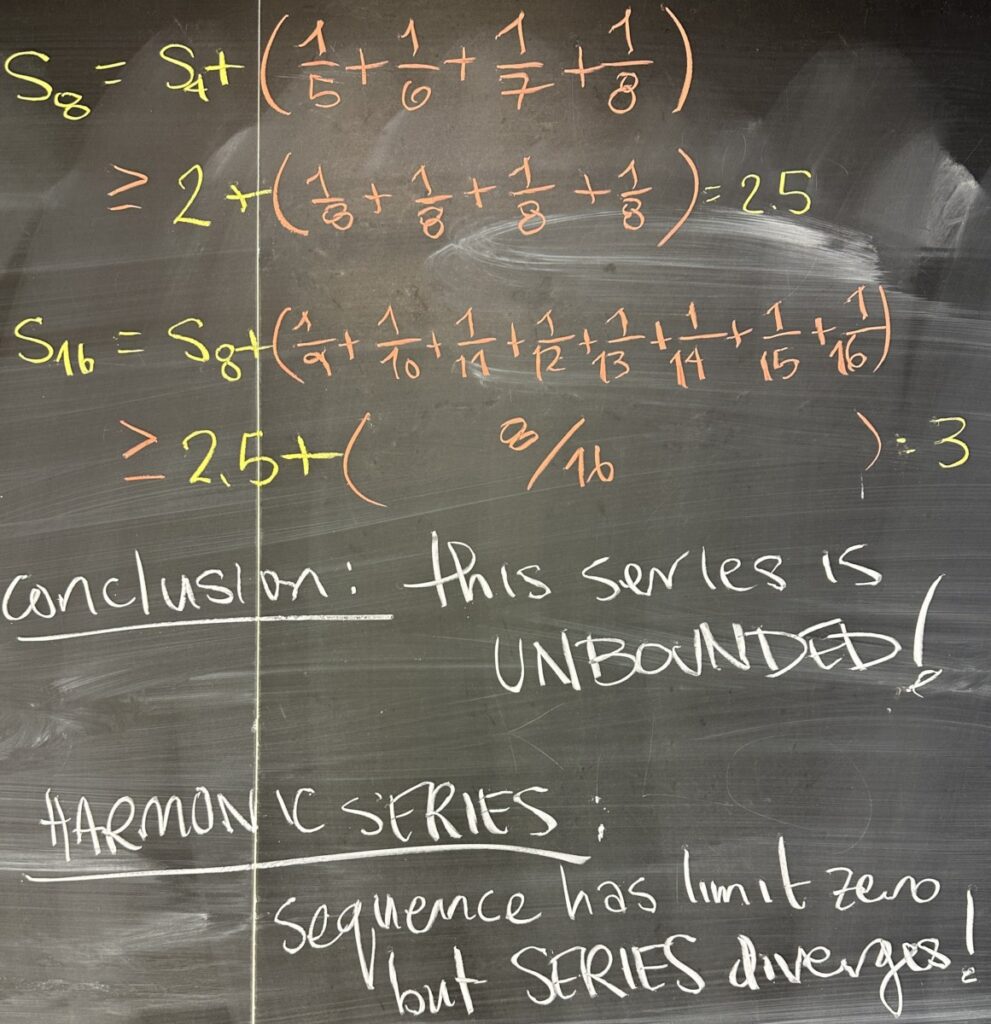
Then we skip ahead to \(s_8=s_4+(\frac15+\frac16+\frac17+\frac18)\) and apply the same logic that \(\frac15>\frac18\), \(\frac16>\frac18\), and \(\frac17>\frac18\), so \(s_8>2+(\frac18+\frac18+\frac18+\frac18)=2.5\).
Jumping to \(s_{16}\), we again use the same logic to conclude that \(s_{16}>3\).
By repeatedly applying this pattern we see that the series, \(s_n\), is unbounded. So, this example is important because it is a sequence \(a_n=\frac1n\) that converges to zero, yet its series \(\sum\frac1n\) is divergent.
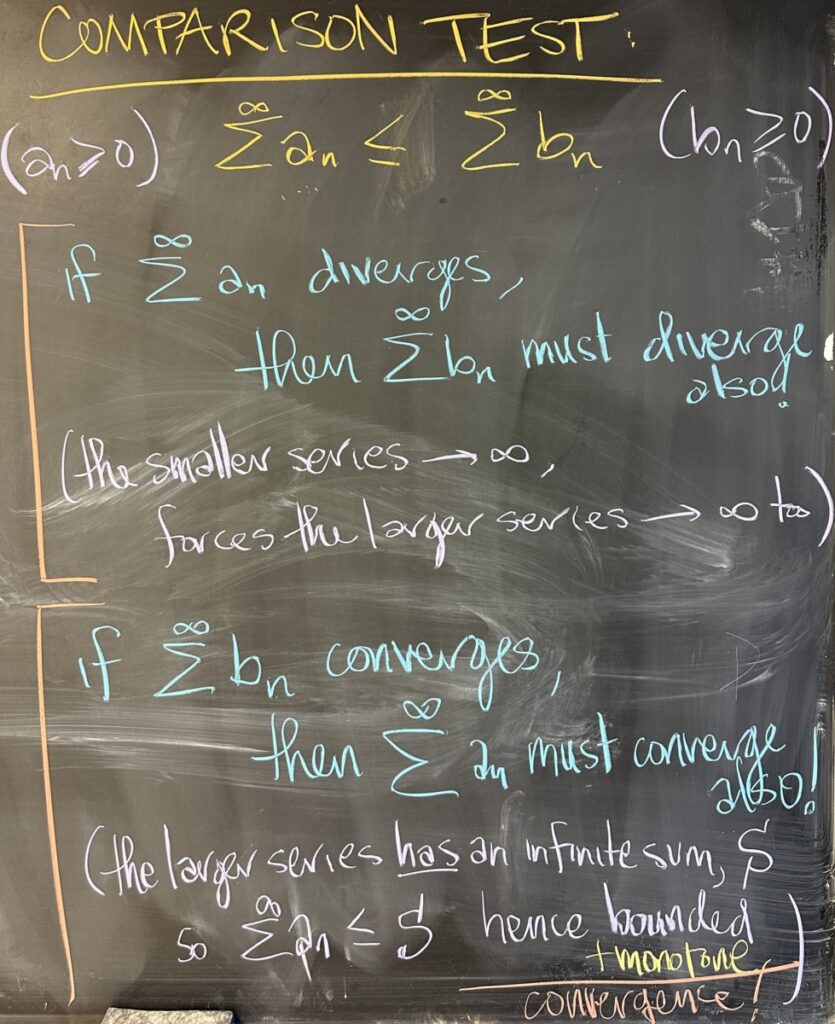
Wrapping up today’s lesson, we consider what happens when comparing two series (specifically series that are built from positive sequences).
If the smaller of the two series is divergent (the infinite sum has no limit — unbounded), then the larger series must also diverge. This must happen, as the larger series is greater than something which is unbounded and must therefore be unbounded itself.
On the other hand, if the larger of the two series is convergent, then the smaller series must also converge. This must happen because when the larger series converges to a finite value, it serves as an upper bound for the smaller series. As a result, the smaller series is both monotone increasing and has an upper bound, which forces it to converge.




Recent Comments