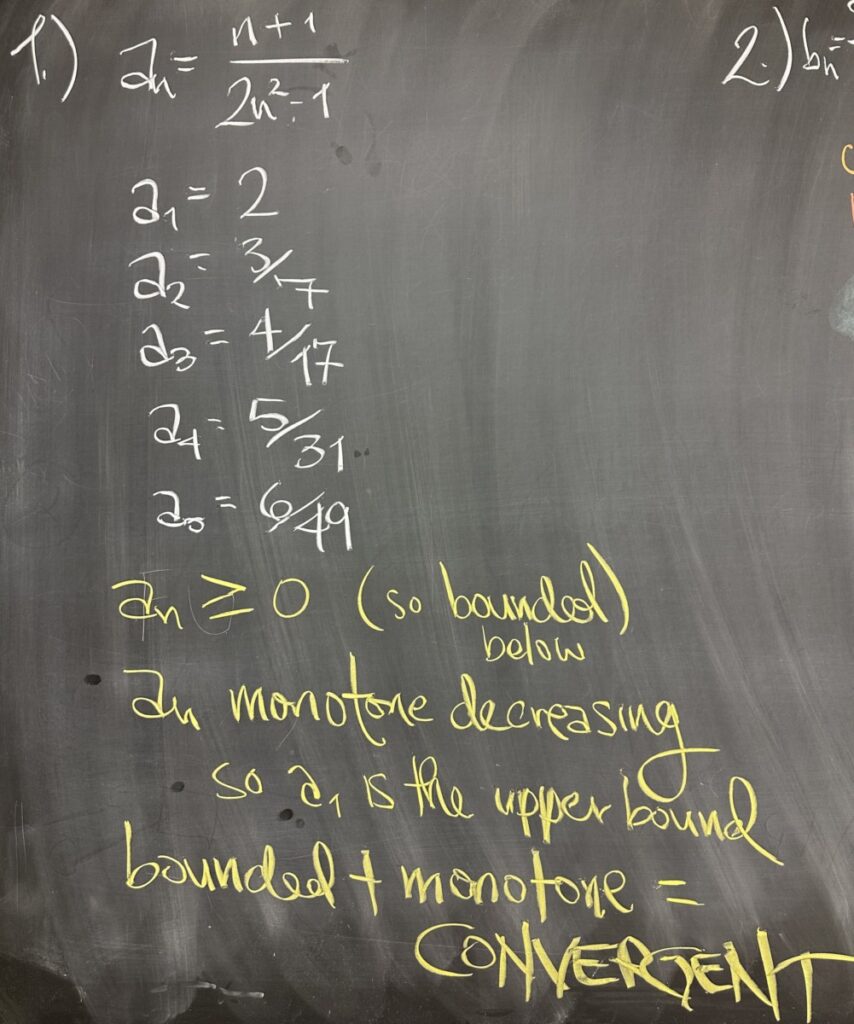
The first problem on today’s quiz asked for the first five terms of the sequence (given in closed form: \(a_n = f(n) = \frac{n+1}{2n^2-1}\)). Finding the first five terms is as straightforward as finding the value of the function when \(n=1\), \(n=2\), \(n=3\), \(n=4\), and \(n=5\). The five values are \(\{2,\frac{3}{7},\frac{4}{17},\frac{5}{31},\frac{6}{49},\ldots\}\).
Although the quiz did not ask about monotonicity, bounded-ness, or convergence, we discussed them anyway. This sequence is strictly positive, that is to say: \(a_n \geq 0\) for all \(n\), so our sequence has a lower bound of zero. And, because the sequence is also monotone decreasing, the initial term must be the largest, so our sequence has both an upper and lower bound — therefore \(a_n\) is bounded.
Finally, because our sequence is both bounded and monotone, it must be convergent! We can see this explicitly by taking \(\displaystyle \lim_{n\to\infty} \frac{n+1}{2n^2-1} = 0\). This means that we can conclude that not only does \(a_n\) simply converge — but it specifically converges to zero.
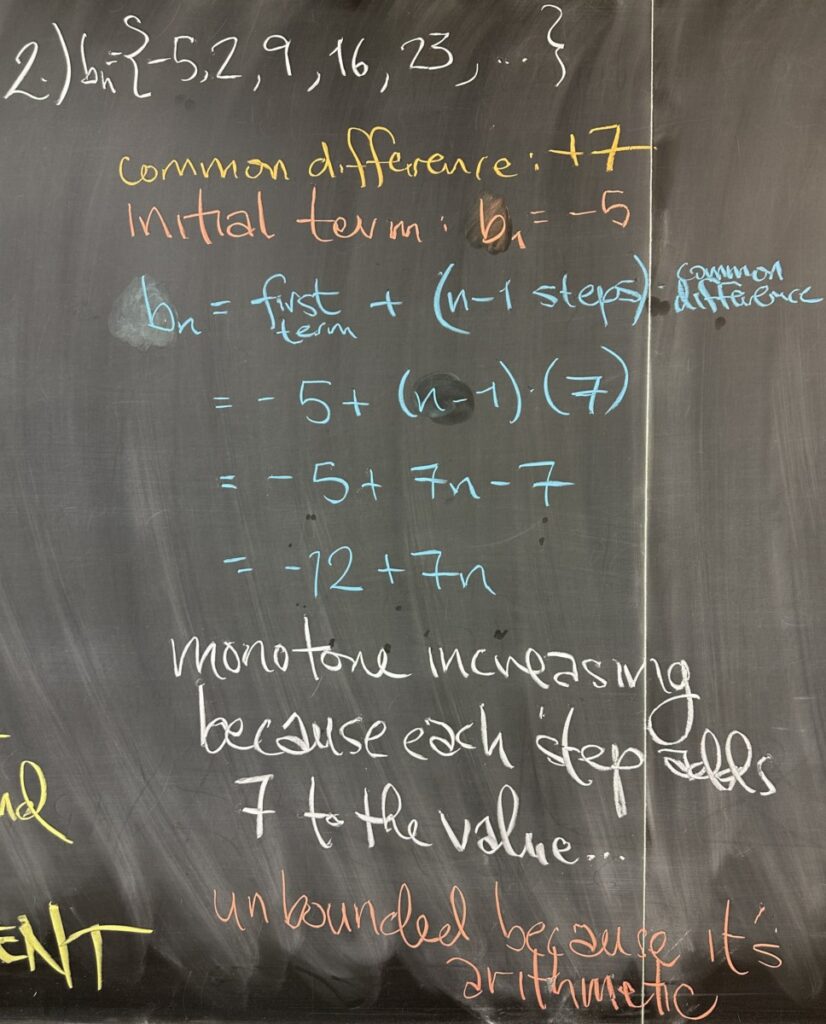
The second problem is reversed. Instead of providing the closed form for \(b_n\), the first five terms are given instead, and you were asked to give the closed form. From the given terms, \(\{-5,2,9,16,23,\ldots\}\), we should see that each term is seven more than its predecessor. In ‘proper’ terminology, this is a “common difference” — which tells us that this sequence is “arithmetic”.
Identifying this sequence as “arithmetic” helps us to construct the closed form (which is the initial term plus the common difference times one less than \(n\)). Explicitly, this looks like \(b_n = -5 + 7(n-1)\) as the closed form — which can be re-written in several different ways (but simplification is not required).
As an “arithmetic” sequence, \(b_n\) must be monotone (increasing if the common difference is positive, as we see here; or decreasing if the difference is negative) as well as unbounded (all arithmetic sequences).
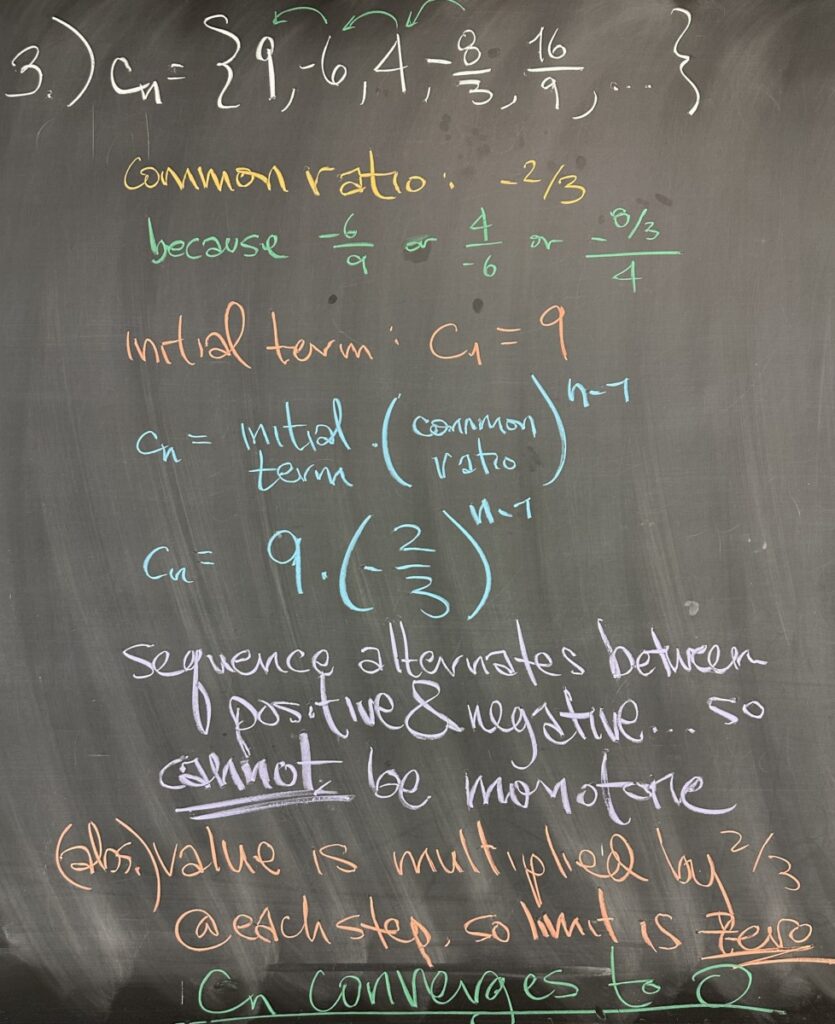
The third question also provides the first five terms and asks for the closed form for the sequence. This time, instead of a common difference, we see a common ratio between consecutive terms. For any pair of consecutive terms, we see the ratio of \(-\frac23\) in each case.
Sequences that have a common ratio are “geometric” — and they also have a template for the closed form: the initial term times the common ratio raised to the n-minus-one power. Specifically, this gives \(c_n = 9 \left(-\frac23\right)^{n-1}\).
Regarding classification of this sequence, we see that the terms ‘alternate’ back and forth between positive and negative values. This means it cannot be monotone, since every other step is an increase, then a decrease in value.
By looking at the absolute value of the common ratio and the absolute value of the values in the sequence, we see the values shrinking by a factor of \(\frac23\) at each step. Since this repeats at every step, both the positive and negative terms are trending towards zero as \(n\) continues to grow (\(n\to\infty\)). We conclude that this sequence converges to zero. Furthermore, any convergent sequence must be bounded.
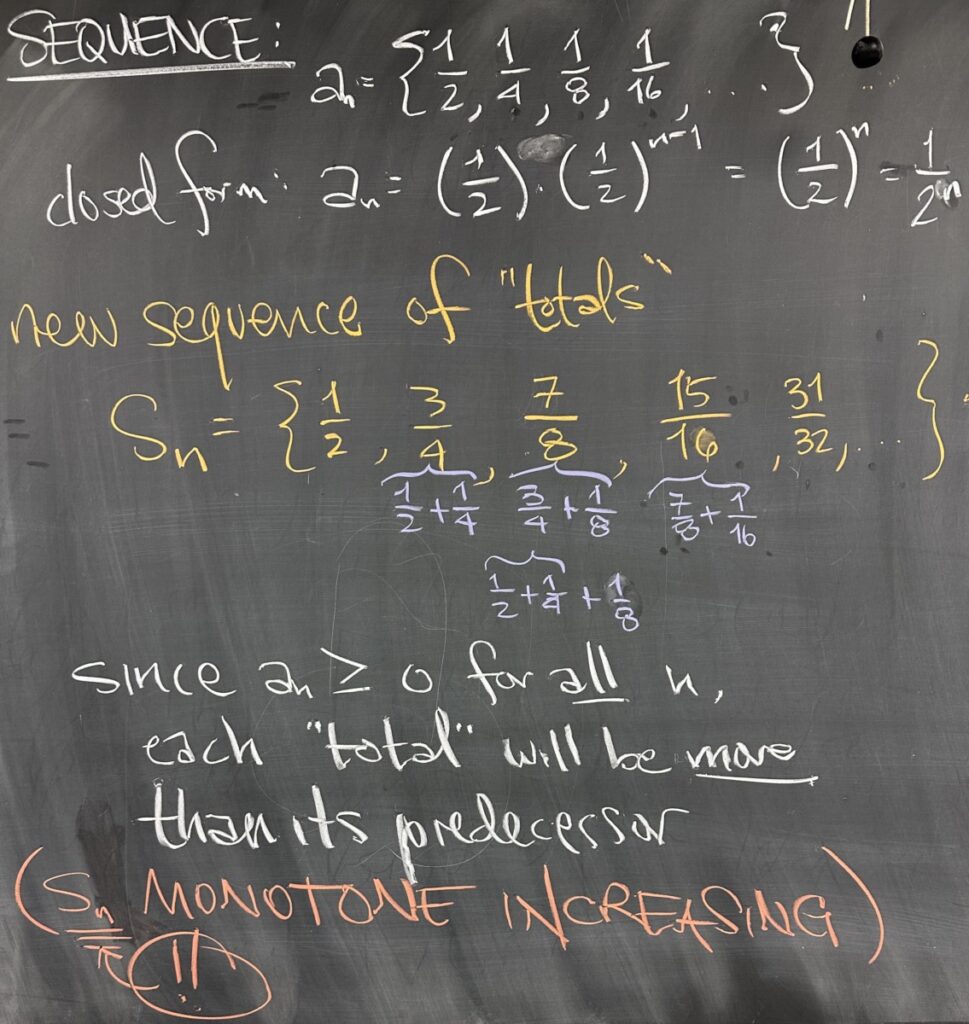
Sequences with closed forms are rather boring. If we have a closed form, then we can simply look at its limit to determine convergence. In our example from the previous lesson, \(a_n = \frac{1}{2^n}\), we can see that it has limit zero, is always positive, and also is monotone decreasing.
A more interesting situation arises when we shift to look at a new sequence which we construct from a sequence given by its closed form.
The new sequence is formed as a sum of terms from the original sequence. The first term of our new sequence is sum of the first term from the original sequence — it seems silly to say it that way — but \(s_1=\frac12\). The pattern for the new sequence becomes more clear as we proceed: \(s_2\) is the sum of the first two terms from the original sequence: \(s_2=\frac12+\frac14\). The third term is the sum of the first three terms from the original sequence: \(s_3 = \frac12+\frac14+\frac18\).
We can view this pattern recursively, as each term of the \(s_n\) sequence is the previous term \(s_{n-1}\) plus the next term of the original sequence, \(a_n\). This perspective reveals that the change from one term of \(s_n\) to the next is \(a_n\), and because (in this example) \(a_n > 0\) for all \(n\), we conclude that \(s_n\) is monotone increasing.
In fact, any time a sequence, (\(a_n\)), is strictly positive, its sequence of sums, (\(s_n\)), will be monotone increasing. Let’s be clear, these are two different sequences — the original, and the sums which are formed from it.
In this example, \(a_n = \{\frac12, \frac14, \frac18, \frac{1}{16}, \ldots\}\) is our original sequence. The (partial) sums formed from \(a_n\) is a new sequence: \(s_n = \{\frac12, \frac34, \frac78, \frac{15}{16}, \ldots\}\).

In our example, we have a closed form for \(a_n\), so convergence is determined by taking the limit of the closed form: \(\displaystyle\lim_{n\to\infty} \left(\frac12\right)^n = 0\). So \(a_n\) converges to zero.
It is not as straightforward for \(s_n\), although we “feel” that our values are trending towards one. In order to prove (or justify) this conclusion, we first find a closed form for \(s_n\). Looking at the pattern of values for \(s_n\), we see the denominator following the pattern \(2^n\), while the numerator is always one less than the denominator: \(s_n=\frac{2^n-1}{2^n}\).
If we can find the limit of this closed form, we can determine convergence.
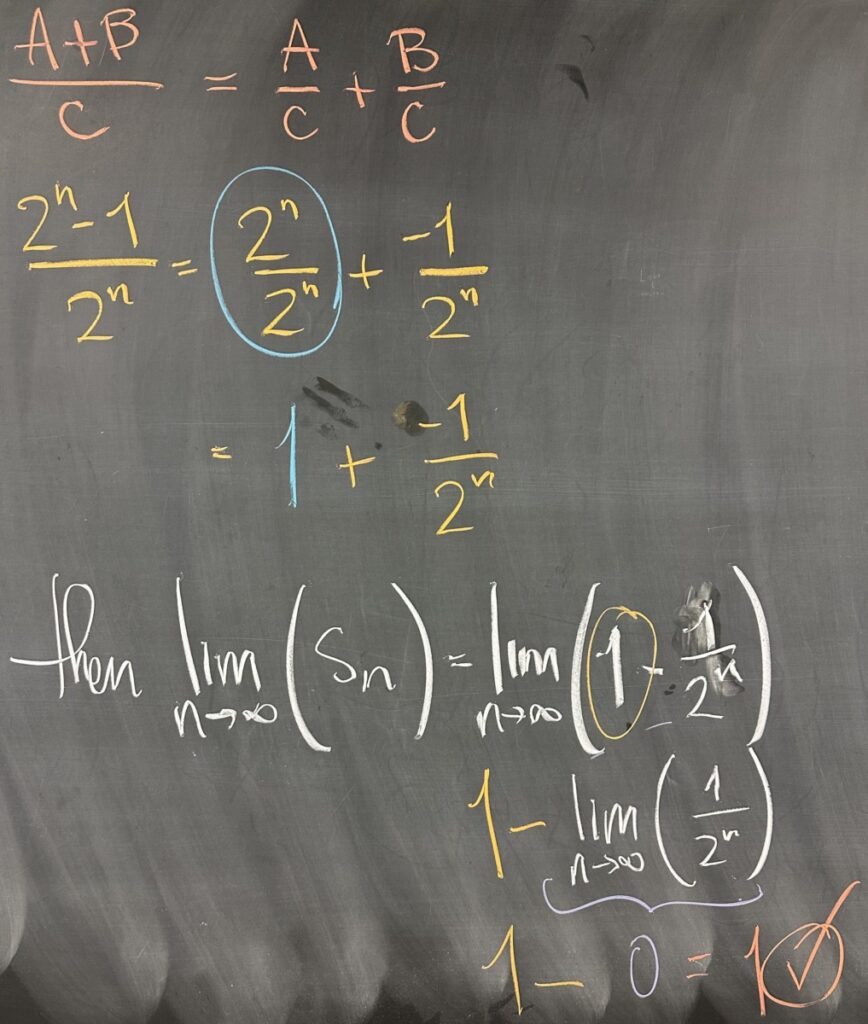
Using some algebra, we can rewrite the closed form for \(s_n\) in a way that makes the limit easier to compute: \(s_n=\frac{2^n-1}{2^n}=\frac{2^n}{2^n}-\frac{1}{2^n}\).
Recalling the linear properties of limits: \[\lim_{n\to\infty}\left(1-\frac{1}{2^n}\right)=\lim_{n\to\infty}\left(1\right)-\lim_{n\to\infty}\left(\frac{1}{2^n}\right)\]
Then \(\lim_{n\to\infty}1 = 1\) and \(\lim_{n\to\infty} \frac{1}{2^n} = 0\), so we can conclude that \(\lim_{n\to\infty} s_n=1\). This is proof (justification) that our sequence of sums converges to one.

We will be using this construction for a sequence of partial sums for the next several weeks, so we outline it here.
First, we have a sequence (in closed form) to start with: \(a_n=f(n)\).
From this sequence, our sequence of partial sums is constructed without a closed form. Note that certain sequences (geometric) will have a closed form (as we saw in the previous example), but most will not.
Our goal will be to determine whether or not the sequence of partial sums converges. Recall that a sequence is said to “converge” if it “has a limit as \(n\to\infty\)”.
If this limit exists, it is called the “infinite sum” of \(a_n\).
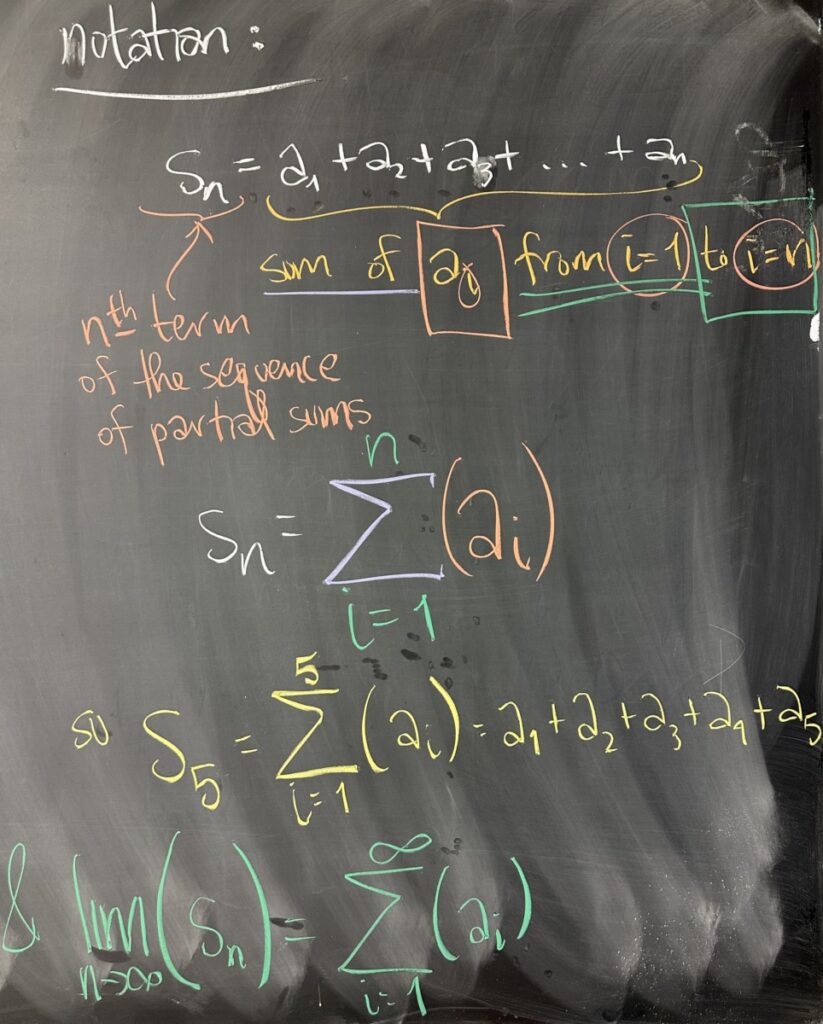
Because we will be considering this sequence of partial sums so often, we have some notation to learn.
The \(n^\text{th}\) term of the sequence of partial sums is the sum of the first \(n\) terms of \(a_i\). Note that \(n\) here is being used specifically to refer to which step of the partial sum sequence that we are on — so we cannot re-use \(n\) when talking about the \(a\) sequence — and that is why we use \(a_i\) with \(i\) instead of \(n\).
In order to abbreviate \(s_n=a_1+a_2+a_3+\ldots+a_n\), we write \[s_n=\sum_{i=1}^n\left(a_i\right)\]
And in referring to the “infinite sum” (if it exists), we write \[\lim_{n\to\infty}\left(s_n\right)=\sum_{i=1}^\infty\left(a_i\right)\]




Recent Comments