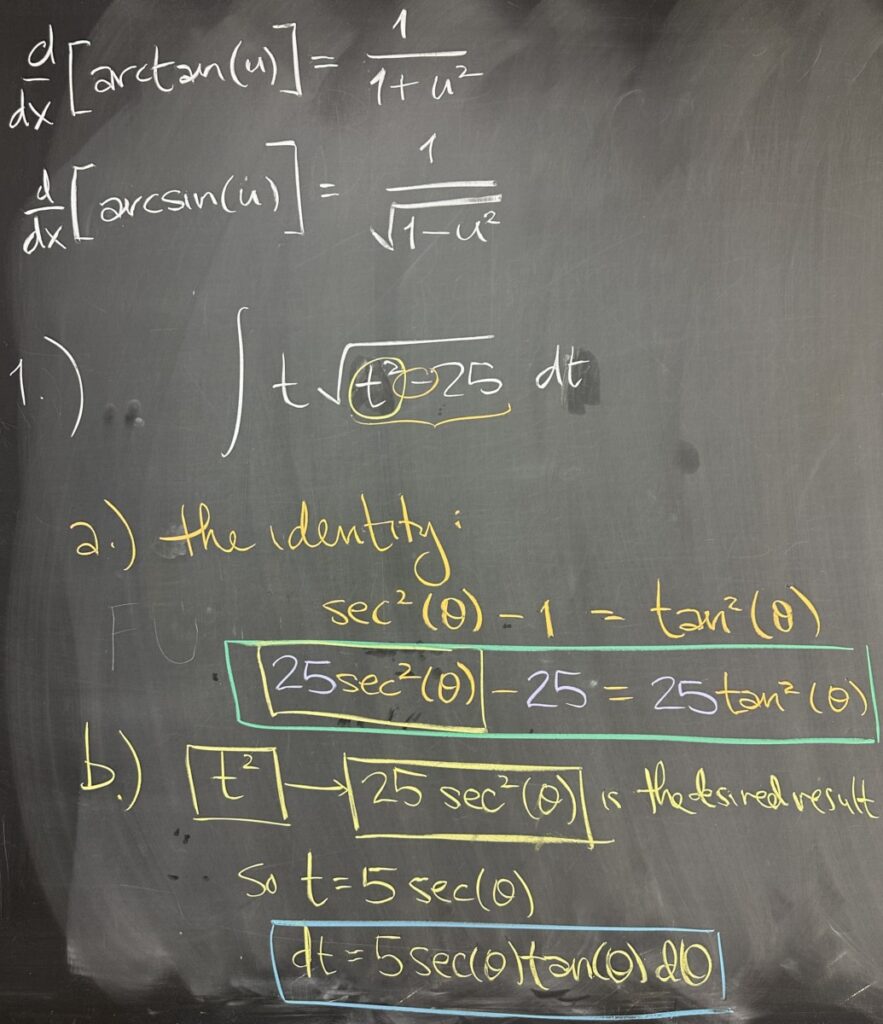
Today’s quiz walks through the trig substitution approach to integrating \(\int t\sqrt{t^2-25}\,dt\). The first step in trig substitution is to identify the relevant pythagorean identity — here we see \(t^2-25\), where the constant is subtracted from \(t^2\). The identity with this pattern is \(\sec^2(\theta)-1=\tan^2(\theta)\), and in order to get \(25\) as the subtracted value, we multiply through to get \(25\sec^2(\theta)-25=25\tan^2(\theta)\).
So, with this identity in mind, we want to swap our \(t^2\) for \(25\sec^2(\theta)\), which means we must substitute \(t=5\sec(\theta)\). We must also substitute the differential, \(dt=5\sec(\theta)\tan(\theta)\,d\theta\).

It’s time to make the substitution: \[\int t\sqrt{t^2-25}\,dt=\int 5\sec(\theta)\textcolor{purple}{\sqrt{25\sec^2(\theta)-25}}\cdot 5\sec(\theta)\tan(\theta)\,d\theta\]
After substituting, we want to use the trig identity that we’ve set up for:\[\sqrt{25\sec^2(\theta)-25}=\sqrt{25\tan^2(\theta)}=5\tan(\theta)\]
This reduces our integral to:\[\int 5\sec(\theta)\cdot\textcolor{purple}{5\tan(\theta)}\cdot 5\sec(\theta)\tan(\theta)\,d\theta=125\int\tan^2(\theta)\sec^2(\theta)\,d\theta\]
We consider both of the apparent u-substitutions, either \(u=\sec(\theta)\) or \(u=\tan(\theta)\). The differential for substituting \(u=\sec(\theta)\) would leave us with an un-substituted \(\tan(\theta)\) — not to mention, this substitution would effectively reverse the trig substitution we just made (which would put the integral roughly back where we started).
The substitution \(u=\tan(\theta)\) has differential \(du=\sec^2(\theta)\,d\theta\), which leaves the integral: \[125\int\tan^2(\theta)\textcolor{darkblue}{\sec^2(\theta)\,d\theta}=125\int u^2\textcolor{darkblue}{du}\]
This is now a pretty straightforward antiderivative: \(125\int u^2\,du=\frac{125}{3}u^3+C\). Then we unwind our u-substitution: \(\frac{125}{3}\tan^3(\theta)+C\)
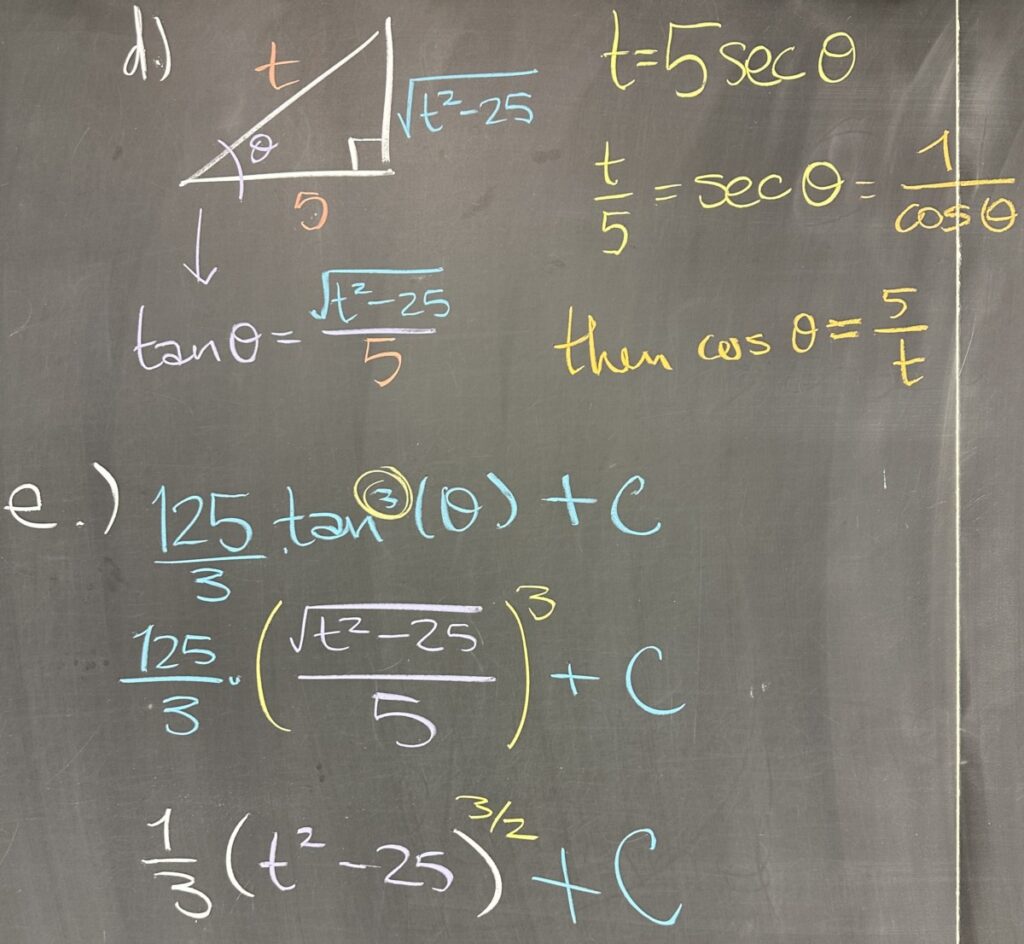
Our final steps for trig substitution are geared towards converting the \(\tan(\theta)\) from our antiderivative into a function of our original variable \(t\).
Our original trig substitution was \(t=5\sec(\theta)\), from which we can see that \(\sec(\theta)=\frac{t}{5}\). Since secant is the reciprocal of cosine, this is equivalent to \(\cos(\theta)=\frac{5}{t}\). Whether we consider the secant ratio or the cosine ratio, in both cases we see that the hypotenuse is \(t\) and the adjacent leg is \(5\). The pythagorean theorem helps us find the opposite leg: \(\sqrt{t^2-25}\).
Now we can convert our \(\tan(\theta)=\frac{\sqrt{t^2-25}}{5}\) in the antiderivative to get:\[\frac{125}{3}\left(\tan(\theta)\right)^3+C=\frac{125}{3}\left(\frac{\sqrt{t^2-25}}{5}\right)^3+C\]
We can simplify this expression: \(\frac13(t^2-25)^\frac32+C\)

Today’s topic is all about fractions, so we start with some review of how arithmetic works with fractions. Adding fractions requires converting each summand to a common denominator before adding the numerators.
What we are interested in today is a process called “decomposition.” This process is all about taking a fraction (one that doesn’t reduce) and splitting it into pieces that do reduce.
For example, \(\frac34=\frac24+\frac14=\frac12+\frac14\). Or, with \(\frac78=\frac48+\frac28+\frac18=\frac12+\frac14+\frac18\). In both of these examples, we started with a fraction that doesn’t reduce, but there are smaller pieces of the total fraction that would reduce.
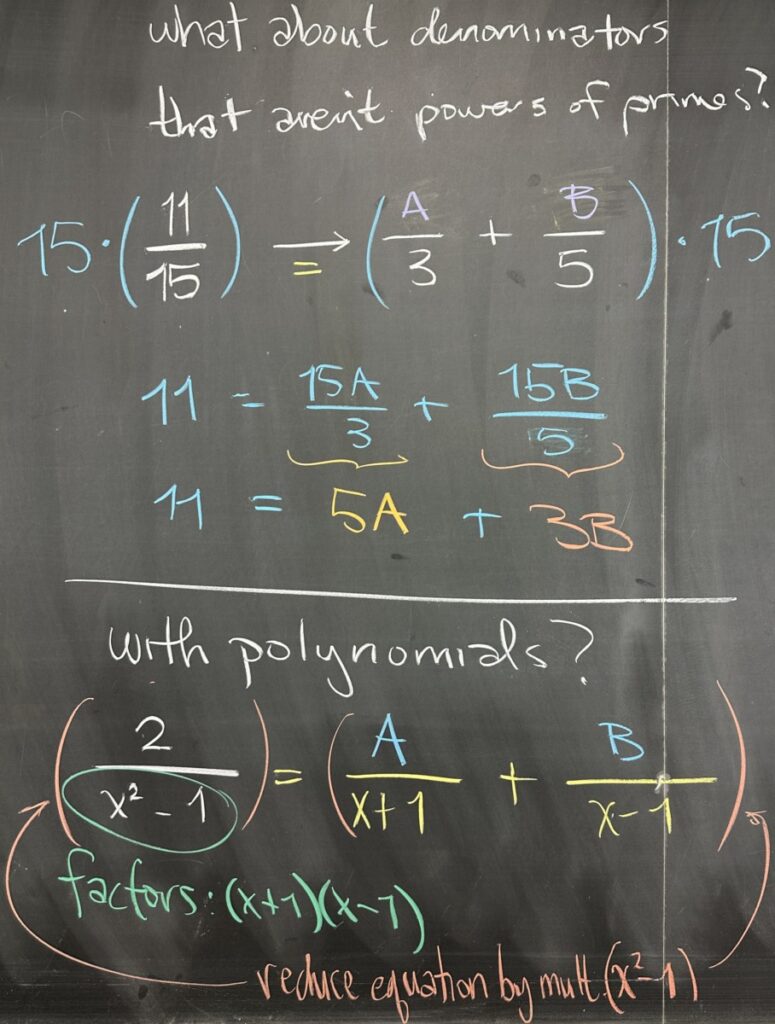
In our two examples, we had denominators that were powers of primes (\(2^2\) and \(2^3\)), what about fractions that are products of different primes? For example, \(\frac{11}{15}\) might have pieces that reduce to thirds or fifths. We might do some guess-and-check to decompose \(\frac{11}{15}\), but we want to develop a strategy for this decomposition process.
We expect our fifteenths to decompose into fifths and thirds, so we can express this as \(\frac{11}{15}=\frac{A}{3}+\frac{B}{5}\). It’s easier to solve an equation like this without denominators — so we multiply through by \(15\) and end up with \[11=\frac{15A}{3}+\frac{15B}{5}=5A+3B\]
This isn’t enough for us to determine unique values for \(A\) and \(B\) (in fact, there aren’t unique solutions here, e.g. \(A=1, B=2\) and \(A=4, B=-3\) are both solutions). However, this is the process we will follow when decomposing fractions of polynomials. Let’s take a look at an example of a polynomial fraction.
Let’s consider the fraction \(\frac{2}{x^2-1}\). The denominator is a product (as before, when we had \(15=3\cdot 5\)), so we would like to express it as a sum of ‘simpler’ fractions. \(x^2-1\) is the product \((x+1)(x-1)\), so we hope to decompose \(\frac{2}{x^2-1}=\frac{A}{x+1}+\frac{B}{x-1}\).
Similar to our previous examples, this equation will be easier to work with if we multiply through by the least common denominator: \(x^2-1\).
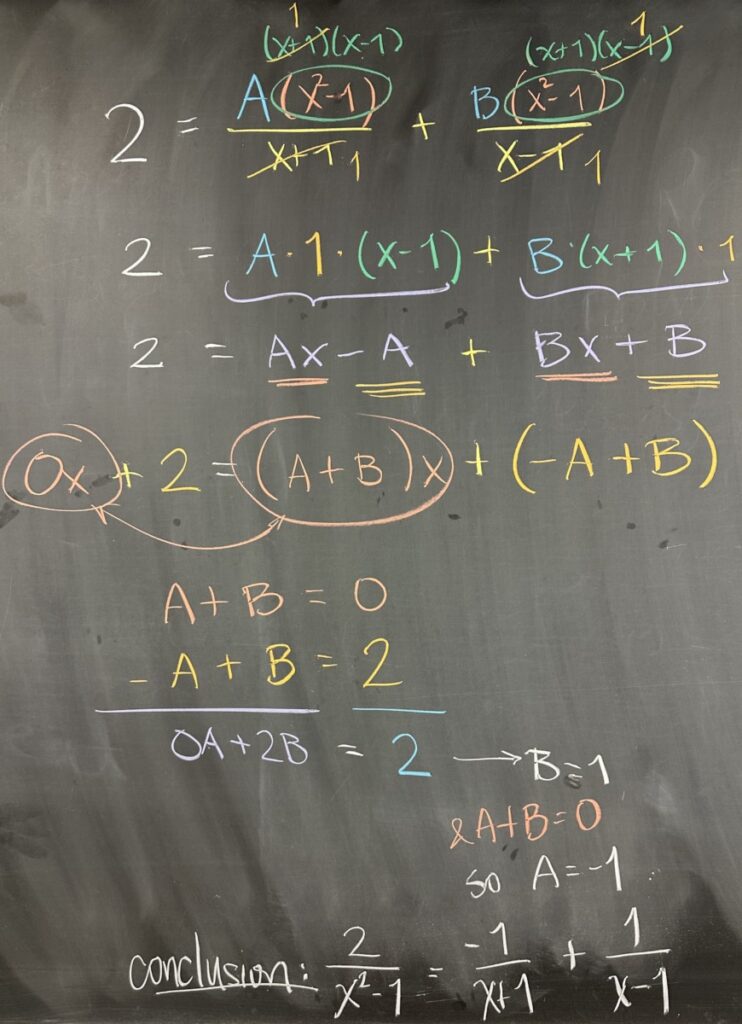
After multiplying the equation \(\frac{2}{x^2-1}=\frac{A}{x+1}+\frac{B}{x-1}\) through by \(x^2-1\), we need to reduce: \[\frac{2\textcolor{darkgreen}{(x^2-1)}}{\textcolor{darkgreen}{x^2-1}}=\frac{A(x^2-1)}{x+1}+\frac{B(x^2-1)}{x-1}\]
Recall that \(x^2-1\) factors into the product \((x+1)(x-1)\): \[2=\frac{A\textcolor{darkgreen}{(x+1)}(x-1)}{\textcolor{darkgreen}{x+1}}+\frac{B(x+1)\textcolor{darkgreen}{(x-1)}}{\textcolor{darkgreen}{x-1}}\]
And we finally end up with \[2=A(x-1)+B(x+1)\]
So, when distributed: \[\textcolor{darkred}{0x}+2=Ax-A+Bx+B\]
And because like terms do not interact with un-like terms, we see that \(0x=Ax+Bx\), so \(0=A+B\); and that \(2= -A+B\). These two equations (in \(A\) and \(B\)) form a system of equations that can be solved using substitution or elimination methods.
In class, we used the elimination method to determine that \(B=1\) and then, since \(A+B=0\), we see that \(A=-1\).
This concludes our decomposition: \[\frac{2}{x^2-1}=\frac{-1}{x+1}+\frac{1}{x-1}\]
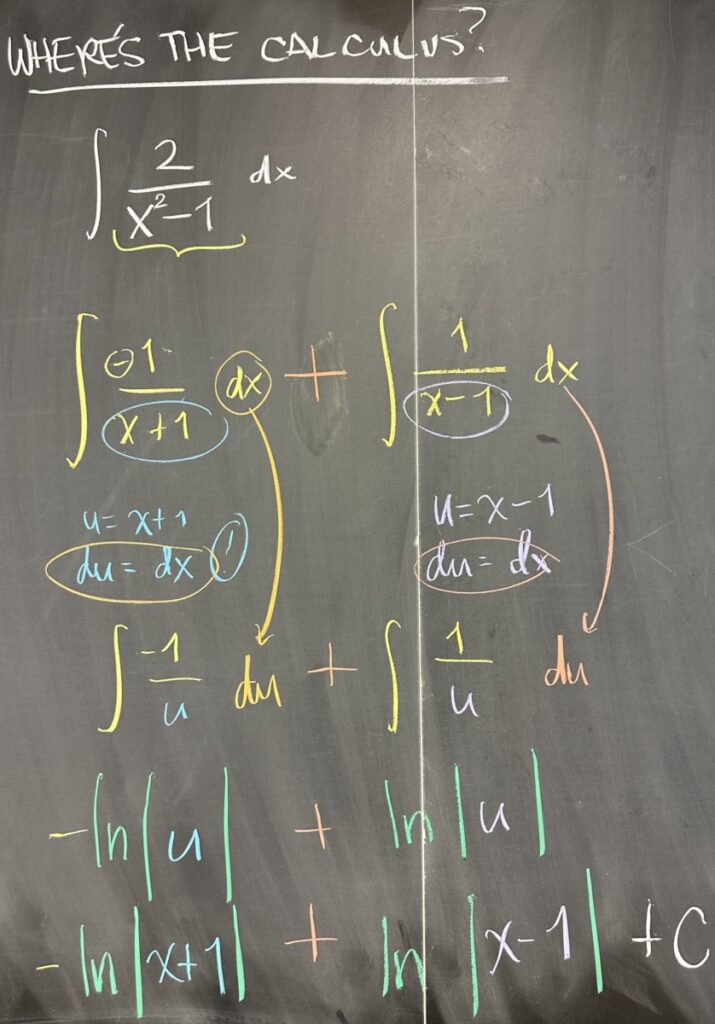
So what does all this have to do with Calculus? Decomposition of fractions looks like purely an algebraic exercise!
Well, what if we were to try to integrate \(\int\frac{2}{x^2-1}\,dx\)? This integral is not one that we cannot handle with our existing techniques — but using decomposition, we can rewrite it:\[\int\frac{2}{x^2-1}\,dx=\int\frac{-1}{x+1}\,dx+\int\frac{1}{x-1}\,dx\]
We have substitutions we can make in each of these separate integrals: \(u=x+1\) in the first integral, and \(u=x-1\) in the second.
- \(\int\frac{-1}{x+1}\,dx=-\int\frac{1}{u}\,du=-\ln|u|=-\ln|x+1|\)
- \(int\frac{1}{x-1}\,dx=\int\frac{1}{u}\,du=\ln|u|=\ln|x-1|\)
So, we conclude that our integral is: \[\int\frac{2}{x^2-1}\,dx=-\ln|x+1|+\ln|x-1|+C\]
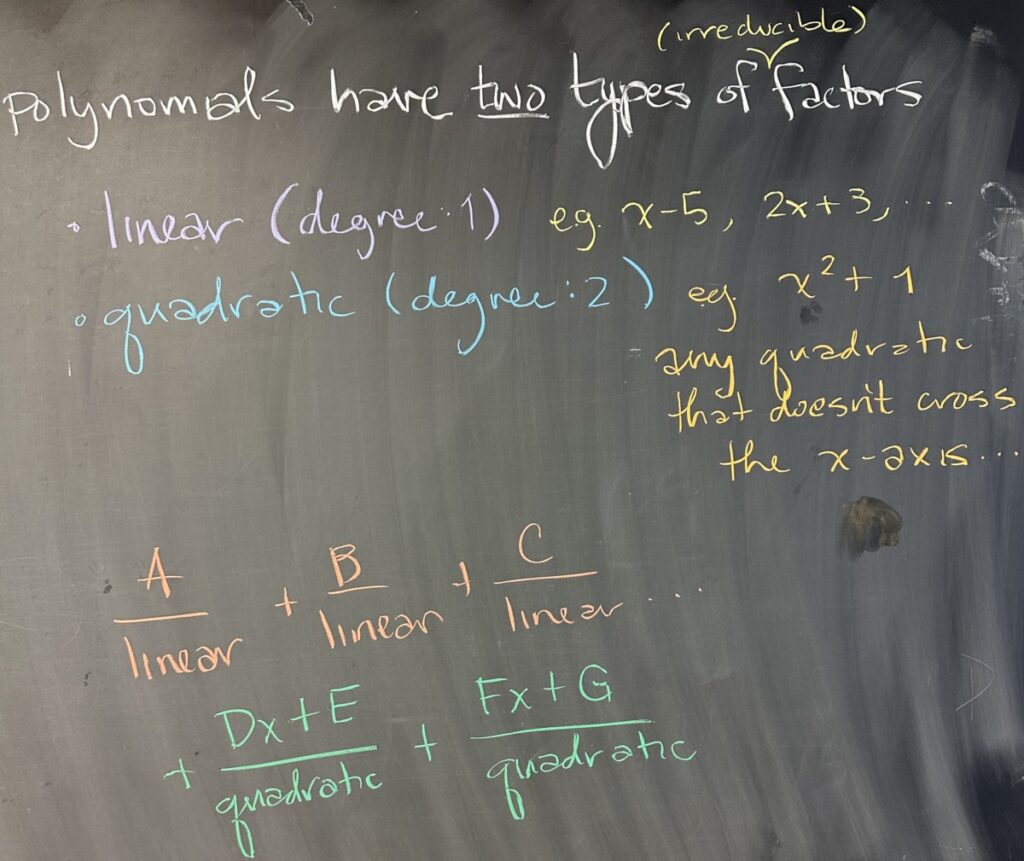
In general, polynomials have only two types of (irreducible) factors. There are linear factors (they have degree 1, like any \(mx+b\), i.e. lines), and there are irreducible quadratic factors (they have degree 2, and cannot be written as a product of linear factors).
- Linear factors are those like \(x-4\), or \(2x+5\), or \(-x-9\)…
- Irreducible quadratic factors are those like \(x^2+1\), or \((x-1)^2+4=x^2-2x+5\) — those quadratics that have graphs that don’t cross the \(x\)-axis
In class we talked about how parabolas are quadratics, and those that don’t cross the \(x\)-axis don’t have roots (x-intercepts). And since each root corresponds to a factor, those without roots are exactly those that do not factor (are irreducible).
When decomposing polynomial fractions, we require that the numerator have smaller degree than the denominator. This means that linear factors have just a constant numerator (like \(A\)), and quadratic factors have linear numerators (like \(Ax+B\)).




Recent Comments