
Jumping right into the action today, remember that we are studying series, which are built from sequences. Sequences are given in closed form, and our series typically do not have a closed form available. Our question is always “does this series converge or diverge?”
Last lecture, we covered the Direct Comparison Test (DCT). This test only applies to positive series (constructed from positive sequences). This test relies on “direct” comparison of two series — meaning that one of the sequences is always larger than the other. This notion transfers to the series, as adding up values from the larger sequence will always result in a larger partial sum than adding values from the smaller sequence.
Furthermore, since the sequences are always positive, their partial sums must be increasing (monotone).
It can be useful to visualize these monotone series (sequence of partial sums) as a curve that slopes upwards. The DCT tells us that if the smaller of the two series diverges (is unbounded), then that forces the larger series to also be unbounded (since it is always larger).
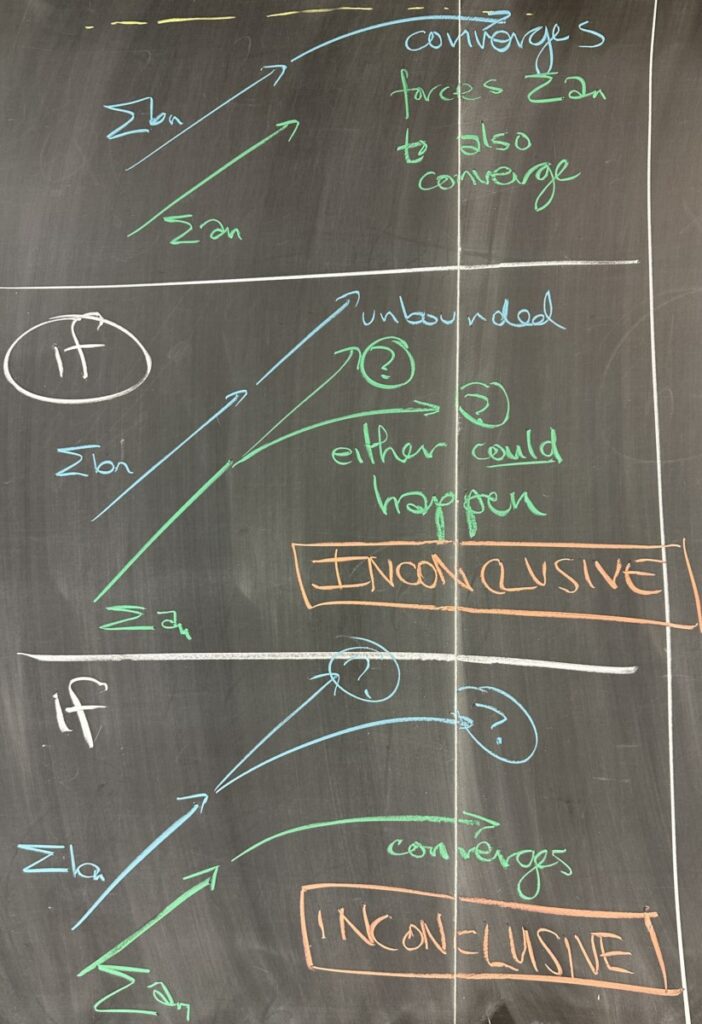
The DCT also says that if the larger of the two series converges (the partial sums have asymptotic behavior), then the smaller series cannot be unbounded (since it must remain smaller) and must therefore converge also.
The unfortunate thing is that the DCT is inconclusive in two cases: when the larger series is unbounded; and when then smaller series converges.

Here’s a bit of advice on using the DCT — all of our problems will be questions about the convergence of a series. This series has a sequence with a closed form: \(a_n = f(n)\), and we will want to use the DCT to shift our focus to a simpler closed form: \(b_n = g(n)\). For the DCT, we just hope that \(g(n)\) makes one of the conclusive combinations with \(f(n)\).
Let’s now look at two different examples — one that works with DCT, and then one that does not (despite being very similar to the first).
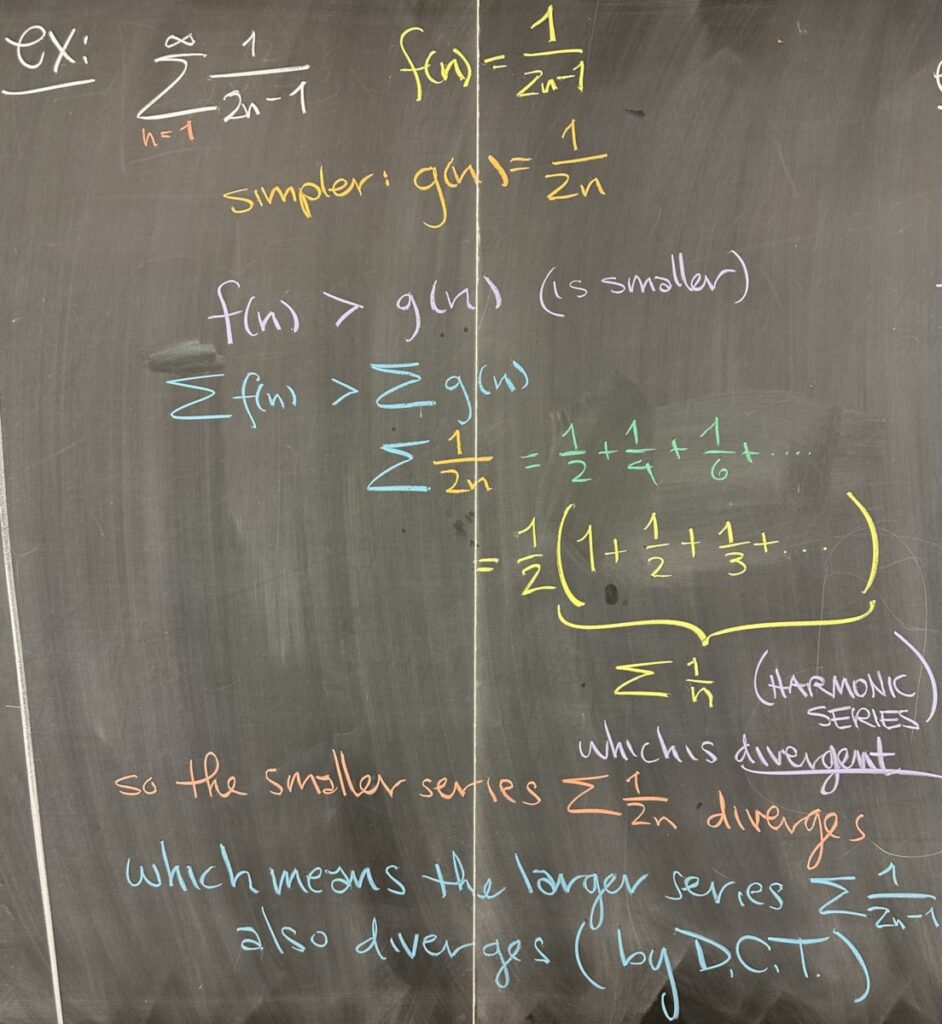
In our first example, \(f(n)=\frac{1}{2n-1}\). A simpler version of this closed form would be \(g(n)=\frac{1}{2n}\). In direct comparison, we see that \(f(n)>g(n)\) for all values of \(n\) — and this extends to the series as well: \(\sum f(n) > \sum g(n)\).
So, we’d like to determine whether our \(\sum g(n)\) series converges or diverges. When we don’t know what else to do, it can be useful to look at the specific values — in this case, \(sum \frac{1}{2n}=\frac12+\frac14+\frac16+\ldots\). This is exactly half of the harmonic series, which is divergent (even half of an unbounded series will still be unbounded).
In this example, we were fortunate. Our original series, \(\sum\frac{1}{2n-1}\), is larger than a divergent series, \(\sum\frac{1}{2n}\); so the DCT allows us to conclude that \(\sum\frac{1}{2n-1}\) is also divergent.
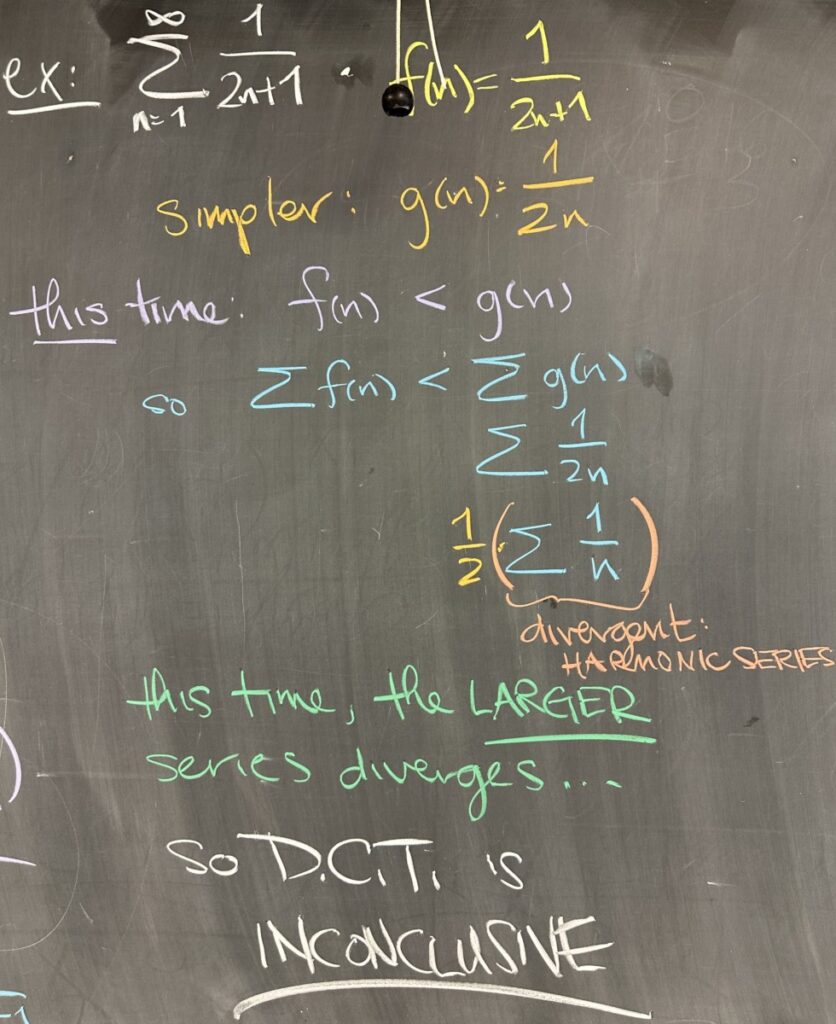
The next example is very similar to the previous one: \(\sum\frac{1}{2n+1}\). With the closed form \(f(n)=\frac{1}{2n+1}\), the simpler version would again be \(g(n)=\frac{1}{2n}\). This time, however, in direct comparison, we see that \(f(n)<g(n)\) for all \(n\) (which also extends to the series). The \(\sum g(n)\) series is again half of the harmonic series, \(\frac12\sum\frac1n\), which diverges.
The direct comparison is the wrong way to be conclusive — our original series \(\sum\frac{1}{2n+1}\) is smaller than a divergent series. And under these conditions, the DCT is inconclusive.

Before we get to an “improved” version of the comparison test, we pause to consider a new category of series: the p-series. This category of series have sequences with the closed form \(f(n)=\frac{1}{n^p}\) with \(p>0\).
Note that for all of these sequences (not the series), they all converge to zero. And because the sequence values are all positive, the series (partial sums) are monotone increasing.
The nice thing is that we can always determine the convergence of any p-series. If \(p\leq 1\), the series \(\sum\frac{1}{n^p}\) diverges. And if \(p>1\), the series \(\sum\frac{1}{n^p}\) converges. These conclusions are known as the p-series test (PST).
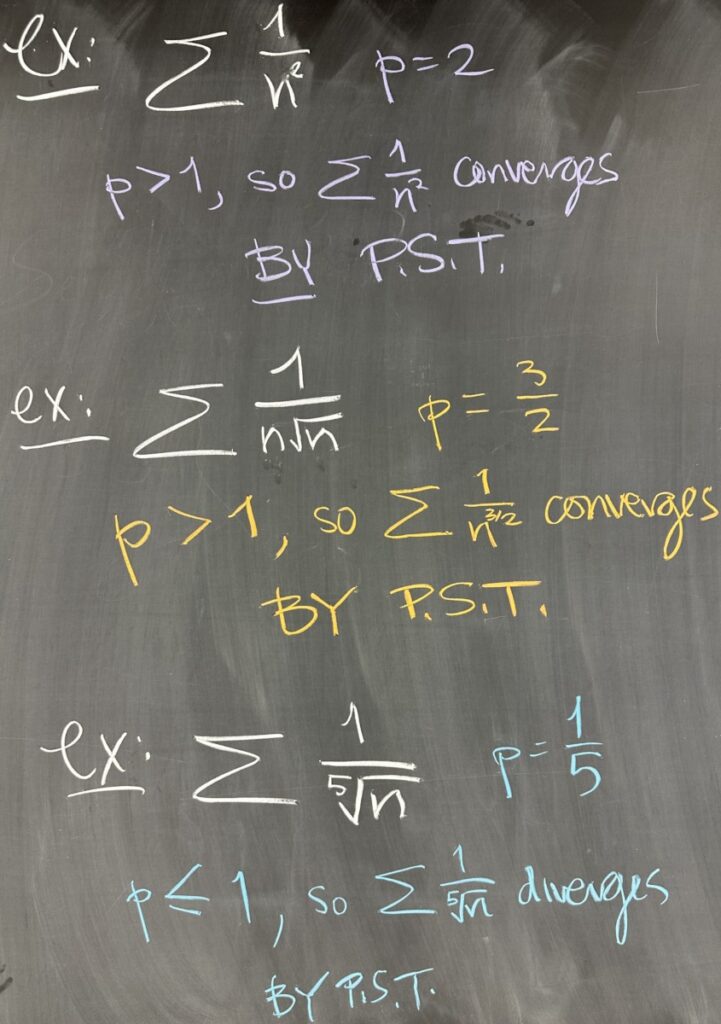
These are some rapid-fire examples, all of them are p-series.
\(\sum\frac{1}{n^2}\) is a p-series with \(p=2\). Since \(p>1\), we conclude that the series converges by PST.
\(\sum\frac{1}{n\sqrt{n}\) is a p-series with \(p=\frac32\). Since \(p>1\), we again conclude that the series converges by PST.
\(\sum\frac{1}{\sqrt[5]{n}}\) is a p-series with \(p=\frac15\). Since \(p\leq1\), we conclude that the series diverges by PST.
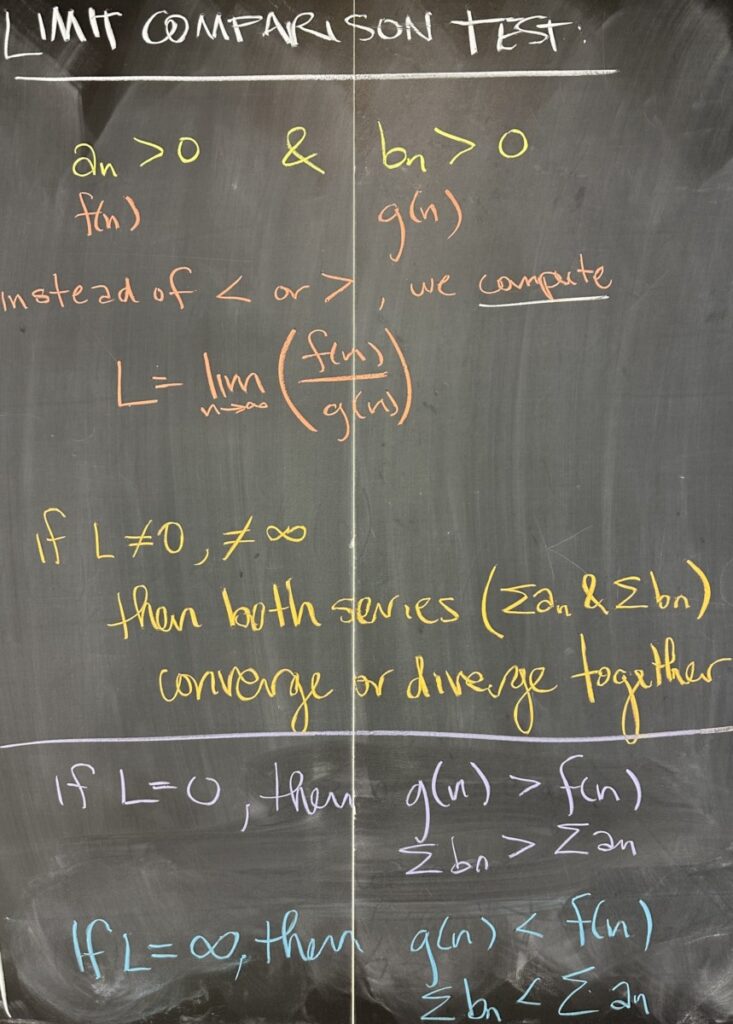
Now we move on to talk about the “improved” comparison test, called the Limit Comparison Test (LCT). Similar to the DCT, we again have two series to compare, and both must be constructed from positive sequences (\(a_n>0\) and \(b_n>0\)). Instead of comparing them directly (to see which is larger or smaller), we consider the limit: \[L=\lim_{n\to\infty}\left(\frac{a_n}{b_n}\right)\]
If this \(L\) is a finite, non-zero number, then both series (\(a_n>0\) and \(b_n>0\)) either converge or diverge together. (This is much better than the DCT, since all combinations are conclusive.)
The book adds to the LCT in a way that I don’t particularly prefer — but I discussed a version of their argument anyhow. If \(L=0\), the LCT is “inconclusive”, but DCT can be used with the understanding that \(\sum b_n\) (the series corresponding to the denominator from our limit) is greater than \(\sum a_n\). Alternatively, if \(L=\infty\), the LCT is again “inconclusive”, but DCT can be used with \(\sum a_n\) greater than \(\sum b_n\).
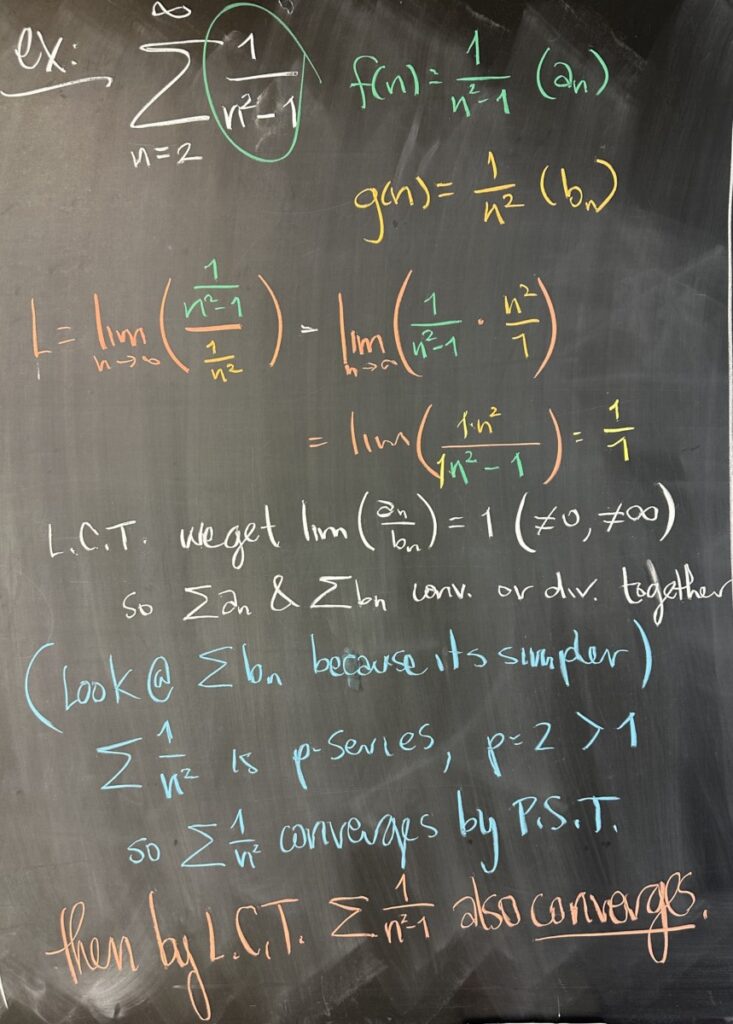
In this next example, we apply the LCT to \(\sum\frac{1}{n^2-1}\). With \(f(n)=\frac{1}{n^2-1}\), the simplified form is \(g(n)=\frac{1}{n^2}\). This time, it is irrelevant which is larger, since we will be considering the limit: \[L=\lim_{n\to\infty}\left(\frac{\frac{1}{n^2-1}}{\frac{1}{n^2}}\right)\]
We’ll be handling limits like these pretty much every time we apply the LCT, so get used to dividing fractions: \[\frac{\frac{1}{n^2-1}}{\frac{1}{n^2}}=\frac{1}{n^2-1}\cdot\frac{n^2}{1}=\frac{n^2}{n^2-1}\]
This fraction has limit \(1\), which is a finite, non-zero number — so the LCT tells us that \(\sum a_n\) and \(\sum b_n\) either converge or diverge together.
Since \(\sum b_n\) is the simpler of the two (it’s a p-series), we are able to determine it’s convergence/divergence first. Since \(\sum\frac{1}{n^2}\) is a p-series, with \(p=2\), which is greater than \(1\) — so \(\sum\frac{1}{n^2}\) converges by PST.
Finally, we are able to conclude that \(\sum a_n=\sum\frac{1}{n^2-1}\) converges by LCT.
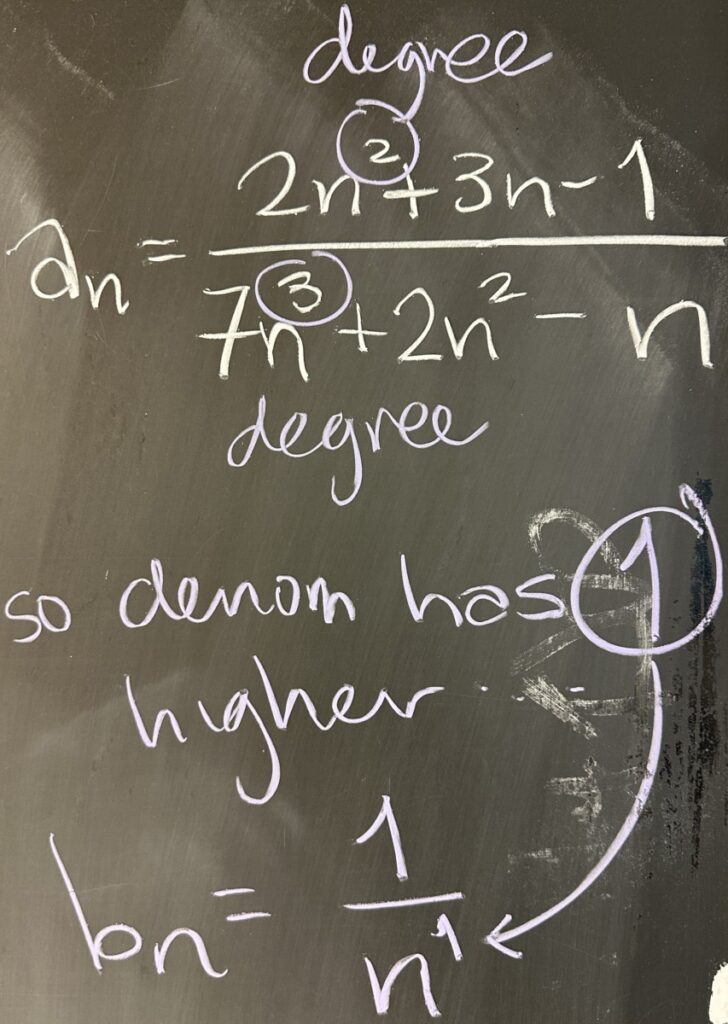
In general, when applying LCT to an \(a_n\ that is a rational function (a fraction of polynomials), determining a “good” \(b_n\) can by done by measuring the difference between the degrees of the numerator and denominator of \(a_n\).
In this example, \(\sum\frac{2n^2+3n-1}{7n^3+2n^2-n}\), we have a degree \(2\) polynomial in the numerator, and a degree \(3\) polynomial in the denominator (a difference of \(1\) in their degrees). This indicates that our best choice for \(b_n\) is \(\frac{1}{n^1}\).
Then the fraction \(\frac{a_n}{b_n}\) simplifies: \[\frac{\frac{2n^2+3n-1}{7n^3+2n^2-n}}{\frac1n}=\frac{2n^2+3n-1}{7n^3+2n^2-n}\cdot\frac{n}{1}\]

This fraction will have the same degree in the numerator and denominator, so there will be a finite, non-zero limit.
This will happen every time we select \(b_n\) to be a p-series with \(p\) equal to the difference in degrees from the numerator and denominator of \(a_n\).




Recent Comments