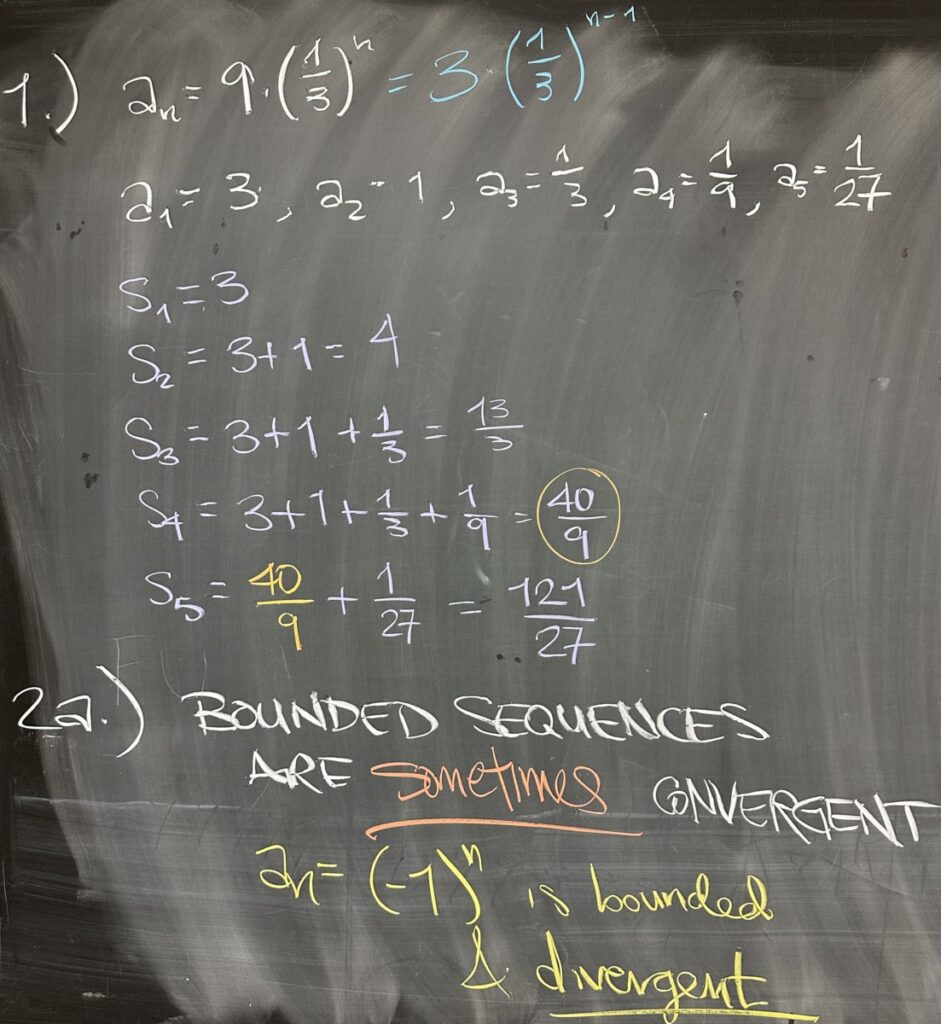
The first problem on today’s quiz asked for the first five terms of the sequence of partial sums. Keep in mind that the sequence of partial sums is computed from the given sequence… so we will need \(a_1,a_2,a_3,a_4\), and \(a_5\) first.
Once we have the first five terms of \(a_n\), we can compute the partial sums. \(s_1\) is the sum of the first “one” terms — so \(s_1\) is the same as \(a_1\). \(s_2=3+1=4\). We went on to compute \(s_3=\frac{13}{3}\), \(s_4=\frac{40}{9}\), and finally \(s_5=\frac{121}{27}\).
The second problem on the quiz presented four different statements and asked whether or not each statement was “sometimes” true, “always” true, or “never” true.
The first statement: “bounded sequences are convergent”, is sometimes true. We have already seen several examples of bounded sequences that are convergent — but there are also bounded sequences that are divergent. Here I provided an example: \(a_n=(-1)^n\), which is bounded and divergent. This sequence never gets larger than one, and is never less than negative one.

The second statement: “unbounded sequences are convergent”, is never true. In order to be “unbounded”, the sequence must continue to exceed every possible upper bound (or every possible lower bound). As such, the values appearing in the sequence must be trending towards infinity, negative infinity, or possibly both (consider a sequence like \(a_n=(-2)^n\)).
The third statement: “convergent sequences are bounded”, is always true. Because the sequence is convergent, its “tail” must be approaching (hence very close) to a single value (its limit). This prevents the sequence from trending towards infinity or negative infinity (which is necessary in order to be “unbounded”).
The final statement “convergent sequences are unbounded”, is never true. See the reasoning from the third statement.
In moving towards our topic for today, we consider the sequence from the first quiz problem: \(a_n=9(\frac13)^n\). Because the common ratio is less than one, we conclude that the limit of the sequence is zero (that is to say, \(a_n\) converges to zero). But what about the sequence of partial sums, what can be said about it? Since \(a_n>0\) for all \(n\), we know that \(s_n\) is monotone increasing — but is it bounded (which would tell us that \(s_n\) converges)? We may have a feeling that this is true — but we don’t have the tools to prove it yet!

First, we introduce the term “series” to refer to any sequence of partial sums (that’s a mouthful, so it’s easier to just call them “series”). When we call a series “geometric”, we mean to say that it is the sequence of partial sums for a geometric sequence.
Every geometric sequence is determined by its first term, \(a_1\), and the common ratio, \(r\). If we construct a geometric series from a geometric sequence, we have that \(s_n=a_1+a_1r+a_1r^2+\ldots+a_1r^{n-1}\). Note here that this is not a closed form, since the number of terms changes depending on the value of \(n\).
Using a clever algebra trick, we consider \(r\cdot s_n=a_1ra_1r^2+a_1r^3+\ldots+a_1r^n\), which we subtract from \(s_n\). This creates a lot of “like terms” which reduce to zero — leaving only \(s_n-s_nr=a_1-a_1r^n\). Solving this equation for \(s_n\), we get a closed form: \[s_n=\frac{a_1(1-r^n)}{1-r}\]
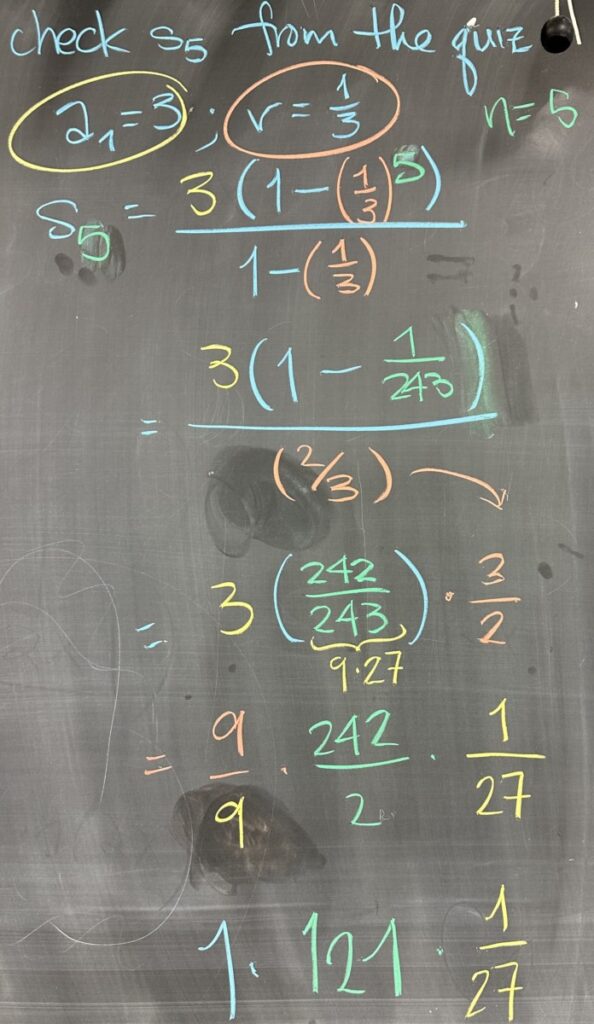
We can validate this closed form for the \(n^\text{th}\) term of the geometric series by computing \(s_5\) using the initial term and common ratio from our first quiz problem (we should end up with the same result: \(s_5=\frac{121}{27}\). It takes a fair bit of arithmetic, but we conclude that \[s_5=\frac{3(1-(\frac13)^5)}{1-\frac13}=\frac{121}{27}\]
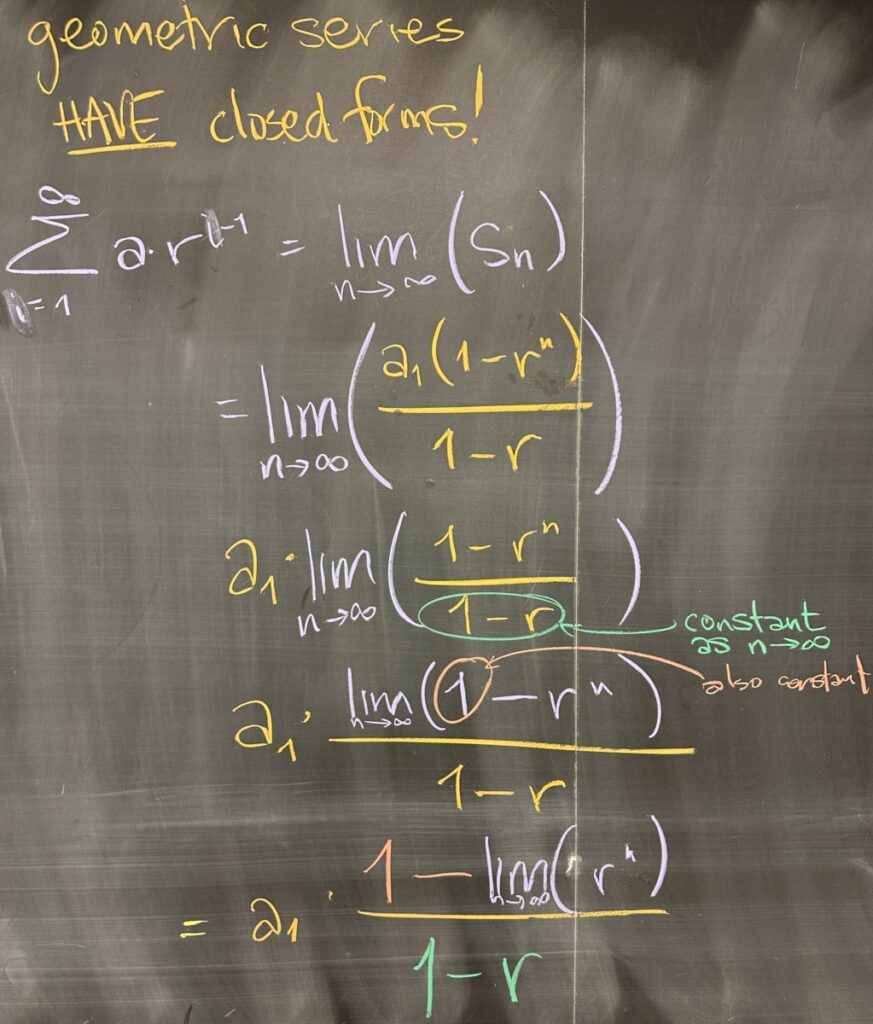
So, now we have a closed form for every geometric series, so \(\displaystyle\lim_{n\to\infty}\left(\frac{a_1(1-r^n}{1-r}\right)\) would give us the value for the infinite sum, if it exists.
Using properties of limits, we see that the limit simplifies to \(\displaystyle a_1\left(\frac{1-\lim_{n\to\infty}(r^n)}{1-r}\right)\).
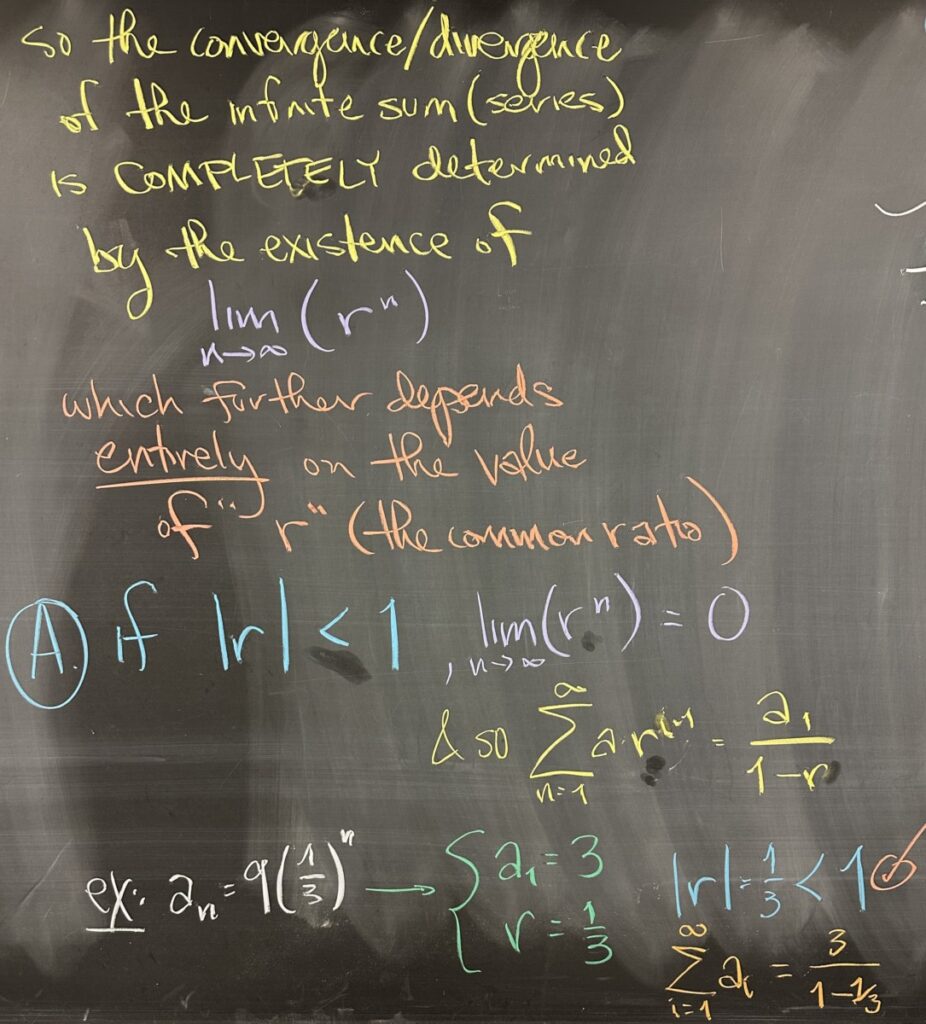
Since the only piece of \(\displaystyle\lim_{n\to\infty}(s_n)\) that contains an \(n\) is \(\displaystyle\lim_{n\to\infty}(r^n)\), the value of \(r\) is the only determining factor for the convergence of the series (the infinite sum).
So when does \(\displaystyle\lim_{n\to\infty}(r^n)\) exist?
\(r^n\) is an exponential function, and exponential functions have horizontal asymptotic behavior whenever \(|r|<1\), specifically \(\displaystyle\lim_{n\to\infty}(r^n)=0\)
With regards to the example from our first quiz problem, we have \(r=\frac13\), and as such, the series \(\displaystyle\sum_{i=1}^\infty 9(\frac13)^n\) converges to \(\displaystyle\frac{3}{1-\frac13}\).

Furthermore, we can conclude that if \(|r|\geq1\), the series \(\displaystyle\sum_{i=1}^\infty (ar^{n-1})\) will diverge.
Note that these conclusions are only valid for geometric series, because they have a very specific structure. In general, we will not have a closed form for \(s_n\), and as a result, we cannot compute \(\lim(s_n)\) as we did with geometric series.
In these general situations, the only closed form that we will have is for \(a_n\) (the original sequence, from which we build the series).

Since, in general, we won’t be able to compute the limit for series, we will instead use “series tests” to determine convergence or divergence (though we will often be unable to conclude what value these series converge to, if they happen to converge).
These series tests follow a consistent structure, a computation, a comparison, and then a conclusion.
We see this structure in the Geometric Series Test, which we just covered. First, we computed the absolute value of the common ratio, \(|r|\). Then, we compared \(|r|\) to \(1\). Finally, we conclude that the series converges if \(|r|<1\) or the series diverges if \(|r|\geq 1\).
We also have another series test to cover today: the Divergence Test. In short, the divergence test says that a series (infinite sum) has no chance of converging if the underlying sequence \(a_n\) converges to any number other than zero.
Be careful, however, because the Divergence Test has its name because it only proves divergence. In other words, even if \(\lim(a_n)=0\), we cannot conclude anything about \(\displaystyle\sum^\infty a_n\).
The structure for the Divergence Test is:
- compute: the limit of \(a_n\)
- compare: the limit to zero (equal or not equal)
- conclude: the series diverges (limit not equal to zero), or inconclusive (limit is equal to zero)




Recent Comments