Graphs of sine and cosine (Kate Poirier)
Estimating the height of a building (Suman Ganguli)
Borrowing and Saving (Kate Poirier)
Working Group
Graphs of sine and cosine (Kate Poirier)
Estimating the height of a building (Suman Ganguli)
Borrowing and Saving (Kate Poirier)
The following problems come from Arthur Kramer’s Fundamental of Technical Mathematics, second edition. With permission from Professor Kramer and from the Math Department Curriculum Committee, I will request these problems be adapted for the appropriate WeBWorK homework sets in MAT 1275. If anyone has comments, further requests, or suggestions, please let me know.
page 166 #44 (figure page 167)
Enrique is traveling parallel to a straight coastline in his motorboat and wants to find his distance from the shore Using a compass, he takes the bearing of the stack of a power plant and measures the angle between his heading and the stack to be 52 degrees. After he travels 0.30 mi, the angle between his heading and the stack is 90 degrees. How far is he from the coast?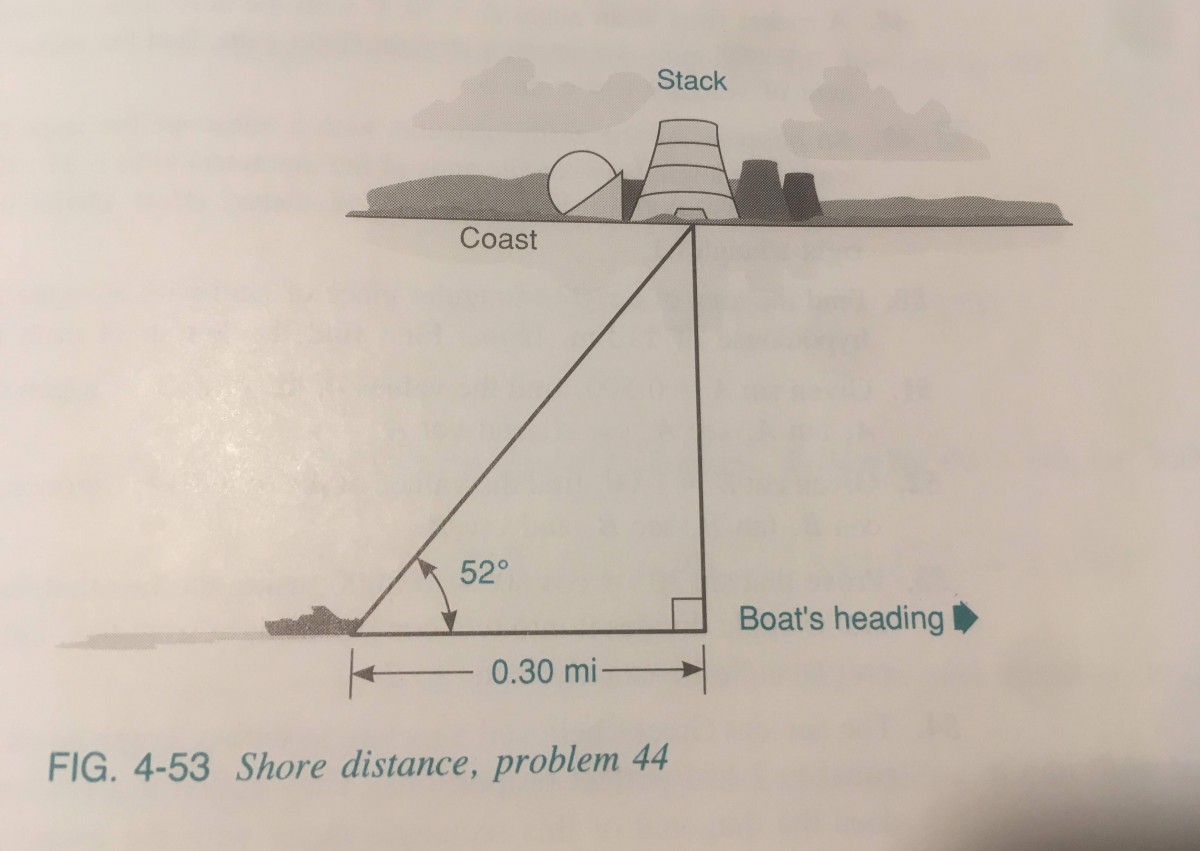
page 166 #43 (figure page 167)
The index of refraction of a medium is defined as the ratio of the speed of light c in air to the speed of light c_m in the medium. It is equal to:
where 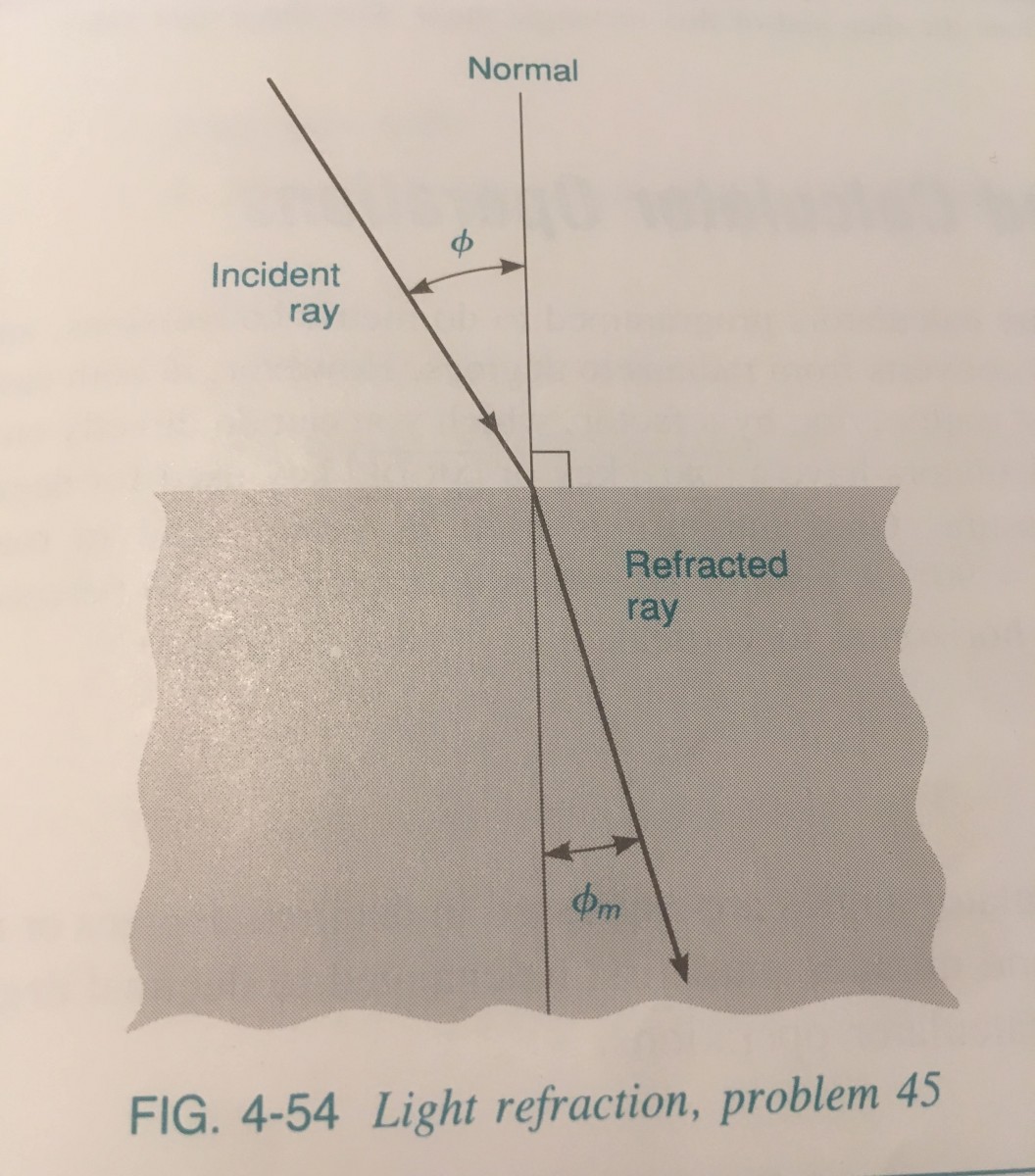
Adapted from Example 5-17 page 197 (figure page 197)
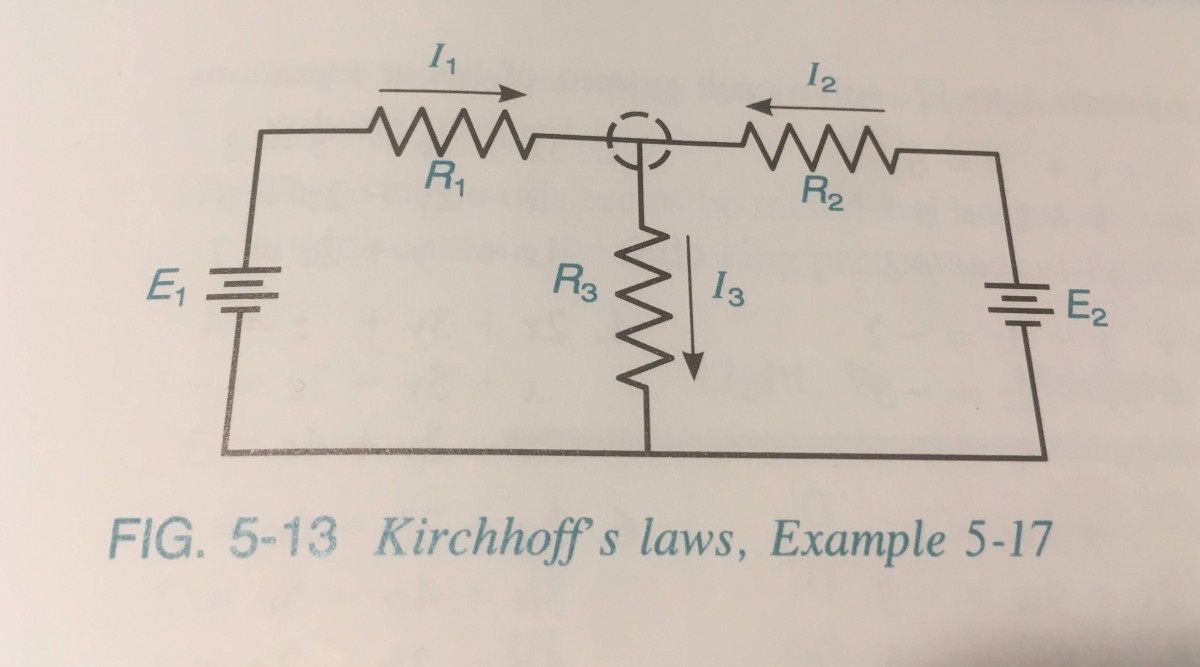 Kirchoff’s laws for the circuit in the figure yield the following three linear equations
Kirchoff’s laws for the circuit in the figure yield the following three linear equations
where
Let
The earth’s orbit around the sun and the moon’s orbit around the earth are approximate circles of radii
(a) on the positive
(b) in the first quadrant on the line
Page 284 #98
The velocity
Simplify and combine the terms, expressing
Masa has mentored many student projects. Several projects involve some kind of math and may provide ideas for math projects (in particular for Opening Gateways Faculty Fellows’ STEM Applications). Masa was generous enough to allow these projects to be posted here.
EESL_SmartCityObservatory_PatriceProsper (1)
Eco Composter Waste To Energy II City Tech (1)
IUSE Poster Presentation_MNreviewed (1)
Math liaisons, please encourage your students to register for a 3-day math preparatory workshop in August!
Click here for details.
Thursday, May 2; Faculty Commons conference room
3-4pm: MECH (Present: Masa Nakamura)
4-5pm: ETET (Present: Mohammed Kouar, Viviana Vladutescu)
Professor Johann Thiel is the course coordinator for MAT 2440 and 2540. His repository of projects that instructors can use in their classes is available here.
Thursday, April 18; Faculty Commons conference room
3-4pm: CET (Present: Aparicio Carranza, Yu Wang, Ohbong (John) Kwon
4-5:20pm: CST (Present: Candido Cabo, Bader Oudjehane, Ashwin Satyanarayana)
One of the goals of the STEM Liaison is to identify topics in science, technology, and engineering programs that could be introduced as applications of particular math topics in math courses. Through the Opening Gateways grant, faculty fellows have created STEM applications for MAT 1275 (College Algebra and Trigonometry) and MAT 1375 (Precalculus). Fellows will create STEM applications for MAT 1475 (Calculus I) in Fall 2019 and pilot these in their own classes in Spring 2020.
Here are links to STEM applications created by previous fellows:
© 2025 CityTech Math and STEM Liaisons
Theme by Anders Noren — Up ↑
Recent Comments