Welcome to the Math and STEM Liaison Working Group site. The site is a work in progress. Please take a look around!
Graphs of sine and cosine (Kate Poirier)
Estimating the height of a building (Suman Ganguli)
Borrowing and Saving (Kate Poirier)
- Arney, Guerra, Hughes, Novak, Patterson, Plucker, Wattenberg: From the Earth to the Moon and Mars and Back with Calculus and Physics
- Nasa has its own set of activities for different math classes: Exploring Space Through Math
- Ashwin Satyanarayana’s (Computer Systems Technology) ideas for MAT 1475 applications:
- Backpropagation algorithm for deep learning/machine learning/neural networks
- time complexity of algorithms
- gradient descent
- Masa Nakamura’s (Mechanical Engineering Technology) undergraduate students’ research projects
- Joel Greenstein’s Undergraduate Mathematics and its Application Project modules (if you are interested in a particular module that does not appear on this list, please request a scan/photocopy from Kate):
- Biology
- The digestive process of sheep
- Selection in genetics
- The human cough
- Population growth and the logistic curve
- Chemistry
- Kinetics of single reactant reactions
- Radioactive chains: parents and daughters
- Earth science and oceanography
- Listening to the earth: controlled source seismology
- Economics
- Feldman’s model
- The distribution of resources
- Differentiation, curve sketching, and cost functions
- Engineering
- Ascent descent
- Geography
- Mercator’s world map and the calculus
- Medicine
- Tracer methods in permeability
- Epidemics
- The human cough
- Measuring cardiac output
- Physics
- The human cough
- Ascent descent
- Physiology and psychology
- A strange result in visual perception
- American politics
- The dynamics of political mobilization
- A model of the mobilization process
- Deductive consequences and empirical applications of the model
- Exponential models of legislative turnover
- The dynamics of political mobilization
- Biology
- Johann Thiel’s MAT 2440/2540 (Discrete Structures and Algorithms I & II) project repository
The following problems come from Arthur Kramer’s Fundamental of Technical Mathematics, second edition. With permission from Professor Kramer and from the Math Department Curriculum Committee, I will request these problems be adapted for the appropriate WeBWorK homework sets in MAT 1275. If anyone has comments, further requests, or suggestions, please let me know.
-
page 166 #44 (figure page 167)
Enrique is traveling parallel to a straight coastline in his motorboat and wants to find his distance from the shore Using a compass, he takes the bearing of the stack of a power plant and measures the angle between his heading and the stack to be 52 degrees. After he travels 0.30 mi, the angle between his heading and the stack is 90 degrees. How far is he from the coast?
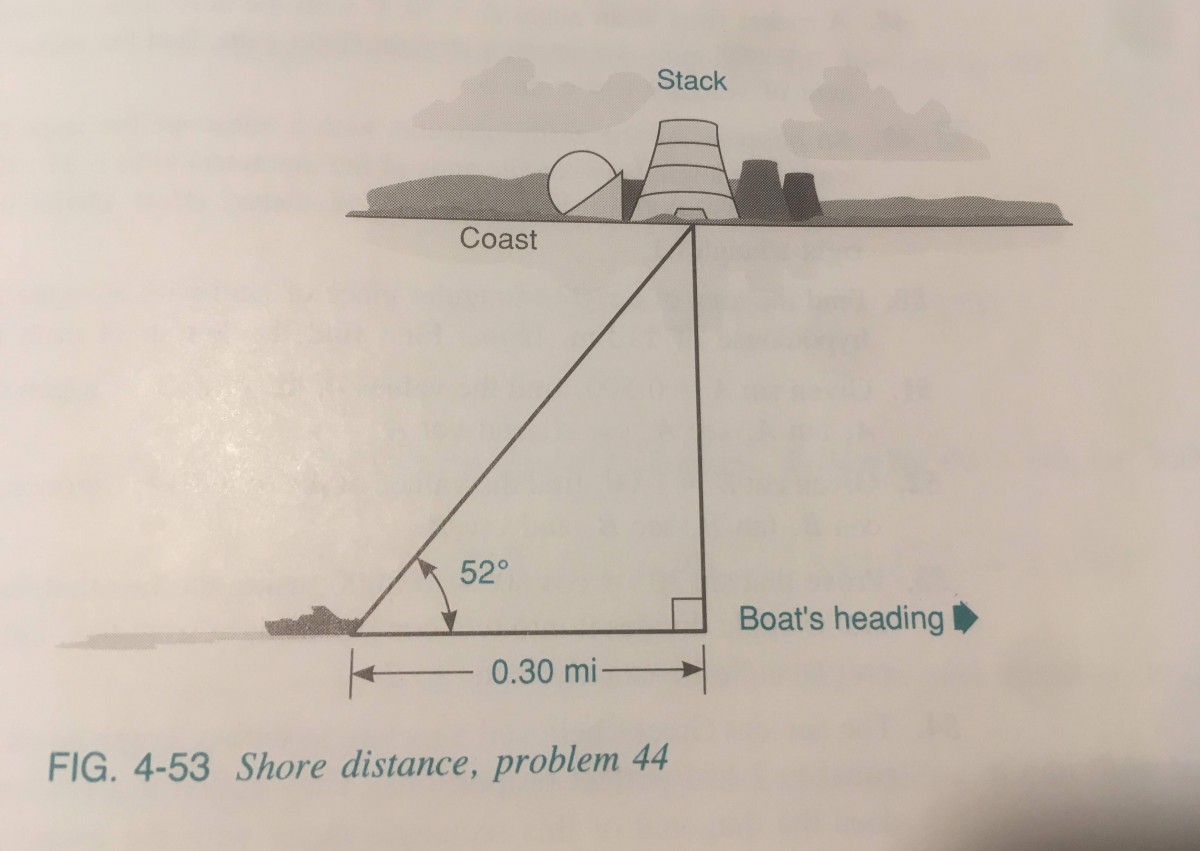
-
page 166 #43 (figure page 167)
The index of refraction of a medium is defined as the ratio of the speed of light c in air to the speed of light c_m in the medium. It is equal to:
\[\mu=\frac{c}{c_m} = \frac{\sin(\phi)}{\sin(\phi_m)}\]
where $\phi$ is the angle of incidence and $\phi_m$ is the angle of refraction of a light ray. If a ray of light passes from air into water, where $\mu = 1.33$ and $\phi = 0.254$ rad, find the angle of refraction $\phi_m$ in radians.
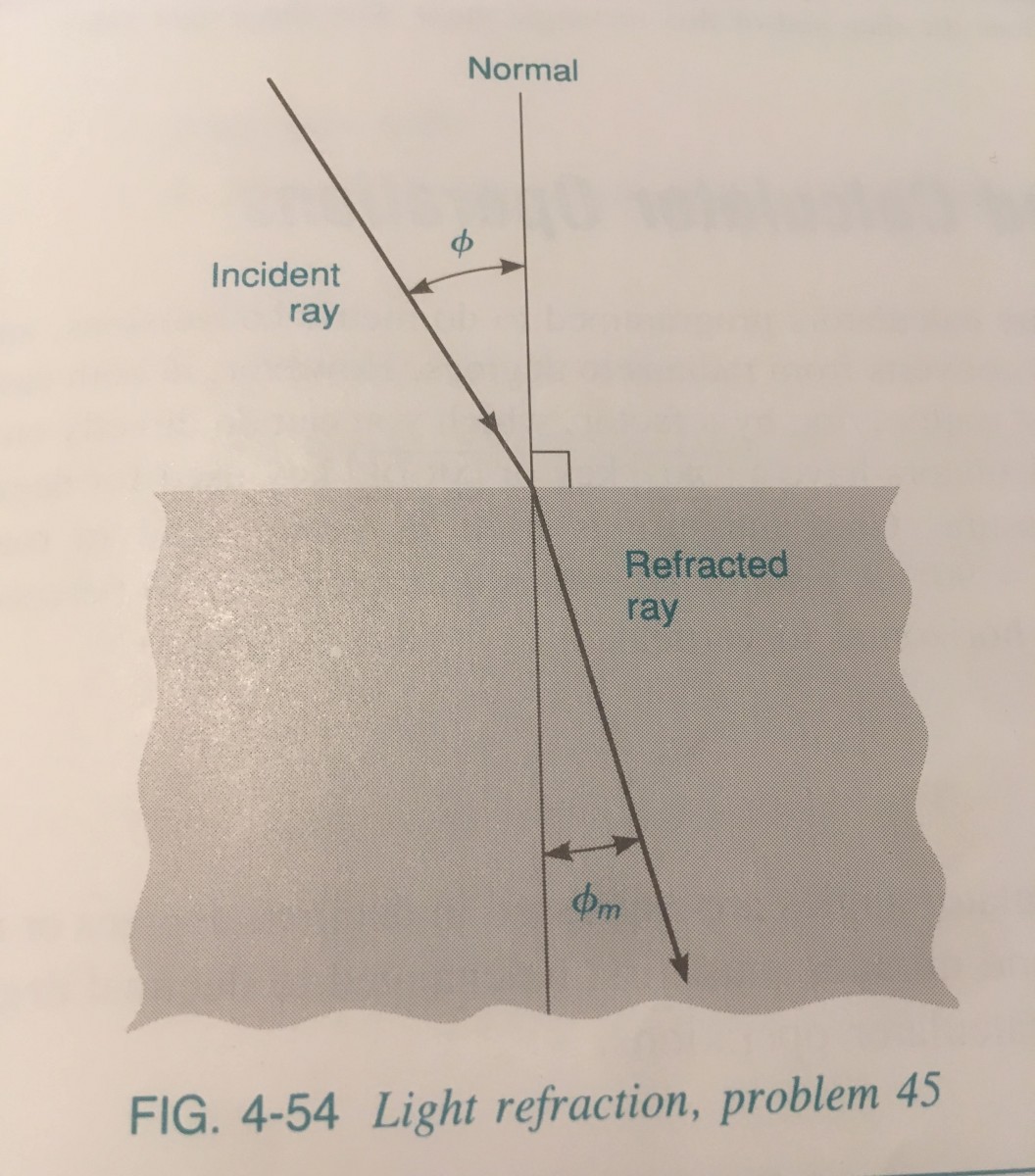
-
Adapted from Example 5-17 page 197 (figure page 197)
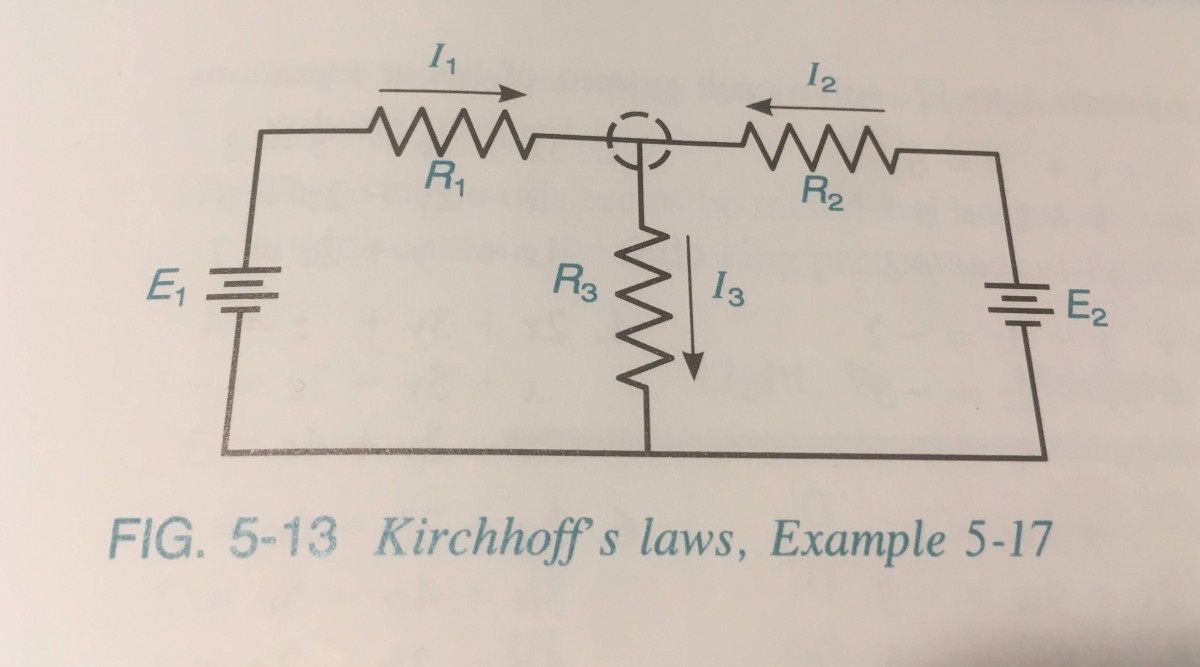 Kirchoff’s laws for the circuit in the figure yield the following three linear equations
Kirchoff’s laws for the circuit in the figure yield the following three linear equations\[ I_1 + I_2 -I_3 =0 \]
\[I_1 R_1 + I_3R_3 = E_1\]
\[I_2 R_2 + I_3R_3 = E_2\]
where $E_1$ and $E_2$ represent voltage, $R_1, R_2$, and $R_3$ represent resistances, and $I_1, I_2$, and $I_3$ represent current.
Let $E_1 = 14.0 V, E_2 = 12.6 V, R_1 = 6.00 \Omega, R_2 = 5.50 \Omega$, and $R_3 = 4.00 \Omega$. Find $I_1, I_2$, and $I_3$.
-
The earth’s orbit around the sun and the moon’s orbit around the earth are approximate circles of radii $1.5 \times 10^8$ and $3.8 \times 10^5$, respectively, where the sun is at the center of the earth’s orbit and the earth is at the center of the moon’s orbit. If the sun is placed at the origin of a coordinate system, what is the equation of moon’s orbit when the center of the earth is
(a) on the positive $x$ axis and
(b) in the first quadrant on the line $y=x$?
-
Page 284 #98
The velocity $V$ of a small water wave is given by:
\[ V = \sqrt{\frac{\pi}{4 \lambda d}} + \sqrt{\frac{4 \pi}{\lambda d}}.\]
Simplify and combine the terms, expressing $V$ with a rational denominator.
Masa has mentored many student projects. Several projects involve some kind of math and may provide ideas for math projects (in particular for Opening Gateways Faculty Fellows’ STEM Applications). Masa was generous enough to allow these projects to be posted here.
EESL_SmartCityObservatory_PatriceProsper (1)
Eco Composter Waste To Energy II City Tech (1)
IUSE Poster Presentation_MNreviewed (1)
Math liaisons, please encourage your students to register for a 3-day math preparatory workshop in August!
Click here for details.
Thursday, May 2; Faculty Commons conference room
3-4pm: MECH (Present: Masa Nakamura)
- The more advanced courses require math; some students take longer to complete the program depending on their initial placements in math courses. The goal for a Mechanical Engineering *Technology* program is not to let math requirements hold students back.
- Students with higher initial placement are advised to take linear algebra and statistics even though they are not program requirements (this way they can compete with students from mechanical engineering departments after graduation). Finite Element Methods (MECH 4730) actually requires linear algebra; while students are not required to take MAT 2580, they become familiar with matrices earlier in a course with MATLAB.
- Students’ placements have been improving in recent years; most used to place into MAT 1275 but now about a third of entering place into MAT 1475 (and thus have room for more math courses).
- Elementary concepts are still a huge challenge for students in courses with no math prerequisites (IND 1112 for example). This might be an issue in the future that could be addressed in MAT 1275CO if students who place into MAT 0650 are admitted to MAT 1275CO (it would help if the final exam included geometry topics). We discussed:
- plane geometry and parallel lines/angle results,
- a full rotation is 360 degrees,
- objects related by a reflection are not the equal.
- Unit conversion and calculations with units are widespread problems that could be addressed in any math course with appropriate examples and homework problems. Problems in Arthur Kramer’s (smaller) book on page 125 are suggestions.
- Three-dimensional visualization and drawing is extremely important. Students struggle to visualize simple 3D rotations. One idea might be to sneak 3D geometry (at least a picture of different types of solutions) into the section on 3×3 linear systems into MAT 1275/1275CO so that students see 3D Euclidean space at some point. This is already helpful pedagogically for any student, not just engineering students.
- Electrical engineering uses complex numbers but the notation for i is j! Arthur’s book may have a suitable problem.
- Masa’s research in environmental engineering sounds fascinating and does include some elementary math. He’s mentored students at all different levels and has found that environmental science/engineering is reasonably easy for non-experts to understand. This seems like a great place to look for project ideas.
- Mechanical engineering and civil engineering have a lot in common, so there is another place to look for applications.
4-5pm: ETET (Present: Mohammed Kouar, Viviana Vladutescu)
- Mohammed shared an old project he created with Nadia Benakli and Estela Rojas that looks perfect for integrating into MAT 1275 and 1375. It is a summary of basic math skills required for EET 1122.
- Circuit Analysis II (EET 1222) requires complex numbers and has MAT 1375 as a prerequisite…so students should have seen complex numbers at least once or twice before taking the course but seem not to remember. (Kate: This would be a good place to look for applications for examples/exercises.)
- We spent most of our time discussing Advanced Circuit Analysis (EET 2122).
- This course requires differentiation (starts about halfway through MAT 1475), integration (MAT 1575), and solving of differential equations (including by Laplace transform; at the end of MAT 2680). However, this course has only MAT 1475 (or higher) as a co-requisite.
- In Viviana’s class, the first five or six sessions are spent on a crash course in three semester’s worth of material.
- From a math perspective, this is a huge concern and not recommended at all. Students and instructors suffer from this aspect at the beginning of the course and from students weak foundation in these math topics throughout the course.
- Further, while Bachelor’s students are eventually required to take MAT 1575, they are not required to take MAT 2680 at all, even though a quick glance at the syllabus makes it seem like a number of topics (including circuit applications) are included in both courses.
- Viviana requested that at least the MAT 1475 co-requisite be changed to a prerequisite. Her own students who have already seen derivatives tend to do better in the course than those who have not. (Viviana will share scans of her notes.)
- Viviana and Mohammed discussed potential impacts of changing the prerequisites for the course and having students take it later in the program. It seems that since many students place into MAT 1275, practical concerns override curricular decisions.
- Relatedly, if a student follows the college catalog, they would take a math course every other semester, as opposed to in consecutive semesters, as is recommended. The sequencing in this part of the program appears in need of an overhaul.
- Update 5/17: I asked Viviana and Mohammed to encourage students taking EET 2122 in the fall to register for the appropriate math preparatory workshop in August.
Professor Johann Thiel is the course coordinator for MAT 2440 and 2540. His repository of projects that instructors can use in their classes is available here.
Thursday, April 18; Faculty Commons conference room
3-4pm: CET (Present: Aparicio Carranza, Yu Wang, Ohbong (John) Kwon
- Arthur Kramer’s books are great references for applications that can be inserted into many MAT courses
- the most important math content for CET students is statistics and linear algebra
- understanding physics applications can help students with understanding engineering applications
- topics mentioned: domains/ranges of functions (coming from real life), solving equations, scientific notation, units,(scientific) calculator
- project idea: use MATLAB (or programming language) and logical thinking to implement something using course material
- Fourier analysis is not on the MAT 2680 course outline but is important for CET 3625 students (these courses used to be coordinated but the coordination was lost with the recent MAT 2680 course outline change)
- The spring problems/RLC circuit sections of MAT 2680 are also important for these students; instructors should not skip these sections
- is it possible to create a course that combines elementary statistics with linear algebra?
4-5:20pm: CST (Present: Candido Cabo, Bader Oudjehane, Ashwin Satyanarayana)
- Ashwin’s ideas for MAT 1475 applications:
- Backpropagation algorithm for deep learning/machine learning/neural networks
- time complexity of algorithms
- gradient descent
- important topics for CST students:
- statistical analysis
- elementary probability
- important topics for data science students:
- linear algebra
- discrete models
- ideas for statistics/probability project:
- use a real-life example like a Photoshop image to motivate variance; write code to calculate variance
- similarly, applying a Photoshop filter is an example of a convolution
- MAT 2440/2540 examples and homework exercises look reasonable but students might not recognize that they’re encountering the same problem in different guises
- e.g., postage stamps (less relevant) versus data packets (more relevant)
- there are some elementary topics that many students struggle with that aren’t officially on MAT course outlines; could they be included somehow in homework problems so that students encounter them anyway? for example:
- percents
- unit conversion
- is it possible to tag a certain sections of MAT 2440/2540 for CST students and require programming for these sections only?
One of the goals of the STEM Liaison is to identify topics in science, technology, and engineering programs that could be introduced as applications of particular math topics in math courses. Through the Opening Gateways grant, faculty fellows have created STEM applications for MAT 1275 (College Algebra and Trigonometry) and MAT 1375 (Precalculus). Fellows will create STEM applications for MAT 1475 (Calculus I) in Fall 2019 and pilot these in their own classes in Spring 2020.
Here are links to STEM applications created by previous fellows:



Recent Comments