Category: Class Agendas (Page 1 of 9)

[Sorry for the delay in posting this class update]

Topics:

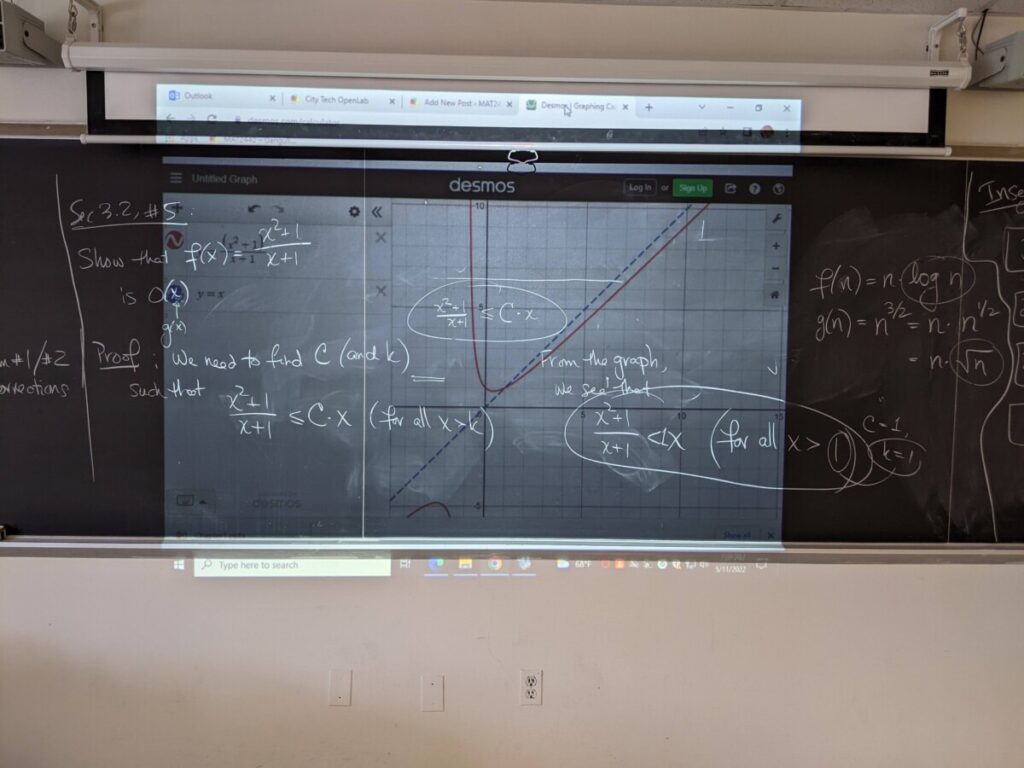
• reviewed HW#4 exercises from Sec 3.2 & 3.3:
  • Sec 3.2: shortcuts to figuring out big-O estimates for given functions (in particular polynomials, and functions that “look like” polynomials)
  • Sec 3.3: shortcuts to figuring out big-O estimates for given algorithms (in particular based on loops and nested loops)
• introduced Sec 5.1: Mathematical Induction
  • framework for a proof by induction: used to to prove a statement P(n) is true for all positive integers n, consists of two steps:
    • “base case” (usually P(1), i.e, show the statement holds for n = 1)
    • “induction step”: show that “P(k) implies P(k+1)” (for an arbitrary positive integer k)
  • sketched proof of “1 + 2 + 3 + … + n = n(n+1)/2”
    • see slides and/or Example 1 in Sec 5.1
• handed out Exam #3 (take-home due Thursday) – pdf also available via OpenLab Files

Schedule for remainder of semester:

• Wed May 18: finish mathematical induction; address Exam #3 questions; review for final exam
• Thurs May 19: Exam #3 due (either submit hard copy to math dept office (N711) or submit pdf via Blackboard)
• Fri May 20: Office hours (via Blackboard Collaborate) for final exam review and Exam #1/#2 corrections: 12-2p
• Mon May 23: Final exam, 12p-1:40p (& Exam #1/#2 corrections due)

Topics:

• Review insertion sort algorithm (Sec 3.1), look at its time complexity (Sec 3.3: O(n^2))
• HW#4 exercises from Sec 3.1 & 3.2:
  • Sec 3.1, #42 (insertion sort)
  • Sec 3.2, #5 & 23 (showing “big-O” relationships using graphs)

Schedule for remainder of semester:

• Thurs May 12 & Fri May 13: Office hours (via Blackboard Collaborate) for questions re HW#4
  • Thurs: 10a-11a
  • Fri: 12p-2p
• Mon May 16: HW#4 due; hand out Exam #3 (take-home)
• Wed May 18: Exam #3 due
• Thurs May 19 & Fri May 20: Office hours (via Blackboard Collaborate) for final exam review (times TBA)
• Mon May 23: Final exam

Boardshots:

Agenda/topics:

• Finish Sec 3.2 / 3.3:
  • review mathematical definitions (and intuitive understanding) of
    • “big-O” notation (upper bound)
    • “big-Ω” (big-Omega) notation (lower bound)
    • “big-Θ” (big-Theta) notation (both upper and lower bound)
    • “Big-O gives an upper bound on the growth of a function, while Big-Omega gives a lower bound. Big-Omega tells us that a function grows at least as fast as another.”
  • look at relevant video lectures/slides from Coursera Algorithms course
  • HW#4 exercises from Sec 3.2 & Sec 3.3

To Do:

• hand in Quiz #3: take-home quiz re linear search
• continue working on HW#4! due next Monday (May 16)

Boardshots:

TBA