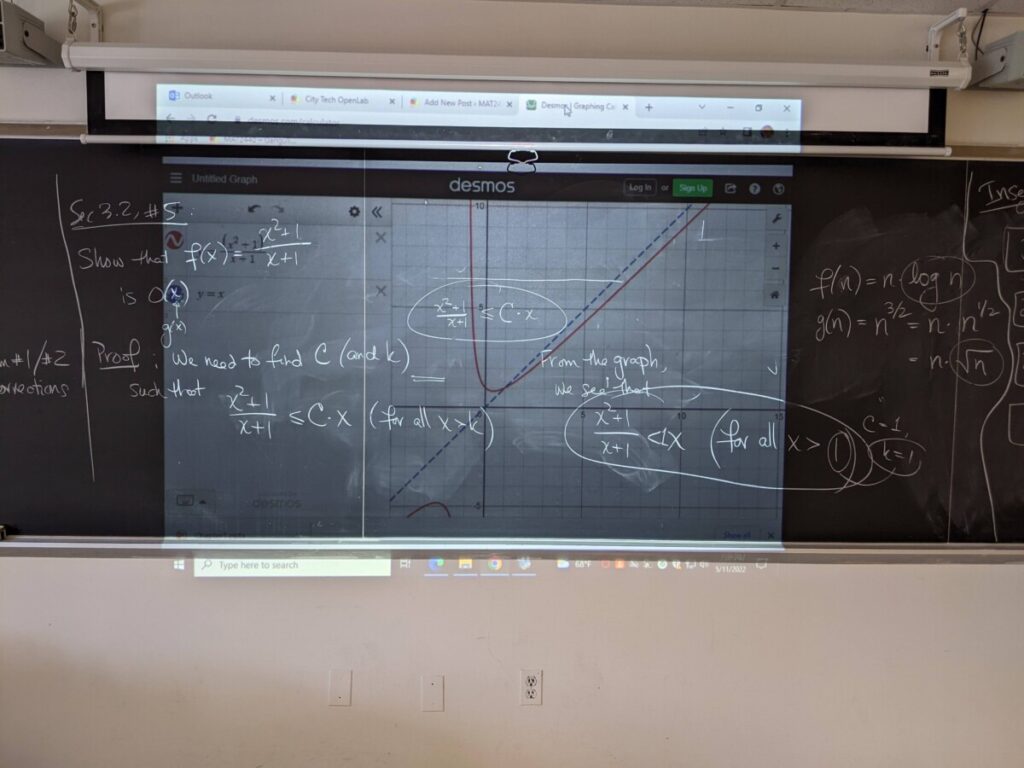
Coursera is a massive open online course (“MOOC”) platform created by Stanford CS professors a decade ago. I just noticed they are offering a free Princeton University algorithms course: https://www.coursera.org/learn/algorithms-part1
Here is the course description:
This course covers the essential information that every serious programmer needs to know about algorithms and data structures, with emphasis on applications and scientific performance analysis of Java implementations. Part I covers elementary data structures, sorting, and searching algorithms. Part II focuses on graph- and string-processing algorithms.
There is some overlap with what we are covering in Chapter 3, but it looks like this course will go much further in depth. It looks like it may also overlap somewhat with CST3650 (Data Structures).
If you are serious about continuing with computer science/programming, I would strongly suggest working through this course–perhaps this summer, if you have time.
Here are parts of the Coursera course which overlap with our course:
For example, here is a very nice and relevant screenshot from the “Order-of-Growth Classifications” lecture:

You could also look at the Week 3 lectures, which cover two more advanced sorting algorithms:
Here is a screenshot from the lecture on mergesort, which is an example of a “recursive” algorithm (the topic of recursion and recursive algorithms is covered in MAT2540 and Sections 5.3 & 5.4 of the Rosen textbook; see also the wikipedia entry for Recursion):






Recent Comments