Just a reminder that we will have our final exam on Monday, during our regular class time.
A handful of people logged on to Blackboard Collaborate for office hours earlier today. I recorded the session, so you can view the recording on Blackboard (go to our Collaborate Ultra page and click on the menu button in the upper left to switch to “Recordings”)
I went over a mathematical induction proof, reviewed some basic algorithms in pseudocode, and outlined what sort of topics/exercises to review for the final:
- propositional logic e.g., truth table: see Exam #1
- direct proofs and indirect proofs (i.e., proofs by contraposition): see Quiz #2 and Exam #2
- set operations and functions (including domain/range, definitions of one-to-one and onto functions): see Exam #2
- algorithms (writing simple algorithms in pseudocode; executing the basic search and sorting algorithms; big-O estimates of running-times): Exam #3 & Quiz #3
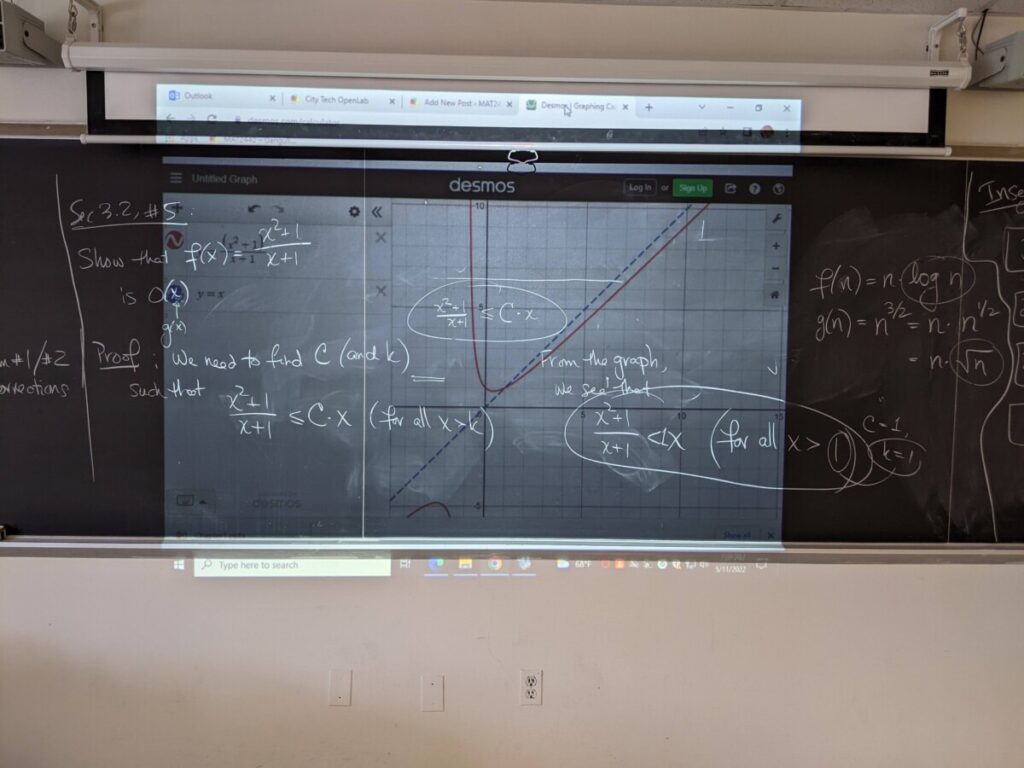
- proof by mathematical induction: Exam #3 & Sec 5.1
I will post solutions to Exam #3 and Quiz #3, so that you can review the solutions of those.





Recent Comments