Class Info
- Date: Wed Nov 29
- Meeting Info: 10a-11:40a, N719
Announcements
WebWork:
- “Series – Infinite Series” – due Mon Dec 4
- “Series – Divergence Test” – due Wed Dec 6
- additional WebWorks on infinite series will be assigned as we cover the topics in class, so please keep up with the WebWork!
Topics
We summarized geometric series, and went through a couple more examples from “Series – Infinite Series” that involve a “sum rule” for infinite series:


We then introduced the Divergence Test (or “n-th term test”)–if the individual terms in the series do not go to zero, then clearly the series diverges! This is covered in Sec 5.3.
We applied it to examples of infinite series where the n-th term is a ratio of two polynomials of equal degree:
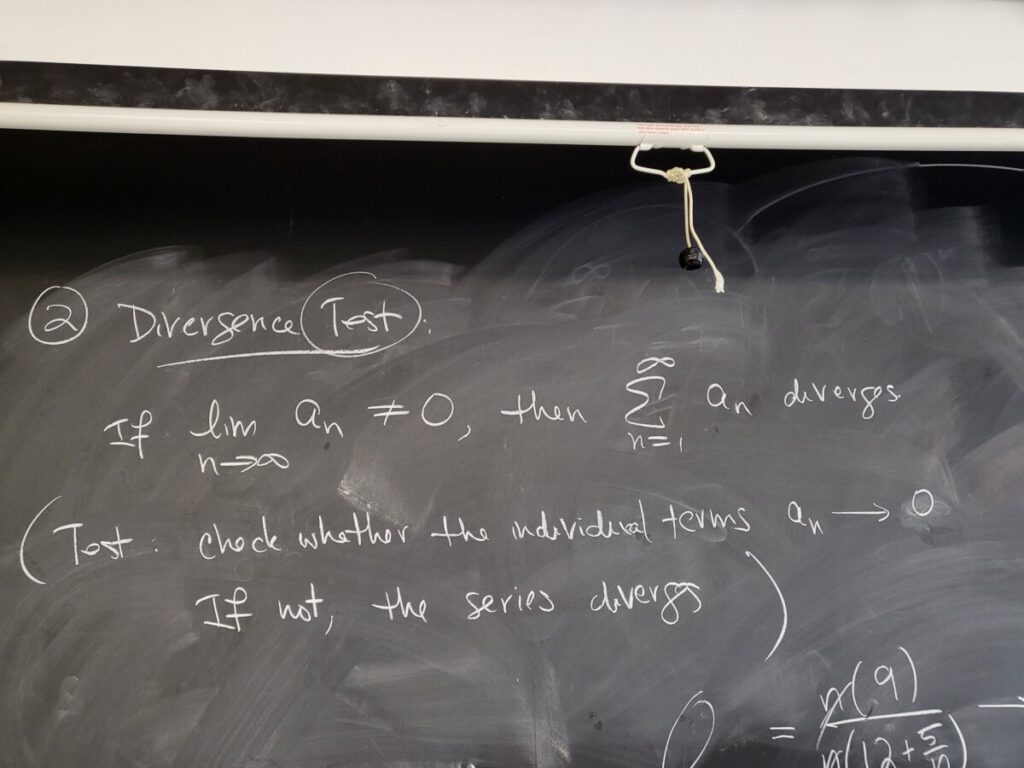


Finally, we discussed the harmonic series–this is the classic example of an infinite series where the individual terms do go to zero, but the series diverges!
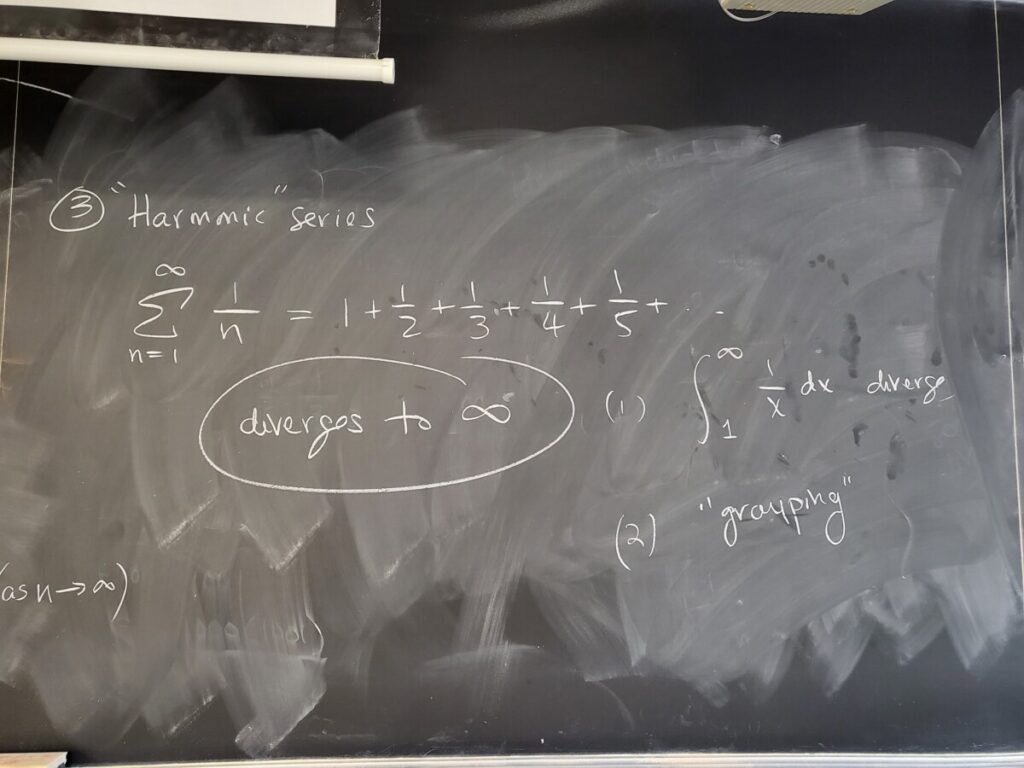
We sketched one proof of divergence last week, with the integral test (which is covered in Sec 5.3, after the Divergence Test).
Another proof of divergence is by “grouping” terms in the series together, as shown in the textbook (Sec 5.2):

We looked briefly at the wikipedia page for the harmonic series, which includes the two different proofs of its divergence.
Print this page



Leave a Reply