Month: October 2023 (Page 1 of 3)

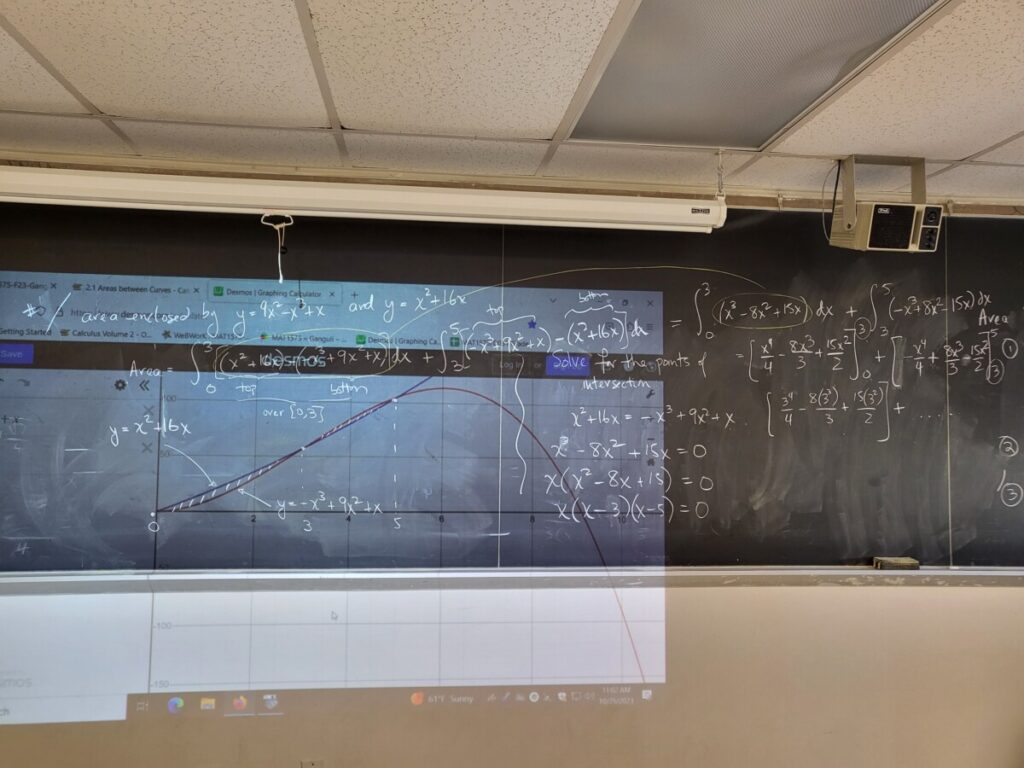
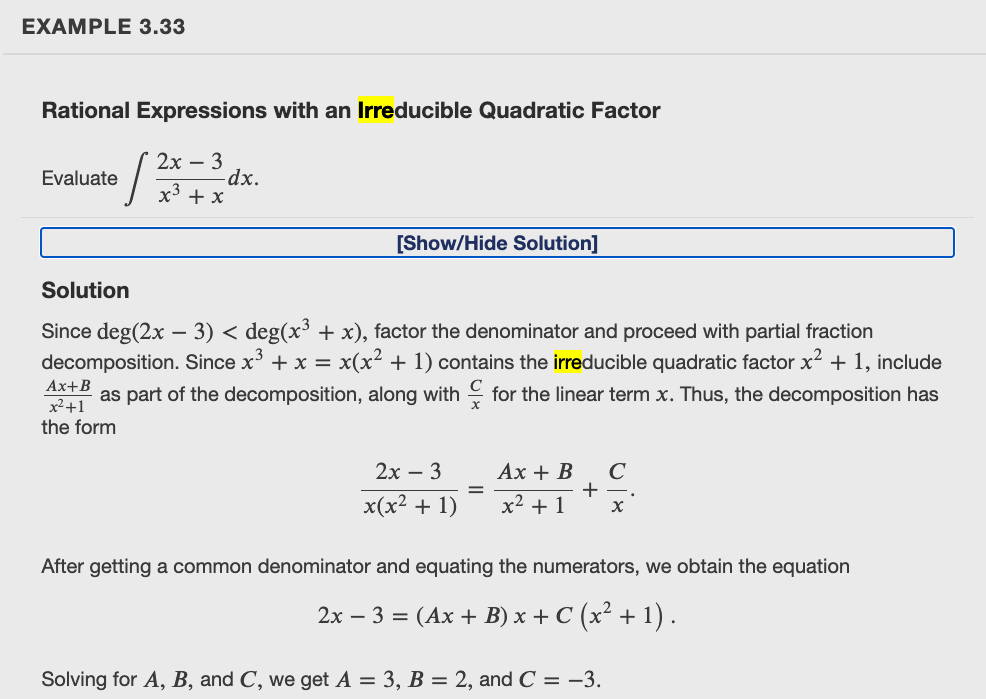
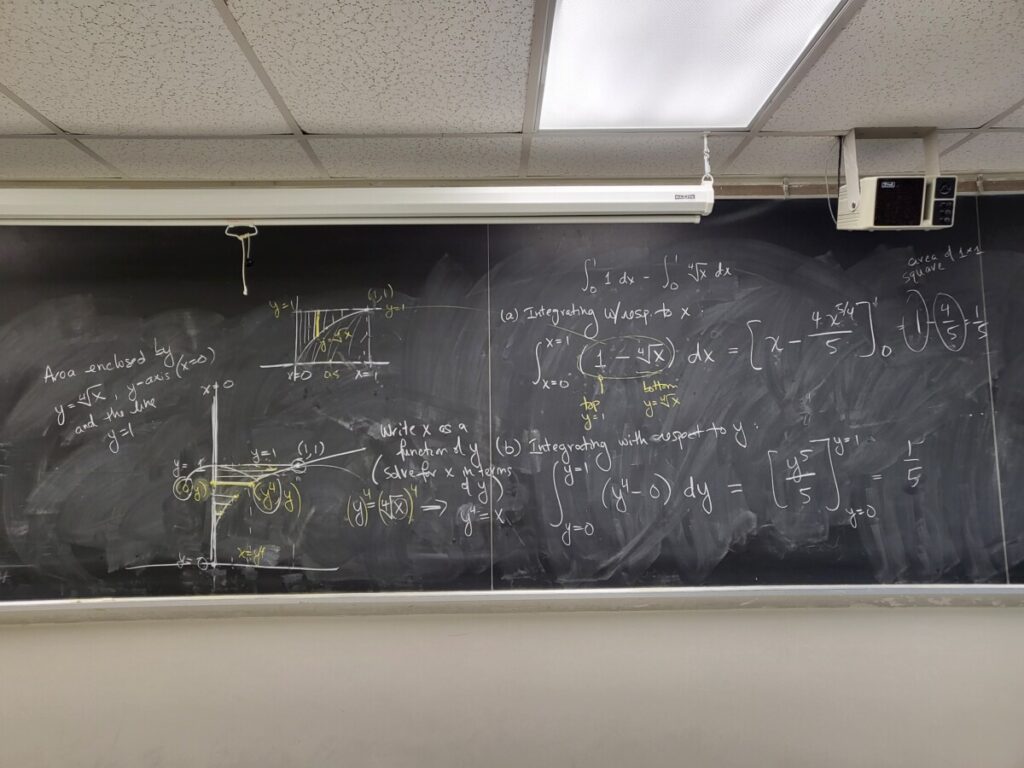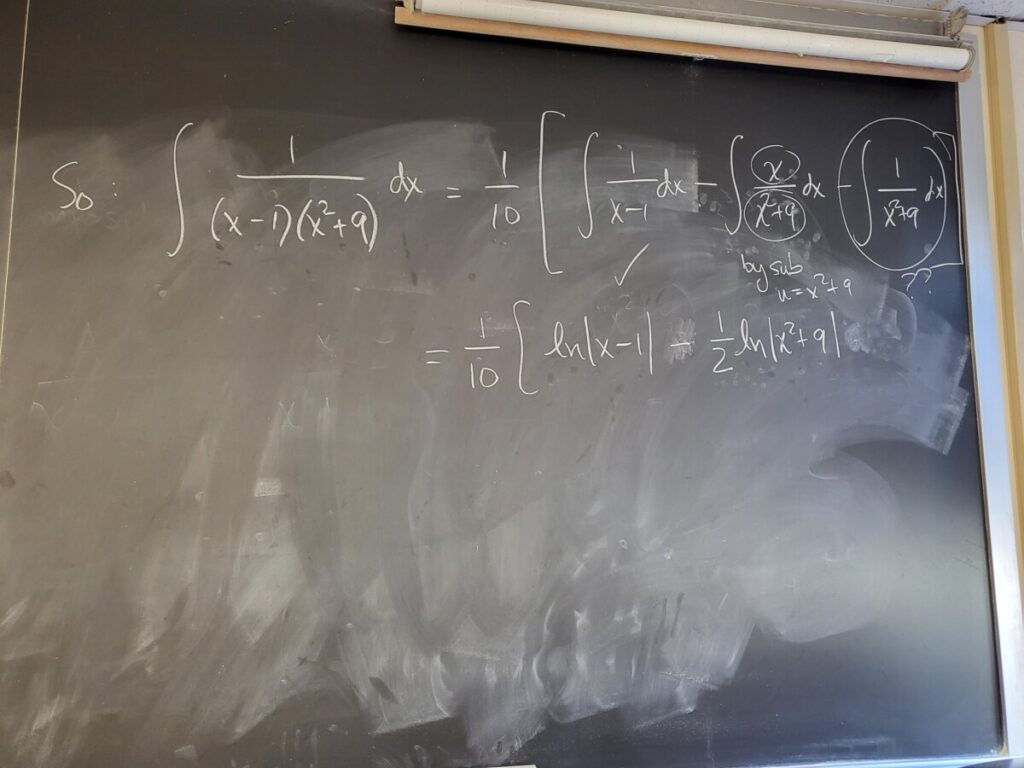Class Info

• Date: Mon Oct 30
• Meeting Info: 10a-11:40a, N719

Announcements

WebWork:

• finish “Integration – Partial Fractions” (due tonight – Mon Oct 30)
• “Applications – Areas Between Curves” (due Fri Nov 3)
• “Applications – Volumes of Revolution” (due Nov 8)

Topics

We went through some examples of computing “volumes by slicing” (covered in Sec 2.2 of the textbook) which also called “the disk method”–since we form the definite integral for the volume by picturing the object “sliced” into thin disks.

We first calculated the volume of a cylinder and the volume of a cone using this method. In the first case, the “cross-sectional” area is a constant; for a cone, the cross-sectional area is a circle whose radius is a linear function of x:

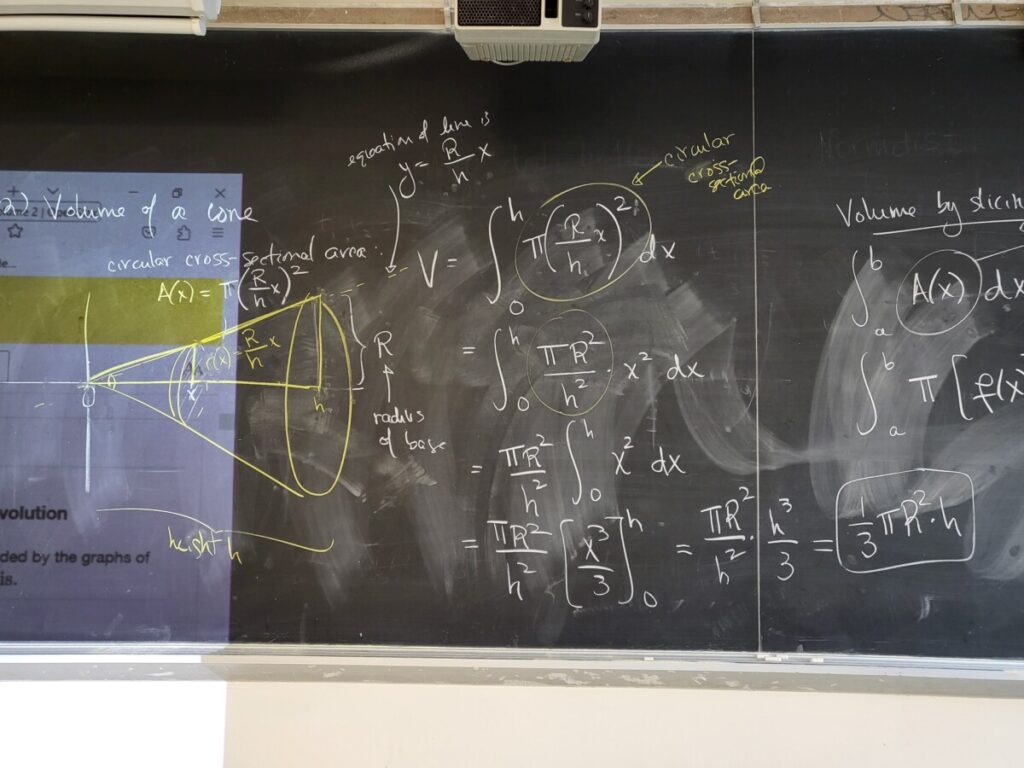
This leads to the general form of the definite integral for calculating a volume by slicing, in terms of the cross-sectional area; and the particular form of that for a “solid of revolution”:

We set up Example 2.7 from Sec 2.2 of the textbook:

We then went through the first few exercises from the “Applications – Volumes of Revolution” WebWork set. Here is #3:

Here is a video that illustrates the disk method, and a variation called “the washer method”:

Some of the subsequent exercises in that WebWork set use a different technique for computing volumes, called “cylindrical shells.” We will discuss that topic on Wednesday.

Class Info

• Date: Wed Oct 25
• Meeting Info: 10a-11:40a, N719

Announcements

WebWork:

• finish “Integration – Partial Fractions” (extended to Mon Oct 30)
• work on “Applications – Areas Between Curves” (due Wed Nov 1)

Topics

We went through some examples of computing “areas between curves” from the WebWork. This the first of some applications of integration we will study:

Here is the example we set up in class Monday:

As illustrated above, the general strategy involves identifying which curve (i.e., function) is “the top boundary” of the area and which is the “bottom boundary.” And in many examples (such as the one above) we have to solve for where the curves intersect, in order to figure out the endpoints of the interval of integration:

Here is a more complicated example we set up in class (Problem 3 on the WebWork). The two curves intersect at 3 points, with which curve is on top switching at the middle point. So we need to set up two separate integrals for the total area enclosed:

We also discussed an example (Problem 5) where it is more convenient to integrate with respect to y:

Here is the video I posted in the previous Class Recap:

And here is a followup video showing an example of integrating with respect to y:

Class Info

• Date: Mon Oct 23
• Meeting Info: 10a-11:40a, N719

Announcements

WebWork:

• finish “Integration – Integration by Parts” (extended to Mon Oct 30)
• work on “Area Between Curves”

Topics

We went through one more examples from the WebWork “Integration – Partial Fractions”–a longer more challenging exercise, given that it involves “an irreducible quadratic factor” in the denominator (i.e., a quadratic that can’t be factored further–in this case “x^2 + 9”:

For such a factor, we have to use a linear factor numerator (“Bx+C”) above, and we have to use the “method of equating coefficients” to solve for B and C (since there’s no x-values which make the irreducible quadratic factor 0!):

The last steps, in order to integrate is to split up the numerator over the quadratic factor into two separate terms:

We can solve the first two integrals. But for the last integral–the constant over x^2+9–we need the following “inverse trig” integral:

We mentioned that you can also study Example 3.33 Sec 3.4 of the textbook, which involves the (simpler) irreducible quadratic factor x^2+1:

We finished the class by starting to look at how to set up definite integrals to calculate “areas between curves”:

Here is a video with some similar examples: