Lesson 19: Inverse trigonometric functions

Hi everyone! Read through the material below, watch the videos.

Topic: This lesson covers Chapter 19: Inverse trigonometric functions.

WeBWorK: There is one WeBWorK assignment on today’s material:

Trigonometry – Inverse Functions

Question of the Day: Are the trigonometric functions $\sin(x),\cos(x)$ and $\tan(x)$ one-to-one functions?

The functions $\sin^{-1}, \cos^{-1},\tan^{-1}$

In this section, we are interested in the inverse functions of the trigonometric functions $y=\sin(x), y=\cos(x),$ and $y=\tan(x)$. You may recall from our work earlier in the semester that in order for a function to have an inverse, it must be one-to-one (or pass the horizontal line test: any horizontal line intersects the graph at most once).

The function $\tan^{-1}(x)$

Recall the graph of the function $y=\tan(x)$:

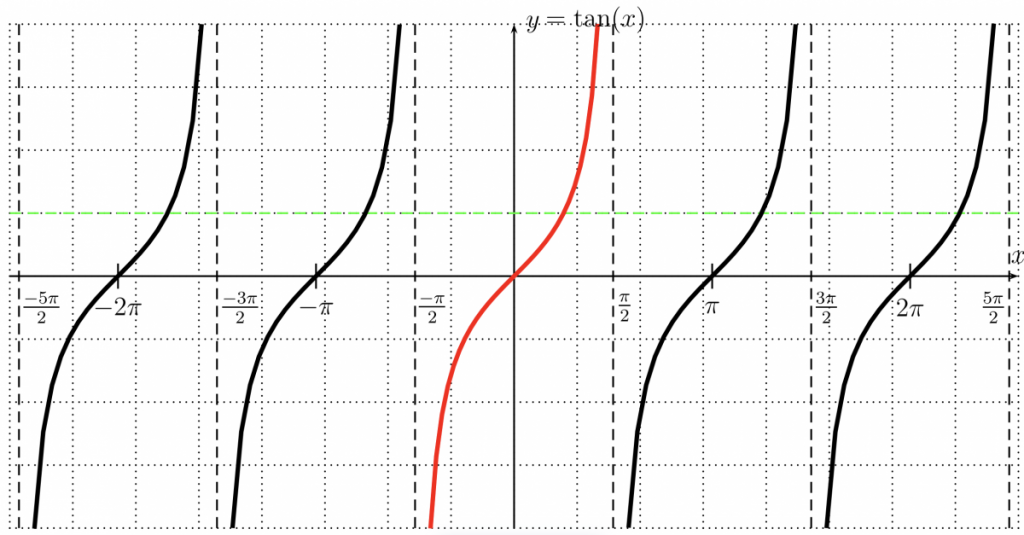
Notice that since the graph consists of a repeating pattern of vertical stripes, any horizontal line will touch the graph in multiple places – this graph FAILS the horizontal line test (it is NOT one-to-one). How can we define the inverse? By restricting the domain – that is, only looking at one of the repeating vertical stripes. If we only look at the part of the graph between $-\frac{\pi}{2}$ and $\frac{\pi}{2}$ then the function is one-to-one (that it, the red part of the function above is, by itself, one-to-one).

Definition 19.1. The inverse of the function $y=\tan (x)$ with restricted domain $D=\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$ and range $R=\mathbb{R}$ is called the inverse tangent or arctangent function. It is denoted by:
$y=\tan ^{-1}(x) \quad$ or $\quad y=\arctan (x) \quad \Longleftrightarrow \quad \tan (y)=x, \quad y \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$

Note that the inverse tangent function is written both $\tan^{-1}(x)$ and $\arctan(x)$ — they mean the same thing.

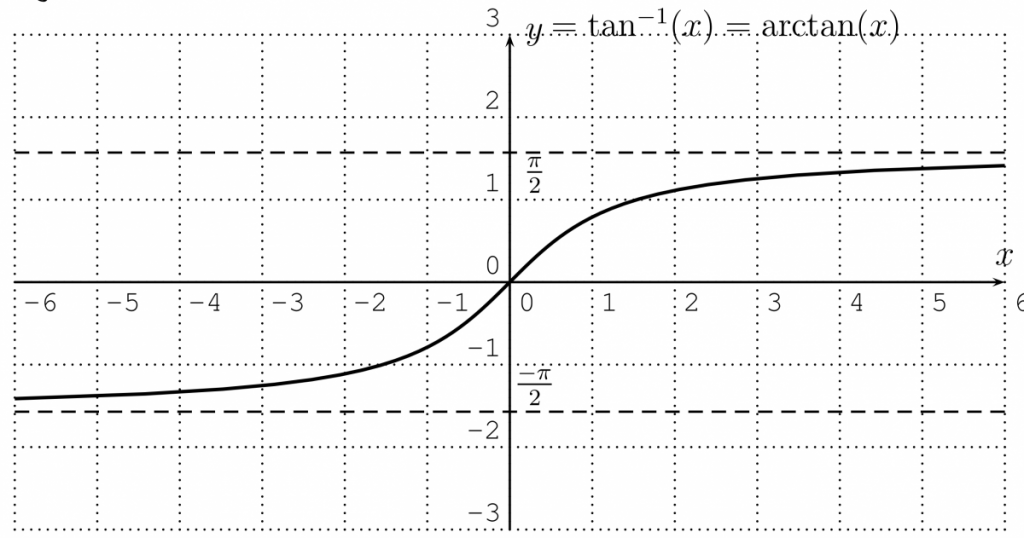
Observation: The inverse tangent is an odd function, so $\tan^{-1}(-x)=-\tan^{-1}(x)$
(recall that a function $f(x)$ is odd provided $f(-x)=-f(x)$)

Example 19.1 Recall the exact values of the tangent function from Chapter 17:

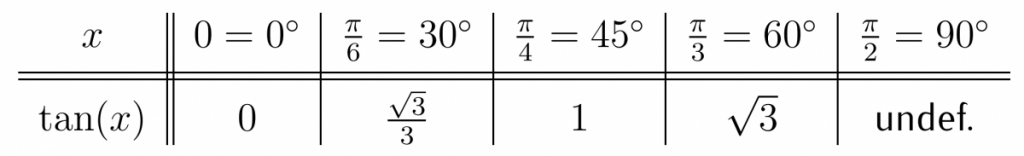
Use the table and Observation above to find exact values of the inverse tangent function. Give answers in both degrees and radians.
a. $\arctan(1)$ b. $\arctan\left(-\frac{\sqrt{3}}{3}\right)$. c. $\tan^{-1}(0)$

THE FUNCTION $\sin^{-1}(x)$

Consider the graph of the function $y=\sin(x)$. It is not one-to-one either:

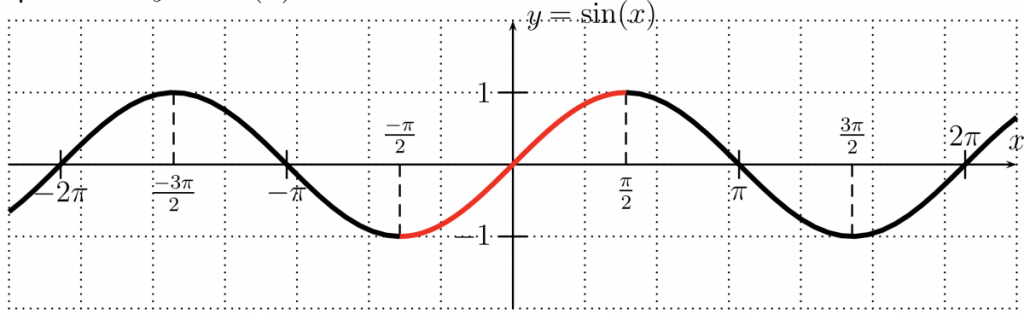
However, if we restrict the function to the interval $\left[-\frac{\pi}{2},\frac{\pi}{2}\right]$ (shown in red) the resulting function is one-to-one, and so we can consider the inverse function.

Definition 19.5. The inverse of the function $y=\sin (x)$ with restricted domain $D=\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$ and range $R=[-1,1]$ is called the inverse sine or arcsine function. It is denoted by
$y=\sin ^{-1}(x) \quad \text { or } \quad y=\arcsin (x) \quad \Longleftrightarrow \quad \sin (y)=x, \quad y \in\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$
The arcsine reverses the input and output of the sine function, so that the arcsine has domain $D=[-1,1]$ and range $R=\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$.

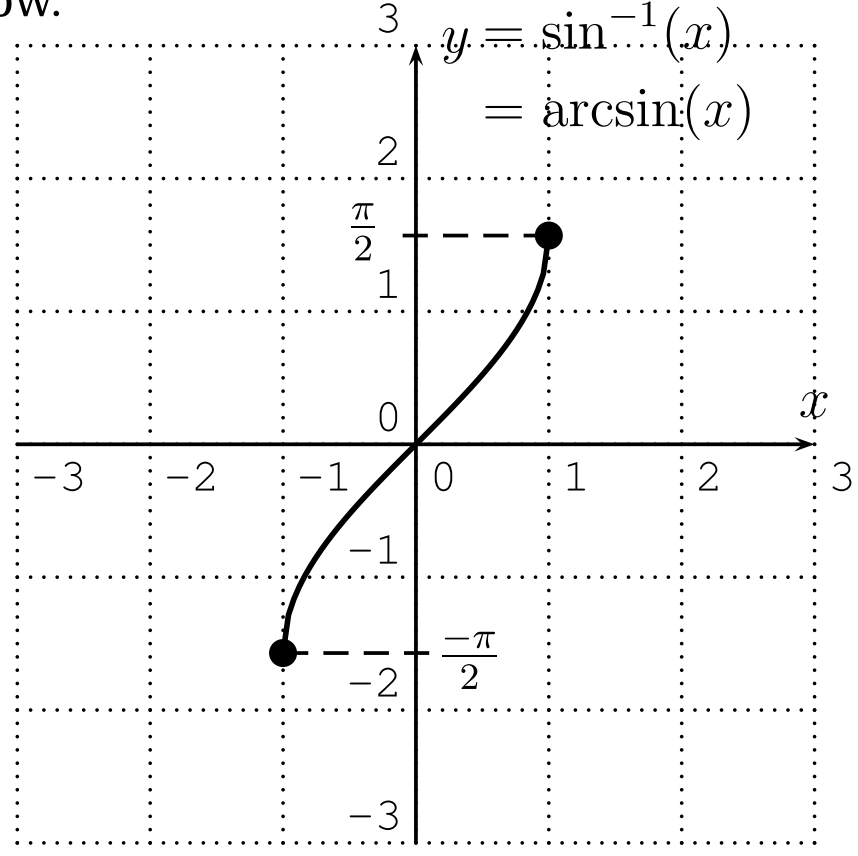
Observation: The inverse sine function is an odd function, so $\sin^{-1}(-x)=-\sin^{-1}(x)$.

Example 19.7. Recall the values of the sine function for common angles:

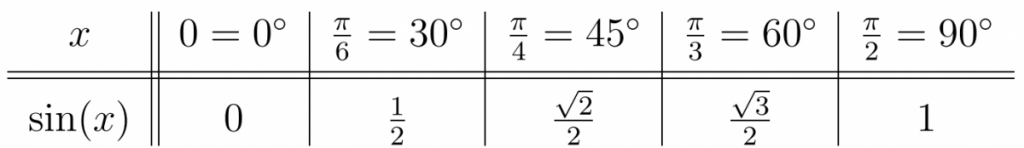
Use the Table and Observation above to find exact values of the arcsine function. Give answers in both degrees and radians.
a. $\sin ^{-1}\left(\frac{\sqrt{2}}{2}\right)$, b. $\sin^{-1}(1)$, c. $\sin^{-1}(0)$, d. $\sin ^{-1}\left(\frac{-1}{2}\right)$, e. $\sin^{-1}(3)$

THE FUNCTION $\cos^{-1}(x)$

We treat the function $\cos(x)$ similar to $\sin(x)$. However, we are no longer able to use the interval $\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$. Why?

In order to make the cosine function one-to-one, we restrict to the interval $[0,\pi]$.

Definition 19.8. The inverse of the function $y=\cos (x)$ with restricted domain $D=[0, \pi]$ and range $R=[-1,1]$ is called the inverse cosine or arccosine function. It is denoted by
$y=\cos ^{-1}(x) \quad \text { or } \quad y=\arccos (x) \quad \Longleftrightarrow \quad \cos (y)=x, \quad y \in[0, \pi]$
The arccosine reverses the input and output of the cosine function, so that the arccosine has domain $D=[-1,1]$ and range $R=[0, \pi]$.

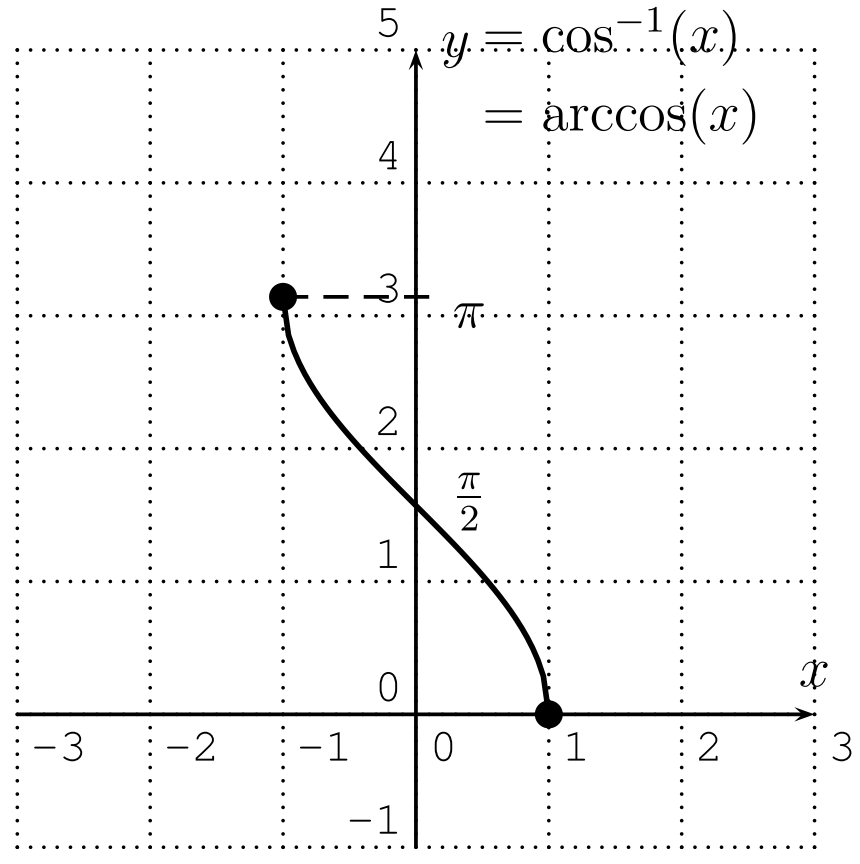
Observation: The arccosine function is neither even nor odd. However, it does obey the following symmetry: $\cos^{-1}(-x)=\pi-\cos^{-1}(x)$
(in many problems, you can avoid the use of this formula by remembering the unit circle definition of cosine).

Example 19.10. Recall the values of the cosine function for common angles:

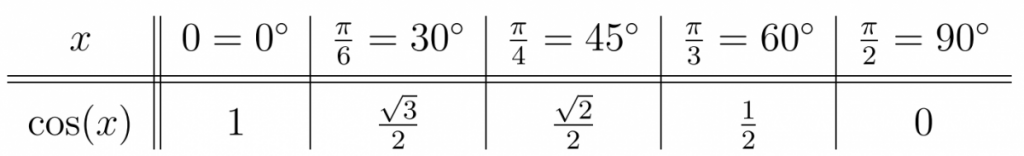
Use the Table and Observation above to find exact values of the arccosine function. Give answers in both degrees and radians.
a. $\arccos\left(\frac{\sqrt{3}}{2}\right)$, b. $\cos^{-1}(1)$, c. $\cos ^{-1}(0)$, d. $\arccos=\left(-\frac{1}{2}\right)$, e. $\arccos(2)$

Inverse trig functions on the TI-84+ calculator

How do we find values of inverse trig functions that don’t appear in our “common angles” table?

Example. Find the values of the inverse trig functions using a calculator. Include at least 5 decimal digits past the decimal point.

a. $\arccos(0.35)$ (in radians)
b. $\tan^{-1}(-13.2)$ (in degrees)

Print this page