Hi everyone! Read through the material below, watch the videos, and send me your questions. Don’t forget to complete the Daily Quiz (below this post) before midnight to be marked present for the day.
Lesson 19: Inverse trigonometric functions
Lesson Date: Tuesday, April 21st.
Topic: This lesson covers Chapter 19: Inverse trigonometric functions.
WeBWorK: There is one WeBWorK assignment on today’s material, due next Tuesday 4/28:
Trigonometry – Inverse Functions
Question of the Day: Are the trigonometric functions $\sin(x),\cos(x)$ and $\tan(x)$ one-to-one functions?
Lesson NOtes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
The functions $\sin^{-1}, \cos^{-1},\tan^{-1}$
In this section, we are interested in the inverse functions of the trigonometric functions $y=\sin(x), y=\cos(x),$ and $y=\tan(x)$. You may recall from our work earlier in the semester that in order for a function to have an inverse, it must be one-to-one (or pass the horizontal line test: any horizontal line intersects the graph at most once).
The function $\tan^{-1}(x)$
Recall the graph of the function $y=\tan(x)$:
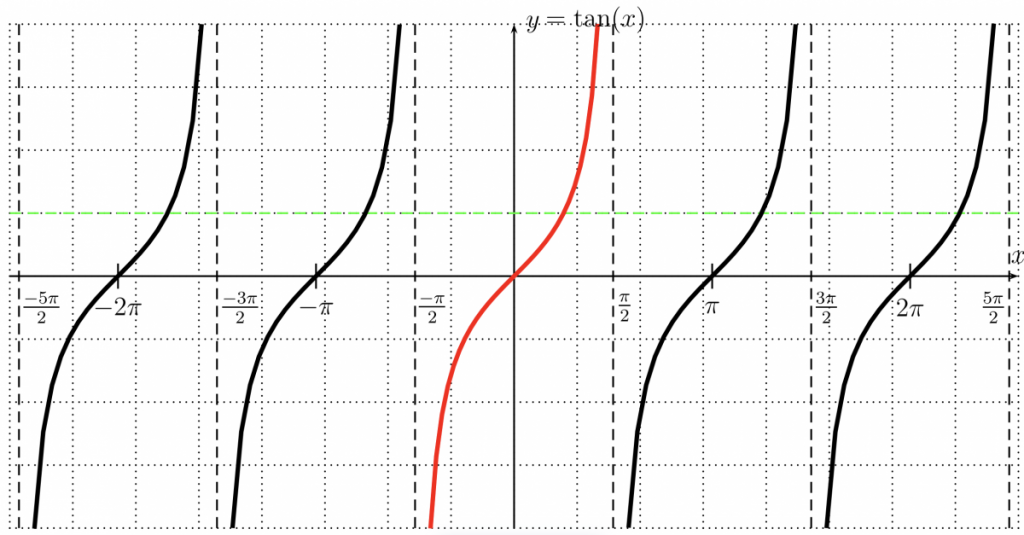
Notice that since the graph consists of a repeating pattern of vertical stripes, any horizontal line will touch the graph in multiple places – this graph FAILS the horizontal line test (it is NOT one-to-one). How can we define the inverse? By restricting the domain – that is, only looking at one of the repeating vertical stripes. If we only look at the part of the graph between $-\frac{\pi}{2}$ and $\frac{\pi}{2}$ then the function is one-to-one (that it, the red part of the function above is, by itself, one-to-one).
Definition 19.1. The inverse of the function $y=\tan (x)$ with restricted domain $D=\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$ and range $R=\mathbb{R}$ is called the inverse tangent or arctangent function. It is denoted by:
$y=\tan ^{-1}(x) \quad$ or $\quad y=\arctan (x) \quad \Longleftrightarrow \quad \tan (y)=x, \quad y \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$
Note that the inverse tangent function is written both $\tan^{-1}(x)$ and $\arctan(x)$ — they mean the same thing.
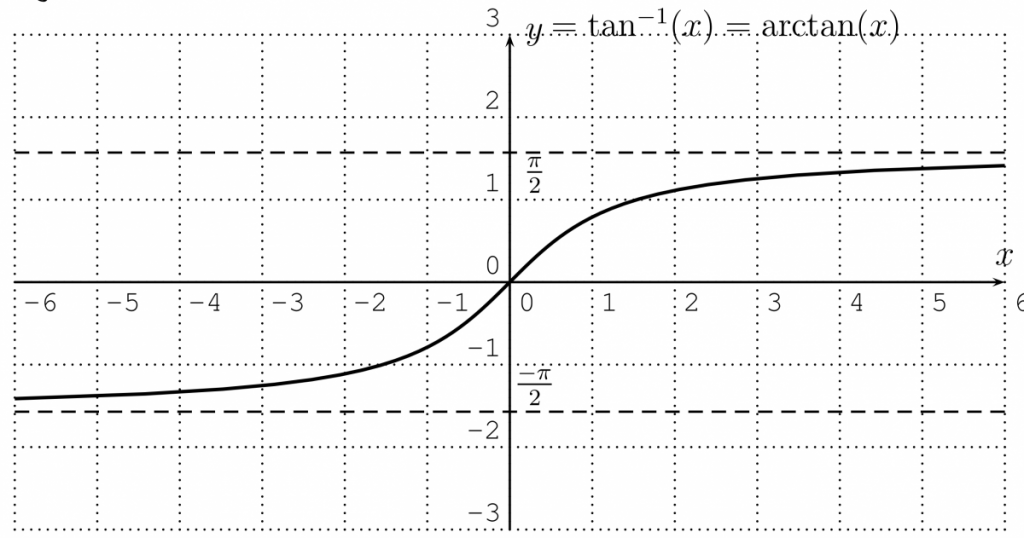
Observation: The inverse tangent is an odd function, so $\tan^{-1}(-x)=-\tan^{-1}(x)$
(recall that a function $f(x)$ is odd provided $f(-x)=-f(x)$)
Example 19.1 Recall the exact values of the tangent function from Chapter 17:
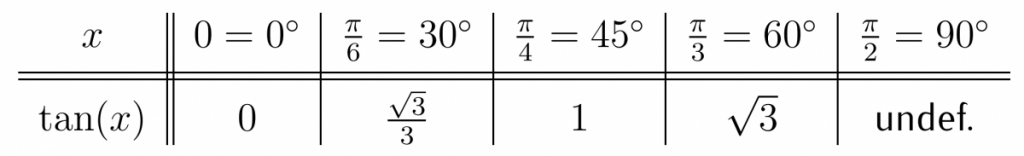
Use the table and Observation above to find exact values of the inverse tangent function. Give answers in both degrees and radians.
a. $\arctan(1)$ b. $\arctan\left(-\frac{\sqrt{3}}{3}\right)$. c. $\tan^{-1}(0)$
VIDEO: The Inverse Tangent Function – Definition and Example 19.1
THE FUNCTION $\sin^{-1}(x)$
Consider the graph of the function $y=\sin(x)$. It is not one-to-one either:
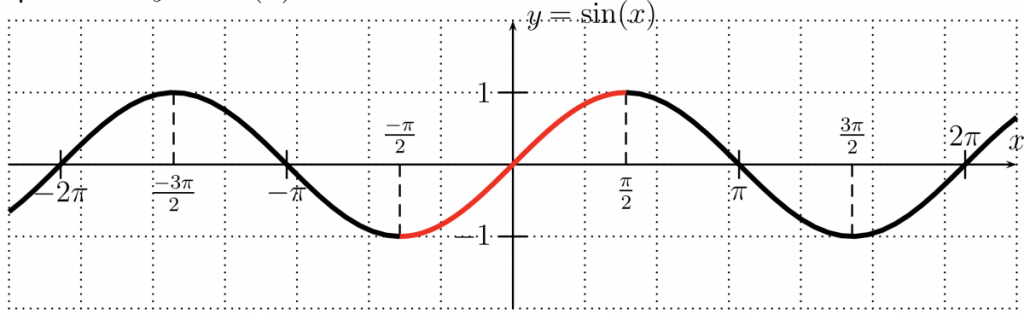
However, if we restrict the function to the interval $\left[-\frac{\pi}{2},\frac{\pi}{2}\right]$ (shown in red) the resulting function is one-to-one, and so we can consider the inverse function.
Definition 19.5. The inverse of the function $y=\sin (x)$ with restricted domain $D=\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$ and range $R=[-1,1]$ is called the inverse sine or arcsine function. It is denoted by
$y=\sin ^{-1}(x) \quad \text { or } \quad y=\arcsin (x) \quad \Longleftrightarrow \quad \sin (y)=x, \quad y \in\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$
The arcsine reverses the input and output of the sine function, so that the arcsine has domain $D=[-1,1]$ and range $R=\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$.
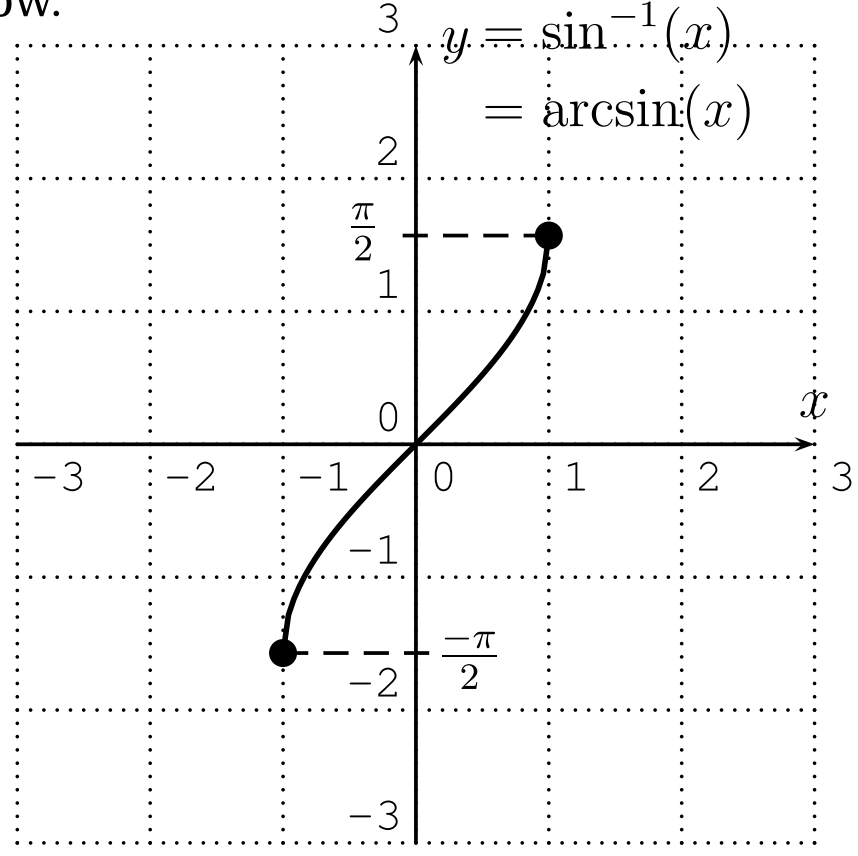
Observation: The inverse sine function is an odd function, so $\sin^{-1}(-x)=-\sin^{-1}(x)$.
Example 19.7. Recall the values of the sine function for common angles:
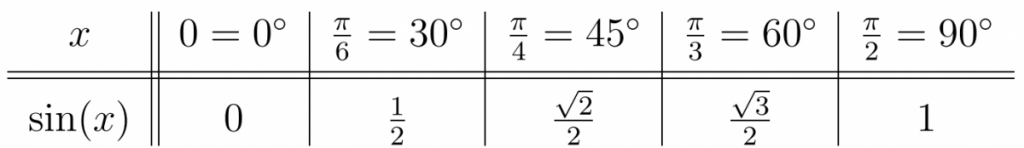
Use the Table and Observation above to find exact values of the arcsine function. Give answers in both degrees and radians.
a. $\sin ^{-1}\left(\frac{\sqrt{2}}{2}\right)$, b. $\sin^{-1}(1)$, c. $\sin^{-1}(0)$, d. $\sin ^{-1}\left(\frac{-1}{2}\right)$, e. $\sin^{-1}(3)$
VIDEO: The Inverse Sine Function – Definition and Example 19.7
THE FUNCTION $\cos^{-1}(x)$
We treat the function $\cos(x)$ similar to $\sin(x)$. However, we are no longer able to use the interval $\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$. Why?

In order to make the cosine function one-to-one, we restrict to the interval $[0,\pi]$.
Definition 19.8. The inverse of the function $y=\cos (x)$ with restricted domain $D=[0, \pi]$ and range $R=[-1,1]$ is called the inverse cosine or arccosine function. It is denoted by
$y=\cos ^{-1}(x) \quad \text { or } \quad y=\arccos (x) \quad \Longleftrightarrow \quad \cos (y)=x, \quad y \in[0, \pi]$
The arccosine reverses the input and output of the cosine function, so that the arccosine has domain $D=[-1,1]$ and range $R=[0, \pi]$.
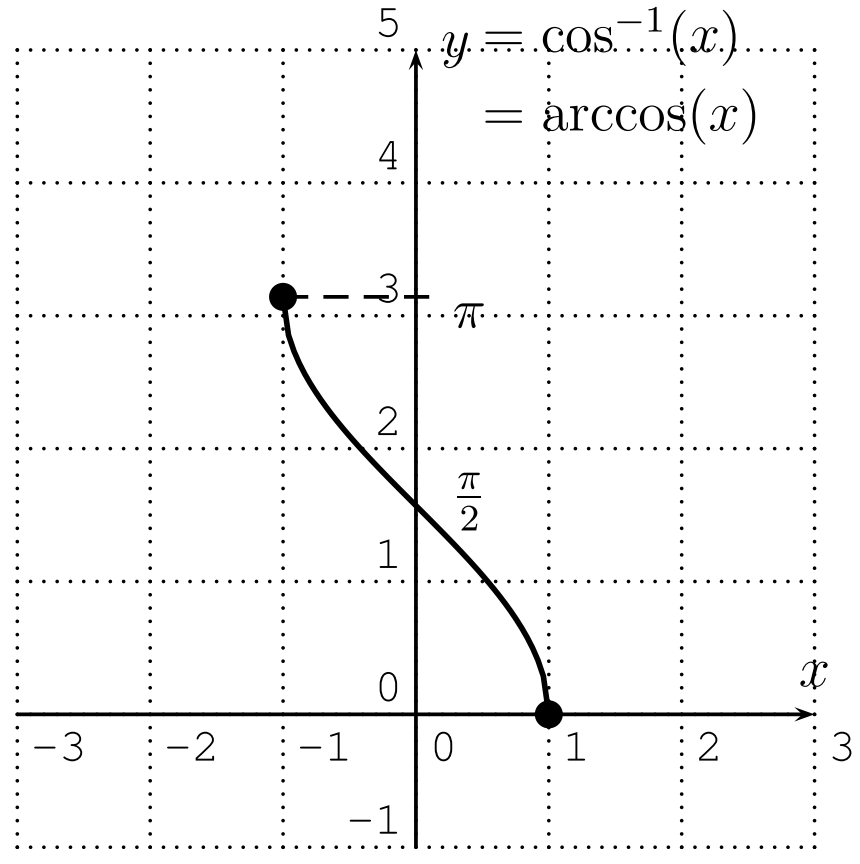
Observation: The arccosine function is neither even nor odd. However, it does obey the following symmetry: $\cos^{-1}(-x)=\pi-\cos^{-1}(x)$
(in many problems, you can avoid the use of this formula by remembering the unit circle definition of cosine).
Example 19.10. Recall the values of the cosine function for common angles:
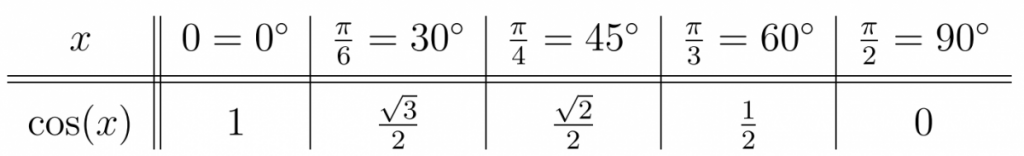
Use the Table and Observation above to find exact values of the arccosine function. Give answers in both degrees and radians.
a. $\arccos\left(\frac{\sqrt{3}}{2}\right)$, b. $\cos^{-1}(1)$, c. $\cos ^{-1}(0)$, d. $\arccos=\left(-\frac{1}{2}\right)$, e. $\arccos(2)$
VIDEO: The Inverse Cosine Function – Definition and Example 19.10
Inverse trig functions on the TI-84+ calculator
How do we find values of inverse trig functions that don’t appear in our “common angles” table?
Example. Find the values of the inverse trig functions using a calculator. Include at least 5 decimal digits past the decimal point.
a. $\arccos(0.35)$ (in radians)
b. $\tan^{-1}(-13.2)$ (in degrees)
VIDEO: Inverse trig functions on the calculator
RECALL: Converting between radians and degrees
$\text{radians}=\text{degrees}\cdot\frac{\pi}{180}$
$\text{degrees}=\text{radians}\cdot\frac{180}{\pi}$




Thank you so much for the lecture! Except for the fact that we want to substrate arccos(x) from pi to get arccos(-x), everything seems natural and fine.
However, I wonder if we need a calculator for the coming actual exams. I am a bit worried since I don’t have the calculator.
Plus, in the case of the practice exam, I confused its date and I missed it. I will make sure not to happen again!
Thank you!
Oh, I will use the one you used for the lecture!
One more thing. I have a problem with Trigonometry – Inverse Functions: Problem 1 on the website.
I thought the answers below are..
2. Evaluate arccos(sqrt 3/2):
in radians: pi/6
in degrees:30
4. Evaluate arcsin(sqrt2/2):
in radians: pi/4
in degrees: 45
But both were not correct. I have no idea on Q 2 and somehow answer for Q 4 were negative value. I don’t know where I got wrong. Can I please get help?
Hi Suim,
Great to hear from you! With regards to the WeBWorK, YOUR ANSWERS ABOVE ARE CORRECT in problem #1 for both part 2 and part 4 (there is a bug in that WeBWorK problem, I have notified our bug-fixer). Nice catch!
With regards to the exam, you will need a calculator of some kind – as long as it can evaluate trig functions and inverse trig functions I think you will be fine.
I hope this answers your questions – if not, feel free to reply here…
-Prof. Reitz
prof, chapter 8 to 12 doesn’t have the trig function or am I wrong because if so then I will be confused, please let me know.
Hi Raoul,
You’re right, Chapter 8-12 does NOT have trig functions (or logarithms, or exponential functions). They will appear on the following exam (Exam #3), but you don’t have to worry about them for this exam (Exam #2).
-Prof. Reitz
Hello Prof. Reitz,
I know I email you for help and before you can help me I send an email 2 or 3 hours later saying I’ve found out how to solve my problem but this time I actually have not the slightest idea of how to do this and I can’t find anything regarding this anywhere. Please I need help. I sent an email with a picture of the problem.
No problem – I’m happy to help, I’ll check my email and get back to you there.
-Prof. Reitz
Hey Prof.Reitz,
I just uploaded my work to the dropbox folder, but some of the numberings got cropped out and I don’t know if that’s a problem or if it will confuse you. Not all the numbers got cropped out but most of them did. Is that going to be an issue, should I resend it again
Hi Lauwens! First, thanks for uploading your work in a timely fashion – that’s great. It would make my grading life easier if you resubmitted it with the numbers visible (since your work was already submitted on time, you will not be penalized for submitting it late). Thank you!
Prof. Reitz
I sent it again is this a bit better
Thanks!