Hi everyone! This is the second of our distance-learning lessons. Read through the material below, watch the videos, and send me your questions.
NEW THIS WEEK: Daily Quiz & Attendance. There will be a short quiz each class day. Complete the quiz before the end of the day to be marked present for today’s class (the quiz should appear below this post).
Lesson 13: Exponential and Logarithmic Functions
Lesson Date: Tuesday, March 24th.
Topic: This lesson covers Chapter 13 in the book, Exponential and Logarithmic Functions.
WeBWorK: There are two WeBWorK assignments on today’s material, due next Tuesday 3/31:
Exponential Functions - GraphsandLogarithmic Functions - Graphs.
Lesson NOtes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Exponential Functions and their Graphs
We’ve been living in the world of Polynomials and Rational Functions. We now turn to exponential functions. These functions are “very natural” – that is, they show up in the real world – but they are also more complicated than Polynomial and Rational functions (for example, an exponential function grows more quickly than any Polynomial)
The spread of coronavirus, like other infectious diseases, is modeled by exponential functions.
Definition. An exponential function is a function of the form $f(x)=c\cdot b^x$, where $b$ and $c$ are real numbers and $b$ is positive ($b$ is called the base, $x$ is the exponent).
Example 1 (Textbook 13.2): Graph the exponential functions $f(x)=2^x, g(x)=3^x, h(x)=10^x, k(x)=\left(\frac{1}{2}\right)^x, l(x)=\left(\frac{1}{10}\right)^x$.
Now let’s see what happens when we change the number $c$ in $y=c\cdot b^x$.
Example 2 (Textbook 13.6): Graph the exponential functions
a) $y=2^{x}, \quad$ b) $y=3 \cdot 2^{x}, \quad$ c) $y=(-3) \cdot 2^{x}, \quad$ d) $y=0.2 \cdot 2^{x}, \quad$ e) $y=(-0.2) \cdot 2^{x}$
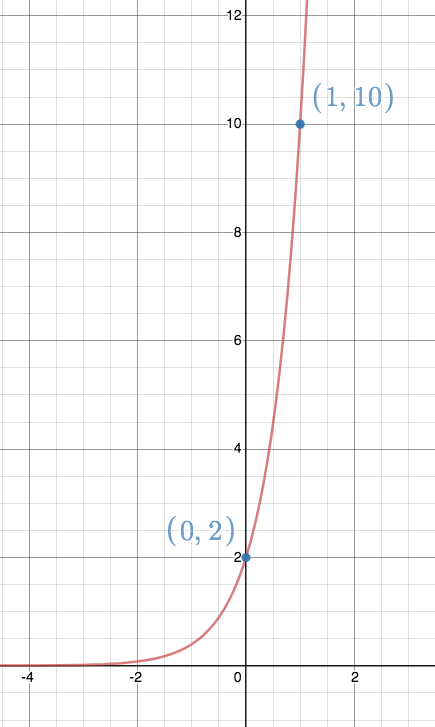
Example 3: The graph below shows an exponential function $f(x)$. Find a formula for $f(x)$.
Logarithmic Functions and their Graphs
Definition. If $b$ is a positive real number and $b\neq 1$, then the logarithm with base $b$ is defined:
$y=\log_b(x) \iff b^y=x$
What does the definition of logarithm mean? The idea is that the logarithm is the inverse function of the exponential function. Let’s look at an example.
Question: Is an exponential function one-to-one? (What does one-to-one means).
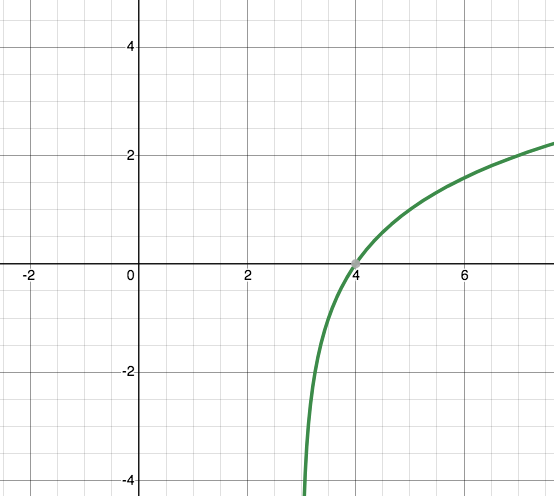
Example 4. The graph below shows the function $y=\log_2(x)$ but shifted to the right 3 units. Find a formula for the function in the graph.
That’s it for now! Take a look at the WeBWorK assignment, leave your questions below (or use the Ask for Help button in WeBWorK, or send me an email) and don’t forget to complete Quiz#1.
Best of luck,
Prof. Reitz




Hello professor Reitz I have a question from the first video which is about the asymptotes.
Hello professor Reitz I have a question from the first video which is about the asymptotes.
Hi Mark,
Sorry for the late reply! Happy to answer a question – let me know what it is…
Prof. Reitz
log(10.000) how did you get log10 .
Hello professor Reitz I have a question of the topic of Logarithmic Functions and their Graphs, on question E where did you get the log10 from?
[latexpage]
Hi Mark,
It’s just a special rule – when we don’t write down a base, it means the log is base 10. So anytime you see something like $\log (10,000)$, you can mentally insert the “base 10” and think of it as $\log_{10} (10,000)$.
This is one of two special logarithms (the other one, written $\ln$, means $\log_e$, the log in base $e$.
-Prof. Reitz
Thank you so much professor.