MAT1275 College Algebra and Trigonometry, Spring 2017

Topics:

• Discussion of homework problems on solving radical equations, p. 538 #22, 24, 38, 40, 42

Once again, emphasizing that when checking the answers, we need to distinguish the times that the checking fails because we made an error somewhere, from the times that the checking fails because our method gives so-called “extraneous solutions” sometimes. See notes last time.

• More on complex numbers:

Definition of a complex number

Real and imaginary parts of a complex number

Operations on complex numbers

The operations on complex numbers work basically like normal algebra, except that in a complex number does not represent a variable, but rather , so every time we get a power of  higher than the first power we must simplify it using .

Also, to divide complex numbers, we are actually rationalizing the denominators. But in this case, the product of a complex number and its conjugate is always a positive real number, so it works out even more nicely – we never get negative numbers as denominators.

Homework:

• Review the radical equation homework problems we discussed in class. Make sure that you understand how to tell when you have made an error (and need to go back and correct it) versus when you have an “extraneous solution” that needs to be thrown out.

• Review the definition of complex number, real part, and imaginary part

• Review the operations on complex numbers. Addition and subtraction should not be any trouble at all: in multiplying or dividing (rationalizing denominators) you just need to remember that .

• Do the assigned problems from the Course Outline in section 6.8

• Do the WeBWorK: due by Sunday 11 PM, but do not wait to the last minute!

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

Topics:
• More on solving radical equations
• What if a “solution” does not check?
• Introduction to complex numbers: imaginary numbers

Examples we worked in class:

• Pairs worked on the second problem in this document: MAT1275RadicalEquations.
One new thing that happened here, which we had not seen before in the examples, was that we ended up having to solve a quadratic equation after squaring both sides, so there were two candidates for solutions to the equation.
When we checked the two proposed solutions in the original equation, only one of them worked. The other one (it was 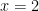) would have worked if the radical sign allowed us to take the negative square root: as I have mentioned several times, this is a symptom of the fact that 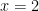is what is sometimes called an “extraneous solution”, and it must be excluded from our final answer to this problem. [What happened here is related to our discussion of solving from last time.]

• I worked Example 4 from Section 6.7 in the textbook. Here we had to isolate the radical term first. Please note that we did not completely isolate the radical (although we could have done that): it is only necessary to isolate the term which contains the radical, so that when we square both sides, there will be no radical left. For more study, here are notes in which I solve this equation be completely isolating the radical, and I also show you what happens if you try to square both sides without isolating the radical.

In this example, we also ended up solving a quadratic equation along the way, which gave us two candidates for solution to the original equation, and again only one of them worked when we went to check. This is what happened when we went to check the other one:

Look very carefully at what happened here. If we could have taken the negative square root of 81,  the next-to-last step would have read

21 – 18 = 3

which is true. Remember that is a symptom of the fact that this proposed solution (y=21) is  an “extraneous solution” generated by our solution method, not that we made any error, but rather that the solution method itself sometimes gives extra garbage along with any solutions of the original equation that exist. When checking, we need to look for this and rule such things out.

• Pairs then worked on the Skill Practice problem

Solve

Several points emerged when discussing the student solution that was put on the board: please make sure that you understand them! Here is our complete discussion.
The solution on the board originally gave two values for m, namely &latex m=1$ or . The first one worked when it was checked in the original equation. However, when we substituted into the original equation, we got

– so this proposed solution does not check. But is it an “extraneous solution”? NO! Notice that even if we would have been allowed to take the negative square root of 1, this still would not have checked: We would have gotten   at the last step. The reason that this proposed solution did not check is that the student made an error while solving the problem: the factorization used to solve the quadratic equation was incorrect. We had to go back and correct that factorization, and after we did that, we got two proposed solutions which both checked out. So there are actually two solutions to the original equation – namely, 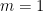or .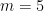

Here are the important points to take away from this (and the previous) examples:

• The method we use to solve equations containing radical expressions will always give any solutions of the equation that exist, but it may also give other numbers as well (sometimes called “extraneous solutions”, but I prefer to just call them “garbage”.) We must check (it’s not just a good idea, it’s the law!) in order to exclude these “garbage solutions” from our final answer. [This is similar to what happens in the case of rational equations.]

• The symptom of a proposed solution being a “garbage solution” which must be excluded, is that when we go to check it in the original equation, it would have worked if the radical sign allowed us to take the negative square root.

• If the proposed solution fails even if we take the negative square root, it means that we made a mistake somewhere and we must go back and correct that mistake! In general, if any proposed solution in any type of equation fails to check, our first thought should be that we may have made an error somewhere and we should carefully check all our work.

• There are two types of equations we have studied in this course for which the solution methods we use can generate “garbage solutions” in addition to any genuine solutions that exist. They are:

rational equations – the symptom is that the proposed solution gives a 0 denominator

radical equations – the symptom is that the proposed solution would work if the radical sign gave the negative square root instead of the positive square root

For any other type of equation in this course, if a proposed solution fails to check, it means that there is an error somewhere.

• In particular, any time we solve an equation by factoring, it is an excellent idea to check the factorization by multiplying it out. Incorrect factoring is a very frequent cause of errors and it is well worth taking the minute or so to check every factorization before proceeding.

• In the cases of solving rational equations or solving radical equations, it is possible that all, some, or none of the proposed solutions will survive to be genuine solutions of the original equation. Anything can happen. It is necessary to check each and every proposed solution in the original equation, and watch for the symptoms of its being a garbage solution which has to be eliminated. If all of the proposed solutions are garbage, the equation has no solutions (and that is our final answer).

New topic: introduction to complex numbers

We have previously said that the square root of a negative real number is not a real number, and we were careful not to say that it is undefined. The reason can now be revealed: it is possible to define square roots of negative real numbers, but those square roots will not be real numbers themselves. We must invent a new type of number in order to do this. They will be called imaginary numbers, even though they are no less real than the real numbers.

Definition:

This is the principal square root of -1. Its name is 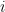. (In other words, 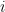is not a variable! it is simply the name of this number, just as 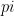is the name of a number.) Make sure that you write your  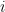so that it cannot be mistaken for either the number 1 or the letter l.

There is another square root of -1, namely .

Because 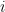 is a square root of -1, it follows that

(Remember, this is the definition of square root.)

To define the square root of any negative real number:

If 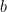is any positive real number,  then we define

Examples:

Please note the order in which we write those final results. In general, we write numerical factors before the 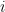, but radical factors after it, just as we do with variables. Make sure you understand the reasons for this!

Homework:

• Review the examples of solving radical equations that we discussed in class. I have left out the details of the two problems you worked in pairs, so that you can re-work them yourselves (and you should do so!) Make sure that you understand all of the points we made in discussing these problems and what happened when we checked them.

• Do the following problems from the Course Outline: section 6.7, p.547 starting with problem 22 (the problems before that have already been done in class or assigned as homework);

• Do section 6.8, p. #11-16 all (this is not in the Course Outline)

• Do the WeBWorK: due by Sunday 11 PM, but do not wait to the last minute!

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

(after Test 1)

Topics: (from Section 6.7 in the textbook)

• Introduction to Radical Equations

• Solving radical equations, part 1

Our method for solving radical equations is as follows:

• First, isolate the radical (if necessary)

• Then square both sides of the equation, using the fact that

– this is just the definition of the square root!

•  Then solve the resulting equation

• And finally, check all solutions in the original equation to see if they are genuinely solutions or not (and of course, to see if we made any errors!)

The reason that we need to check in solving radical equations (it’s not just a good idea, it’s the law!) is because of the following phenomenon:

Suppose we want to solve

We should realize at the beginning that there is no solution to this equation, because the radical sign tells us to take the principal square root, which cannot be a negative number. But suppose that (as we too often do) we just mechanically go on working this problem without realizing that. So we try squaring both sides of the equation:

But this does not solve the original equation: when we go to check, we get

?

The problem is that when we squared both sides of the equation, we lost the information that the left-hand side of the equation represented a non-negative real number, but the right-hand side was negative. After squaring, both sides became positive.

Notice that would work if the radical sign allowed us to take a negative number square root. This is the “symptom” that shows that this is what is sometimes referred to as an “extraneous solution” – that is, it is not a solution at all, but just something extra that our method generated.

(A similar thing causes problems when we solve rational equations. There, when we clear the denominators, we are multiplying both sides of the equation by the same thing, namely the LCM of all the denominators. This is fine as long as the thing we are multiplying by is not 0, but the problem is that we don’t know whether or not the LCM is 0 because it has a variable in it! So in that case the “symptom” of the alleged solutions that ended up having to be thrown away is that they led to a 0 denominator when we went to check.)

I worked out Example 1 and Exercises 14 and 16 from Section 6.7 in class, not forgetting to check before reporting the final results.

Homework:

• Review the examples discussed in class, including the one included in these notes.

• Do the following from the textbook: p. 547 #11, 12, 13, 15, 21, 22

• Also do (simplifying radical expressions, including rationalizing the denominator) from the Course Outline, the assigned problems from Section 6.6 (starting on p. 538)

• Do the WeBWork: some of this your should have already started and it is due by tomorrow 11 pm (but don’t wait to the last minute!) There is also a new assignment on radical equations which is not due until Sunday night: you should try to do at least the first 4 problems of that one by Wednesday’s class.

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

Please keep checking back for the posts with notes/assignments from the class meetings this week. I am working on them, but in the meantime…

There are some WeBWork  assignments, some due by Sunday evening (I extended them) and make sure that you do them because that material is also on Test 1! The rest is not due until Tuesday evening, but don’t wait to the last minute!

Reminder: Please make sure to read this page on the WeBWorK policies for this class.

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

Test 1 is scheduled for the first 50 minutes or so of class on Monday 6 March. Please see the Course information sheet for policies related to tests.
Here are two self-tests showing the material that will be covered on Test 1. Use them to test yourself.

MAT1275Test1ReviewSpring2017

Here are the answers: please note that the work has not been shown in these, but you will be graded on your work! Therefore, make sure that you also check the sections/examples listed below to make sure that you are using correct methods for the problems.

MAT1275Test1ReviewAnswersSpring2017

Review sections/examples for each problem:

Self-Test A

1) See Section  4.1 Examples 1-6 and MAT1275ExponentsDefinitionsLaws

2) See Section 5.4 Complex Fractions  Examples 1-2 (Method I) Examples 3-5 (Method II)

3) See Section 5.4 Complex Fractions  Examples 1-2 (Method I) Examples 3-5 (Method II)

4) See Section 5.3

5) See Section 5.3

6) See Section 5.5

7) See Section 5.5

8) See Section 6.1

9) See Section 6.3

10) See Sections 6.1, 6.3

Self-Test B

1) See Section 5.4 Complex Fractions  Examples 1-2 (Method I) Examples 3-5 (Method II)

2) See Section 5.4 Complex Fractions  Examples 1-2 (Method I) Examples 3-5 (Method II)

3) See Section  4.1 Examples 1-6 and MAT1275ExponentsDefinitionsLaws-Condensed.pdf

4) See Section 5.3

5) See Section 5.3

6) See Section 5.5

7) See Section 5.5

8) See Section 5.5

9) See Sections 6.1, 6.2 (Rational Exponents) – make sure that you compute this by first translating into exponent/root notation, as in Example 2 of Section 6.2

10) See Sections 6.1, 6.2 (Rational Exponents)  – make sure that you compute this by first translating into exponent/root notation, as in Example 2 of Section 6.2

Topics:

• Discussion of homework: distinguishing changing to a common denominator from clearing denominators: when do we use each one, and why, and how we do them. Please make sure that you know and understand the difference and can describe what you are doing using these terms! Also we stressed that the division line in a rational expression is also a grouping symbol, so it is very important that you extend it to the right length. Notice how we draw the division lines when we have complex fractions. The grouping is essential!

• Roots and radicals: see below for definitions, vocabulary, and important theorems

Definitions:

square roots:

b is a square root of a

n-th roots (where n is a natural number):

b is an n-th root of a 

Vocabulary:

Considering n-th roots,

n is called the index or degree of the root.

The sign is called the radical sign.

The quantity under the radical sign is called the radicand.

Notation: in all of these, represents  a real number.

represents the principal square root of (the positive square root), if is a positive real number. The other square root will be .

represents the principal n-th root of . Notice that the index is placed inside the angle of the radical sign: it is very important that you write it there and not in front of the radical sign!

There are two cases:

• If n is an even natural number, and is a positive real number, then there are two n-th roots of , and  is the positive n-th root (just as in the case of the square root). The other n-th root will be .

• If n is an odd natural number, then for any real number , there is exactly one n-th root of , and it is represented by .

It is always true that  for any natural number index n.

Theorem: (NOT a definition, despite what your textbook says!)

For any real number x,

if n is an odd natural number

BUT

if n is an even natural number

Illustration: (this is to show why the theorem is true – it’s not a proof, but a “proof”)

Suppose we take x to be  -4

Then by carefully following the order of operations (and recalling that the radical sign is also a grouping symbol, so any operation in the radicand has to be done before we take the root) we can compute the following:

for the odd index 3,

so we get back -4 in the end,

BUT for the even index 2,

, which is , not -4 itself!

BE CAREFUL!

Take a look at Example 5 in section 6.1 to see how the Theorem is used to simplify various radical expressions.

Homework:
• Review the examples and homework problems discussed in class. Make sure that you understand when and why we need to change to a common denominator, and when and why we clear denominators. Also make sure that you understand and can correctly use all of the vocabulary and notation!
• Do the assigned problems from section 6.1 from the Course Outline, only up to #37!
• Do the WeBWork – The assignment has two parts, both due by next Sunday evening, but don’t wait to the last minute!

Reminder: Please make sure to read this page on the WeBWorK policies for this class.

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

Topics:
• Solving equations with rational expressions by clearing the denominators (section 5.5) – I discussed Examples 1, 2, and 5 and we worked in pairs on the homework exercises 9, 13, and 17.

As we saw, when solving an equation which contains the variable in a denominator, it is necessary to check any candidate solutions to make sure that they do not cause a 0 denominator. Such “solutions” are not solutions of the original equation, and must be eliminated.

Vocabulary:
Rational expression
Complex fraction
Lowest common multiple (or Least common multiple)
Change to a common denominator
Clear a denominator

Homework:
• Reminder: Make sure that you have done all the things in the checklist! (Should already have been done!)
• Review the examples and homework problems discussed in class. Make sure that you understand when and why we need to change to a common denominator, and when and why we clear denominators.
• Do the assigned problems from section 5.5 from the Course Outline
• Do the WeBWork – due by next Tuesday evening, but don’t wait to the last minute!
• Don’t forget that Monday is a holiday, so we do not meet.

Reminder: Please make sure to read this page on the WeBWorK policies for this class.

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

Topics:
• More practice simplifying complex fractions
We worked in pairs on the example in these notes, done two ways: MAT1275ComplexFractions

Make sure that you understand how each of the two methods works and that you can use both methods fluently. As promised, I have snipped out the textbook pictures of the example of Method II (and I’ve added one of their examples of Method I: it is posted on the Piazza discussion board.
• This blog, WeBWorK, and Piazza – we found this blog and logged on to WeBWorK and explored it a bit.
Homework:
• Please see this checklist (separate post) and make sure that you have caught up with everything on it by the next time we meet!
• Review the example we worked in class. Make sure that you understand how the two methods for simplifying a complex fraction work, and that you can describe how to do them in a few words. We will be seeing complex fractions again later in the course!
• Do the homework problems from the Course Outline on Complex Fractions (p. 487) if you have not already done them.
• Do the WeBWorK, starting with the Orientation assignment at least to problem #8, before you do the rest. The deadline is Tuesday 11 PM, but start early! Do not wait to the last minute!

Please make sure to read this page on the WeBWorK policies for this class.

Remember that you can use the Piazza discussion board to ask questions if you get stuck on any of the WeBWorK or the other homework problems. Don’t forget to include the problem itself in your question, as that will make it easier for you to get a quick response!

WeBWorK has been set up for this course. The WeBWorK is here. (This is the corrected link.)

Please follow these instructions: MAT1275WeBWorKinformation-Spring2017 in order to log in. After changing your password and entering your citytech email (if it is not already there), you may start on the Orientation assignment to get used to how WeBWorK works.

A common problem that occurs when people try to log in using iPhone is that there is automatic capitalization for the first letter when you type in your username or password. Check to make sure the capitalization is turned off (or turn it off) while you type!

Important: there are two people who areexceptions to the rule given in those notes as to how your username is formed. In general, the username is your first initial followed by your last name (or last names), all in lowercase, no spaces or punctuation.

The exceptions for this class are: There are two people who are brothers who both have the same first initial: your username is your entire first name followed by your last name, all in lowercase.

The following people need to enter their citytech email addresses in their WeBWorK User Information:

Edin Metovic

For all other students, your citytech email address is already there, so DO NOT CHANGE IT. You MUST have your citytech email in WeBWorK or the “email your instructor” will not work.

AFTER you’ve done at least 7-8 of the Orientation problems, you should start on the assignments which are due by next Tuesday evening 11 PM. Don’t wait to the last minute!

——

Also, for those of you for whom I already have citytech email addresses, an invitation to join the Piazza discussion board has been sent to you at that address by The Piazza Team. Please look for that invitation and follow the instructions to log on to Piazza, if you have not already done so. If you have already joined Piazza, there is no need to join again. (I will send invitations to the others once I have your citytech email addresses!

——

NOTE: The post for today’s class is delayed while I was working on getting this set up. Please look for it sometime tomorrow (Thursday).

In addition to the tutors in the Learning Center in AG-18, we have math specialists who are available to help you. Here is the information and schedule:

PerkinsGrantTutoring 2017