(after Test 3)
Topics:
• The inverse trig functions $\sin^{-1}(x)$, $\cos^{-1}(x)$, and $\tan^{-1}(x)$: definitions and notation
• Solving right triangles using the inverse trig functions
Definitions and how to read the notation:
Note: the superscript -1 in these functions’ names represents the inverse function. It is very important that you remember that this is not the -1 power.
$\sin^{-1}(x)$ is read as “the inverse sine of x” or “the arcsine of x” (which literally means “the arc whose sine is x”). I like to read it as “the angle whose sine is x”.
An infinite number of angles (arcs on the unit circle) can have the same sine x. The inverse sine picks out the one angle which is between $-90^{\circ} = \pi$ and $90^{\circ} = \pi$ (inclusive).
Definition: $\sin^{-1}(x) = y \iff \sin(y) = x$ and $-90^{\circ} \le y \le 90^{\circ}$
Note that the sine of an angle must be between -1 and 1 (inclusive), therefore $\sin^{-1}(x)$ is only defined for x which is between -1 and 1 (inclusive). If you try to find $\sin^{-1}(2)$, for example, on your calculator, you will get an error message because it is undefined.
similarly:
$\cos^{-1}(x)$ is read as “the inverse cosine of x” or “the arc-cosine of x” (which literally means “the arc whose cosine is x”). I like to read it as “the angle whose cosine is x”.
An infinite number of angles (arcs on the unit circle) can have the same cosine x. The inverse cosine picks out the one angle which is between $0^{\circ} = 0$ and $180^{\circ} = 2\pi$ (inclusive).
Definition: $\cos^{-1}(x) = y \iff \cos(y) = x$ and $0^{\circ} \le y \le 180^{\circ}$
Note that the cosine of an angle must be between -1 and 1 (inclusive), therefore $\cos^{-1}(x)$ is only defined for x which is between -1 and 1 (inclusive). If you try to find $\cos^{-1}(2)$, for example, on your calculator, you will get an error message because it is undefined.
$\tan^{-1}(x)$ is read as “the inverse tangent of x” or “the arctangent of x” (which literally means “the arc whose tangent is x”). I like to read it as “the angle whose tangent is x”.
An infinite number of angles (arcs on the unit circle) can have the same tangent x. The inverse tangent picks out the one angle which is between $-90^{\circ} = \pi$ and $90^{\circ} = \pi$ (not inclusive).
Definition: $\tan^{-1}(x) = y \iff \tan(y) = x$ and $-90^{\circ} < y < 90^{\circ}$
$\tan(x)$ can be any real number, therefor there is no restriction on the values of x for $\tan^{-1}(x)$.
Homework:
• Review the example we discussed in class. (My WeBWorK problem)
• Do the WeBWorK assignments. It is recommended that you do them in the following order:
(1) Unit Circle (from last time)
(2) Graphing Sine Cosine (also from last time)
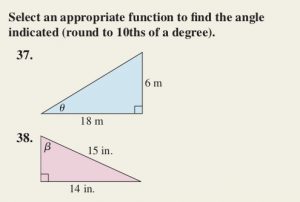
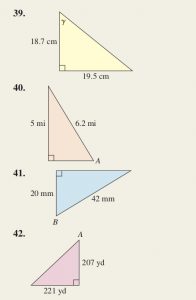
(3) Solving Right Triangles – Inverse Trig
• Here are problems (including the promised problems from Coordinate Plane Definition) from the textbook which you may put on the board at the start of class next time:
On the coordinate plane definition of the trig functions:
Find the values of the six trig functions of $\theta$ if this point is on the terminal side of the angle:
(1) (-6, 8)
(2) (5, -12)
(3) (-7, -7)
From the Trig textbook:
Remember that if you get stuck on any of the problems or have a question about any of the material, you can post a question to the Piazza discussion board.
In case you prefer to view videos on any of these topics, Here is a copy of the Course Outline with links to video resources for each topic.
