I .Do Now: read the following problem. https://www.desmos.com/calculator/ecnyow98r1
Marry has decided to plants some flowers, so she can make packet money. She will spend up to $180 for the seeds. One rose seeds cast $15, one peony seeds cost $5. She has enough space for plant 16 flowers. She wants to plants at lest 3 peonies and at lest 8 roses. If peonies earn$40 for her and the roses earn $60. how many of each type should marry to plant to maximize the amount of packet money she can make?
1. From the problem, list all the constraints:
- She will only spend up to $180 for the seeds.
- she has space only for 16 flowers.
- she wants plant at lest 3 peonies and 8 roses
2. Find variables:
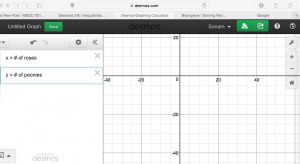
let x = # of roses and let y = # of peonies
II. Use Desmos to solve the problem by turning all the constraints into Inequalities.
1. Turn the first two boxes of Desmos Graphing Calculator into a text boxes.
Type in our variables x = # of roses and let y = # of peonies
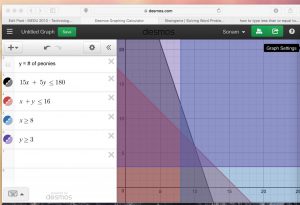
2. Turn the all constraints into inequalities and type then into the boxes of Desmos Graphing Calculator.
- 15x + 5y ≤ 180
- x + y ≤ 16
- y ≥ 3
- x ≥ 8
3. Turn everything into same color, that will make the region that we’re looking for a little bit more clear, because it just the darkest region.
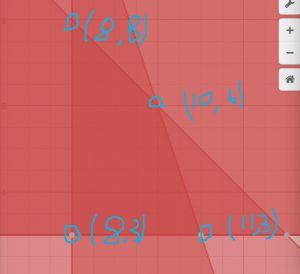
4. The four sets of intersection of the darkest region are the sets that satisfied of our constraints.
- (10,6)
- (11,3)
- (8,3)
- (8,8)
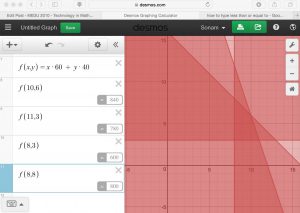
III. Solve the problem by set up a function with two variables x and y.
- f(x,y) = x(60) + y(40)
- Plug the four sets into the function.
- f(10,6) = 840
- f(11,3) = 780
- f(8,3) =600
- f(8,8) = 800
IV. Conclusion :
As you can see when x = 10 and y = 6, Marry can make the maximum of money $840. So she should plants 10 roses and 6 peonies.




Leave a Reply