The following problems come from Arthur Kramer’s Fundamental of Technical Mathematics, second edition. With permission from Professor Kramer and from the Math Department Curriculum Committee, I will request these problems be adapted for the appropriate WeBWorK homework sets in MAT 1275. If anyone has comments, further requests, or suggestions, please let me know.
-
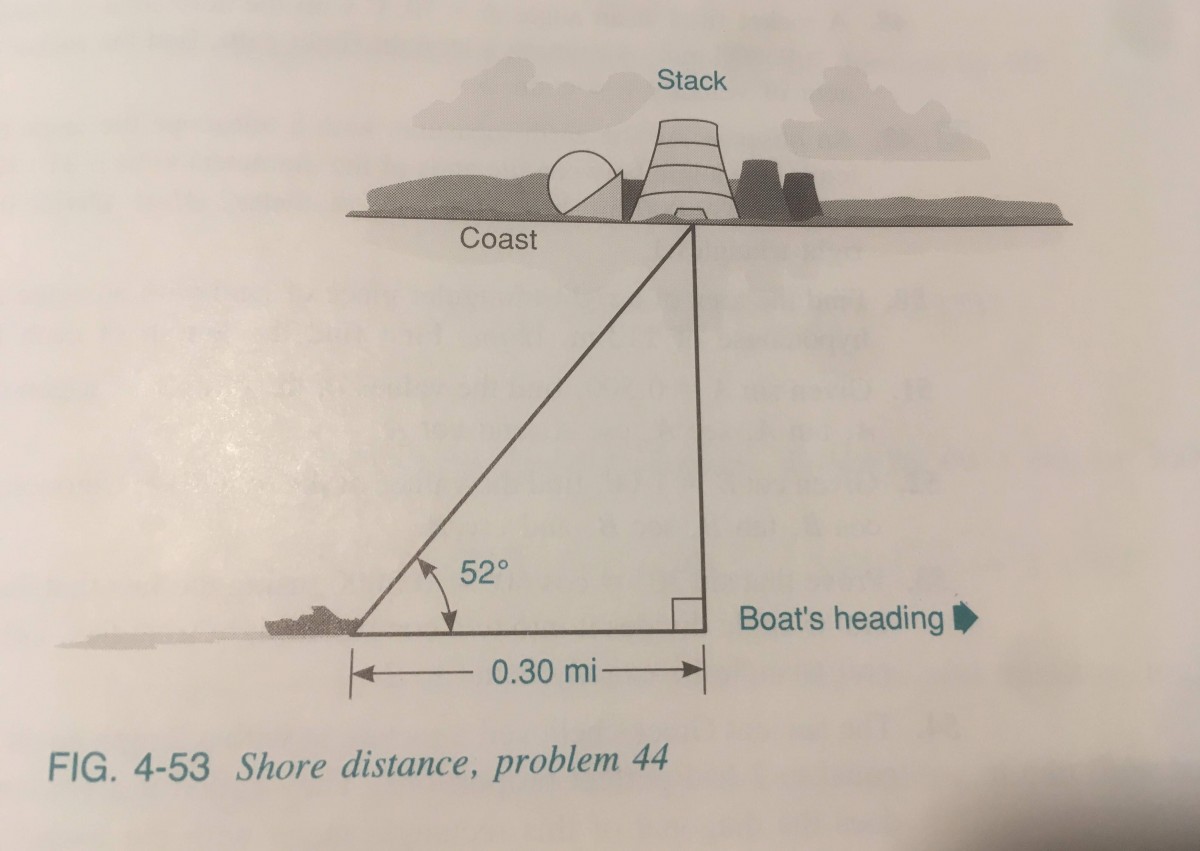
page 166 #44 (figure page 167)
Enrique is traveling parallel to a straight coastline in his motorboat and wants to find his distance from the shore Using a compass, he takes the bearing of the stack of a power plant and measures the angle between his heading and the stack to be 52 degrees. After he travels 0.30 mi, the angle between his heading and the stack is 90 degrees. How far is he from the coast?
-
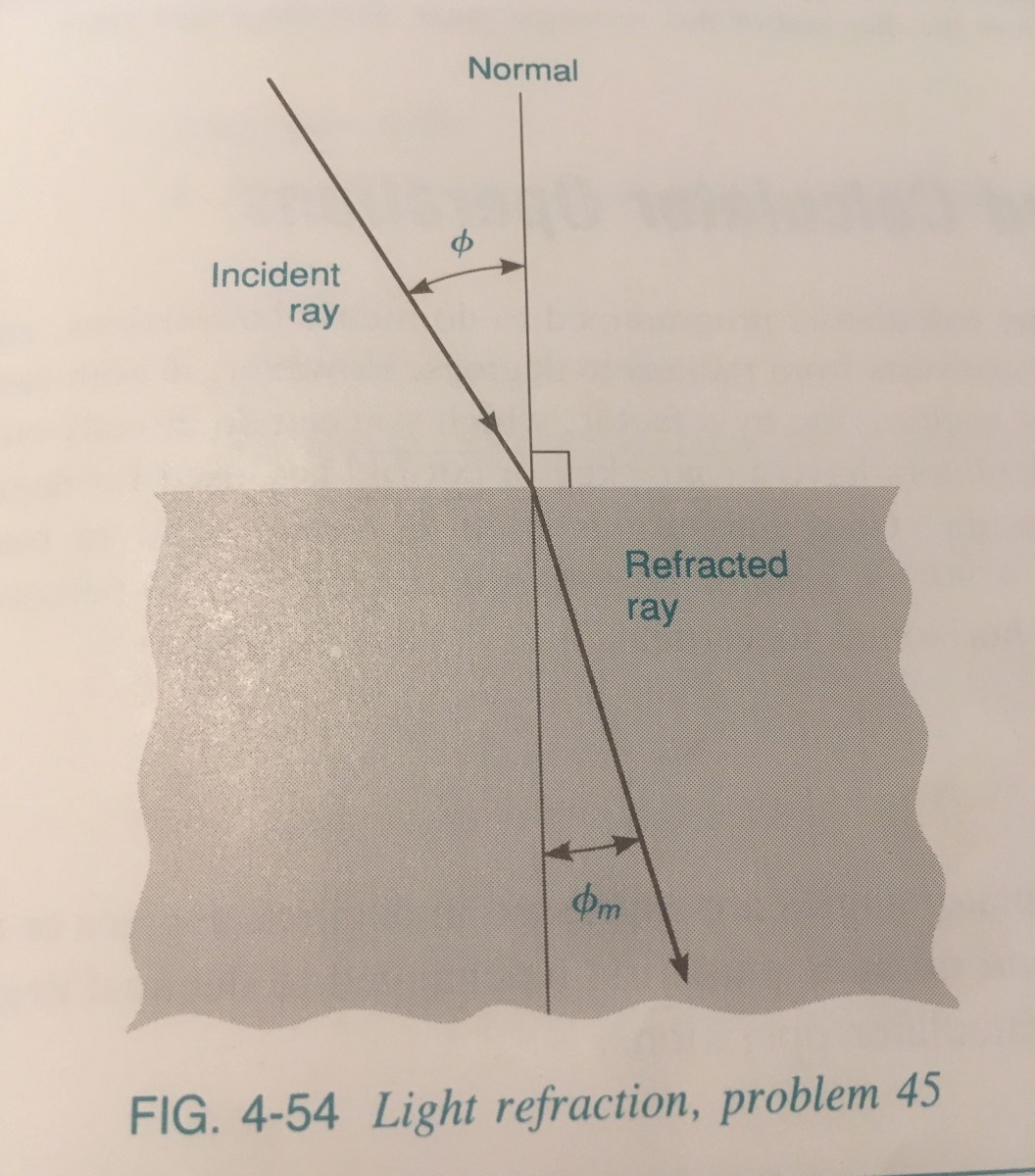
page 166 #43 (figure page 167)
The index of refraction of a medium is defined as the ratio of the speed of light c in air to the speed of light c_m in the medium. It is equal to:
\[\mu=\frac{c}{c_m} = \frac{\sin(\phi)}{\sin(\phi_m)}\]
where $\phi$ is the angle of incidence and $\phi_m$ is the angle of refraction of a light ray. If a ray of light passes from air into water, where $\mu = 1.33$ and $\phi = 0.254$ rad, find the angle of refraction $\phi_m$ in radians.
-
Adapted from Example 5-17 page 197 (figure page 197)
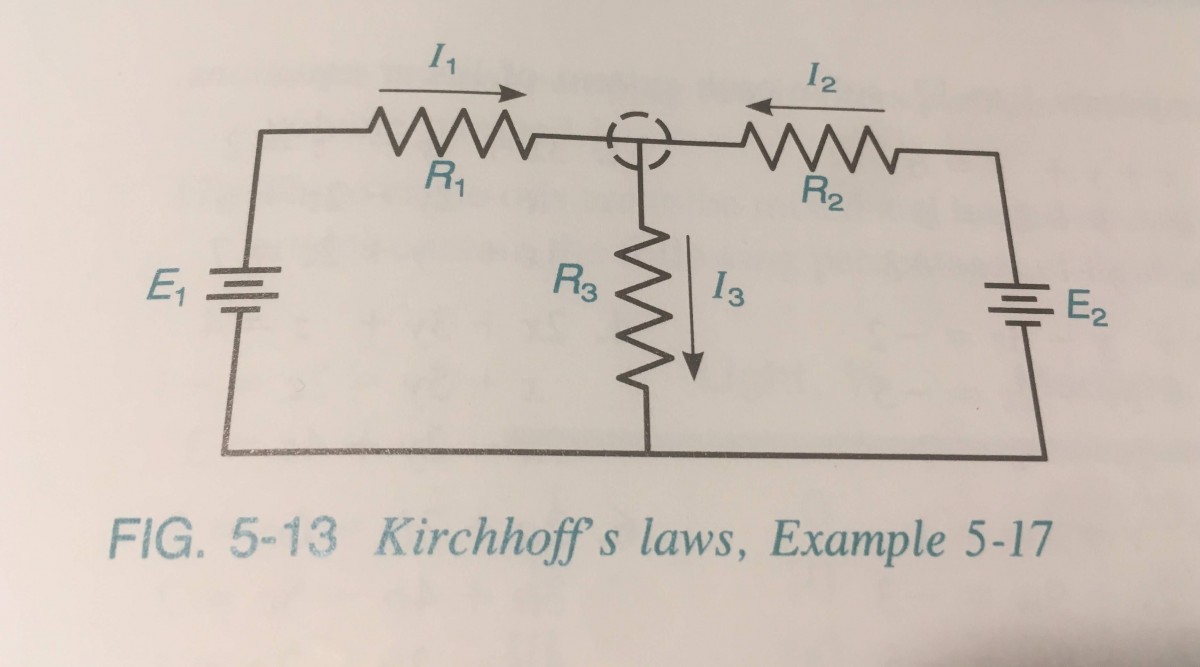Kirchoff’s laws for the circuit in the figure yield the following three linear equations\[ I_1 + I_2 -I_3 =0 \]
\[I_1 R_1 + I_3R_3 = E_1\]
\[I_2 R_2 + I_3R_3 = E_2\]
where $E_1$ and $E_2$ represent voltage, $R_1, R_2$, and $R_3$ represent resistances, and $I_1, I_2$, and $I_3$ represent current.
Let $E_1 = 14.0 V, E_2 = 12.6 V, R_1 = 6.00 \Omega, R_2 = 5.50 \Omega$, and $R_3 = 4.00 \Omega$. Find $I_1, I_2$, and $I_3$.
-
The earth’s orbit around the sun and the moon’s orbit around the earth are approximate circles of radii $1.5 \times 10^8$ and $3.8 \times 10^5$, respectively, where the sun is at the center of the earth’s orbit and the earth is at the center of the moon’s orbit. If the sun is placed at the origin of a coordinate system, what is the equation of moon’s orbit when the center of the earth is
(a) on the positive $x$ axis and
(b) in the first quadrant on the line $y=x$?
-
Page 284 #98
The velocity $V$ of a small water wave is given by:
\[ V = \sqrt{\frac{\pi}{4 \lambda d}} + \sqrt{\frac{4 \pi}{\lambda d}}.\]
Simplify and combine the terms, expressing $V$ with a rational denominator.
Recent Comments