Multiplying and dividing rational expressions (for review!)

1. $⊳$ Monomials (5:55)  This video uses function notation 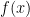and analyzes the expressions as functions.

[Example 1] ${\displaystyle \frac{6x^3}{5}}\cdot {\displaystyle \frac{2}{3x}}$

[Example 2] ${\displaystyle \frac{2x^4}{7}}÷{\displaystyle \frac{5x^4}{4}}$

2. $\star$  Multiply and divide rational expressions   Multiply the following monomials and determined if the result is defined when $b=0$.  ${\displaystyle \frac{-5b^3}{6}}\cdot {\displaystyle \frac{3b^2}{-10}}$ .

3. $⊳$ Multiply rational expressions (4:51)  Multiply ${\displaystyle \frac{a^2–4}{a^2–1}}\cdot {\displaystyle \frac{a+1}{a+2}}$  noting that $a\ne -2$ and $a\ne -1$.

4. $⊳$ Dividing rational expressions (4:09) Divide ${\displaystyle \frac{2p+6}{p+5}}÷{\displaystyle \frac{10}{4p+20}}$ where $p\ne -5$.

5. $\star$ Multiplying rational expression practice  ${\displaystyle \frac{4z^2+24z}{3z^2–9z-12}}\cdot {\displaystyle \frac{z^2–4z-5}{z-4}}$

6. $⊳$ Mulitply and expressing as a simplified rational expression  (3:37) Multiply ${\displaystyle \frac{3x^{2}y}{2ab}}\cdot {\displaystyle \frac{14a^{2}b}{18x{y}^2}}$  where $a,b,x,y\ne 0$.

7.  $\star$ Divide the rational expressions and simplify  ${\displaystyle \frac{10n^2+23n–5}{4n^2+6n}}÷{\displaystyle \frac{25n^2–10n+1}{7n+3}}$