1. Adding and Subtracting rational expressions with like denominators (3:45) This video contains one example of adding and one of subtracting rational expressions, namely:
[Example 1]
[Example 2]
2. Practice: Adding and subtracting rational expressions with like denominators. Problems similar to: 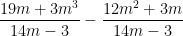 . (4 problems)
. (4 problems)
3. Adding rational expressions with unlike denominators (2:43) .
4. Practice: Adding rational expressions with unlike denominators. Problems similar to . (4 problems)
5. Adding rational expressions: unlike denominators (5:11) Problems such as .
6. Subtracting rational expressions: unlike denominators (4:47) Solving .
7. Practice: Adding rational expressions with unlike denominators. Problems such as . (4 problems)
8. Finding the least common multiple of two integers (4:15)
[Example 1] Find the of 36 and 12.
[Example 2] Find the of 12 and 18 (uses the prime factorization method).
9. Finding the least common multiple with repeating factors (2:34) Find the .
10. Practice: Find the least common multiple of two integers. Find the . (4 problems)
11. Finding the least common multiple of polynomials (6:51)
Finds the least common multiple of and .
12. Subtracting rational expressions (4:48) 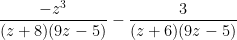 .
.
13. Practice: Combine the rational expressions. Problems such as (4 problems)
. (4 problems)
.
. (4 problems)
.