Hi everyone! Read through the material below, watch the videos.
Lesson 22: Vectors in the plane
Topic: This lesson covers Chapter 22: Vectors in the plane.
WeBWorK: There are four WeBWorK assignments on today’s material:
Vectors – Components
Vectors – Operations
Vectors – Magnitude and Direction
Vectors – Unit Vectors
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Introduction to Vectors
Today we will be working with the plane $\mathbb{R}^2$, but looking at things in a slightly different way – instead of points (which have only a location), we will be focussing on vectors (which have a magnitude (size) and direction). This change in perspective is quite powerful, and brings to light many useful features of the plane – but in practice, you will find it similar to the work we did in the previous lesson on polar form of complex numbers.
Definition 22.1. A geometric vector in the plane is a geometric object in the plane $\mathbb{R}^{2}$ that is given by a direction (angle) and magnitude (size). We denote a vector by $\vec{v}$ (it is written by some authors as $v$ ), its magnitude is denoted by $||\vec{v}||,$ and its directional angle by $\theta$.
Vectors are often drawn as directed line segments $\vec{v}=\overrightarrow{P Q}$. Two such segments represent the same vector if they have the same magnitude and direction.
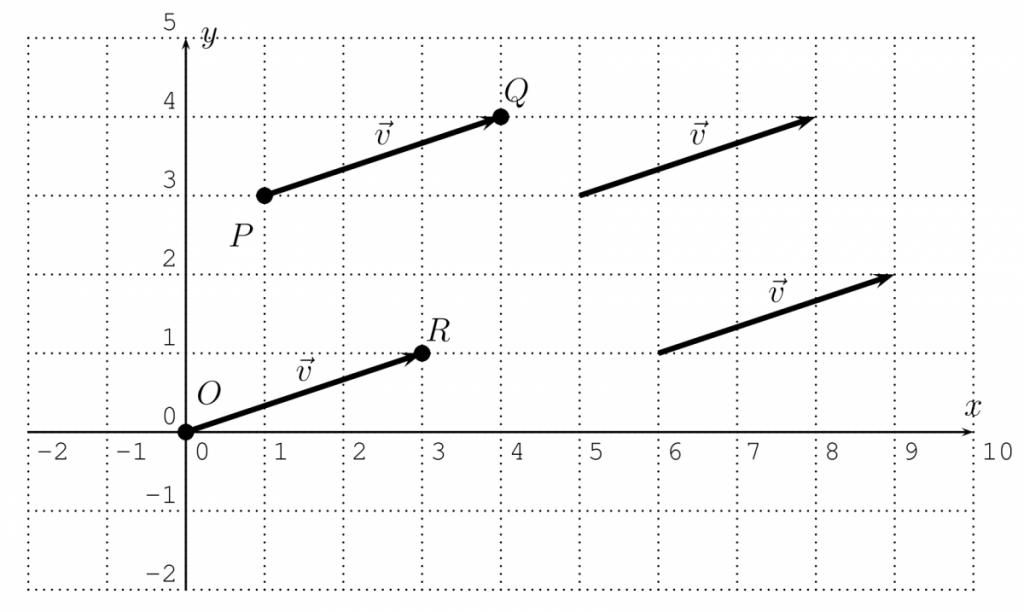
We can always represent a vector $\vec{v}$ by arranging the starting point of $\vec{v}$ to be the origin $O(0,0)$ (as in $\overrightarrow{O R}$ in the picture above). If $R$ has coordinates $R(a, b)$ then we also write for $\vec{v}=\overrightarrow{O R}$:
$\vec{v}=\langle a, b\rangle$, or $\vec{v}=\begin{bmatrix} a\\ b\end{bmatrix}$
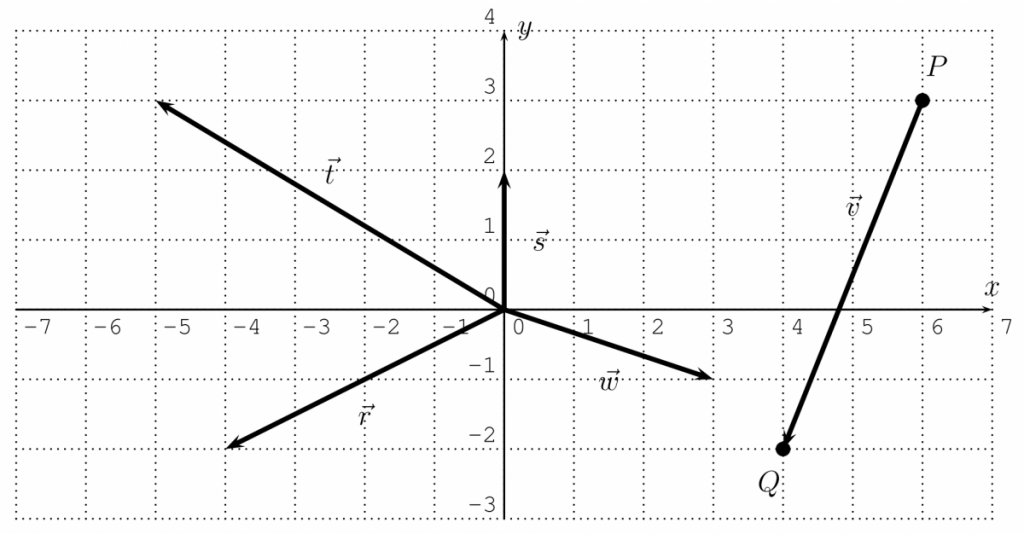
Example 22.2. Graph the vectors $\vec{v}, \vec{w}, \vec{r}, \vec{s}, \vec{t}$ in the plane, where
$\vec{v}=\overrightarrow{P Q}$ with $P(6,3)$ and $Q(4,-2),$ and
$\vec{w}=\langle 3,-1\rangle, \quad \vec{r}=\langle-4,-2\rangle, \quad \vec{s}=\langle 0,2\rangle, \quad \vec{t}=\langle-5,3\rangle$
The formulas for magnitude and directional angle of a vector are the same as those for modulus (magnitude) and argument (angle) of a complex number:
Formulas for magnitude and angle of a vector: Suppose $\vec{v}=\langle{a,b}\rangle}$ is a vector in the plane $\mathbb{R}^2$. Then the magnitude and angle of $\vec{v}$ are given by:
$||\vec{v}||=\sqrt{a^2+b^2}$, $\tan(\theta)=\frac{b}{a}$
Conversely, we can obtain the coordinates of a vector from its magnitude and directional angle by:
$\vec{v}=\langle||\vec{v}|| \cdot \cos (\theta),||\vec{v}|| \cdot \sin (\theta)\rangle$
Example 22.4. Find the magnitude and directional angle of the given vectors:
a) $\langle-6,6\rangle$
b) $\langle 4,-3\rangle$
c) $\langle-2 \sqrt{3},-2\rangle$
d) $\langle 8,4 \sqrt{5}\rangle$
e) $\overrightarrow{P Q}$, where $P(9,2)$ and $Q(3,10)$
VIDEO: Intro to vectors, finding magnitude and direction – Example 22.4
Operations on Vectors
There are two basic operations on vectors, scalar multiplication and vector addition.
Scalar Multiplication
Definition 22.5. The scalar multiplication of a real number $r$ with a vector $\vec{v}=\langle a, b\rangle$ is defined to be the vector given by multiplying each coordinate by $r$:
$r \langle a, b\rangle =\langle r \cdot a, r \cdot b\rangle$
Example 22.6. Multiply, and graph the vectors
a) $4 \cdot\langle-2,1\rangle$
b) $(-3)\cdot\langle-6,-2\rangle$
VIDEO: Scalar multiplication of vectors – Example 22.6
Observation. When we multiply a vector $\vec{v}$ by a positive real number $r>0$, the result will have the same angle as $\vec{v}$, while the magnitude will be stretched by a factor of $r$.
The Unit Vector
Definition 22.8. A vector $\vec{u}$ is called a unit vector if it has a magnitude of 1
$\vec{u}$ is a unit vector $\quad \Longleftrightarrow ||\vec{u}||=1$
There are two special unit vectors $\vec{i}$ and $\vec{j}$, which are the vectors pointing in the $x-$ and the $y$ -direction.
$\vec{i}=\langle 1,0\rangle \quad \text { and } \quad \vec{j}=\langle 0,1\rangle$
Example 22.9. Find a unit vector in the direction of $\vec{v}$
a) $\langle 8,6\rangle$
b) $\langle-2,3 \sqrt{7}\rangle$
VIDEO: Unit vectors – Example 22.9
Vector Addition
The second operation on vectors is called vector addition.
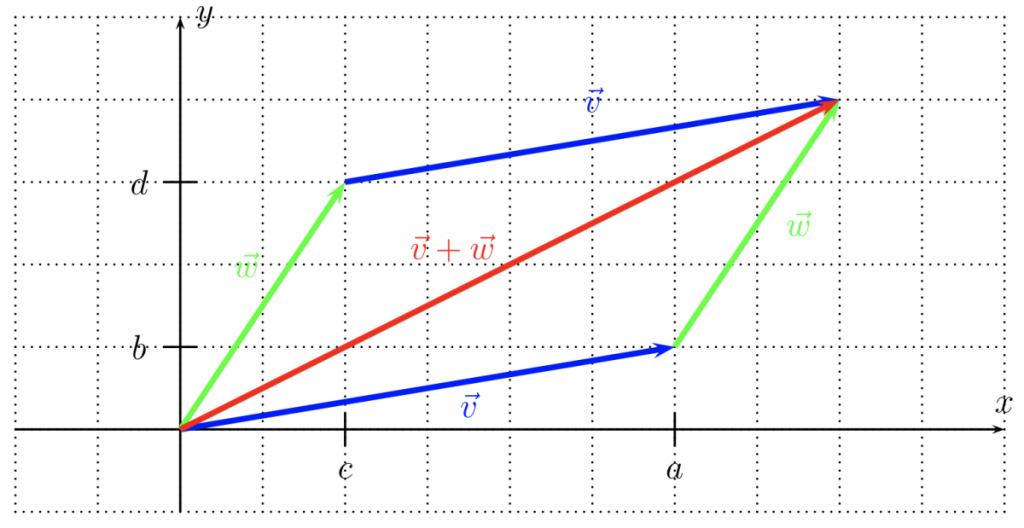
Definition 22.10. Let $\vec{v}=\langle a, b\rangle$ and $\vec{w}=\langle c, d\rangle$ be two vectors. Then the vector addition $\vec{v}+\vec{w}$ is defined by component-wise addition:
$\langle a, b\rangle+\langle c, d\rangle:=\langle a+c, b+d\rangle$
In the plane, this corresponds to starting at the origin, following $\vec{v}$ and then $\vec{w}$ (or vice versa, following $\vec{w}$ and then $\vec{v}$). In the picture, note that whichever path you take from the origin you will still arrive at the same point in the upper right, $\vec{v}+\vec{w}$:
Example 22.11. Perform the vector addition and simplify as much as possible.
a) $\langle 3,-5\rangle+\langle 6,4\rangle$
b) $5 \cdot\langle-6,2\rangle-7 \cdot\langle 1,-3\rangle$
c) $4 \vec{i}+9 \vec{j}$
d) find $2 \vec{v}+3 \vec{w}$ for $\vec{v}=-6 \vec{i}-4 \vec{j}$ and $\vec{w}=10 \vec{i}-7 \vec{j}$
e) find $-3 \vec{v}+5 \vec{w}$ for $\vec{v}=\langle 8, \sqrt{3}\rangle$ and $\vec{w}=\langle 0,4 \sqrt{3}\rangle$
VIDEO: Vector addition – Example 22.11
Example 22.12. The forces $\vec{F}_{1}$ and $\vec{F}_{2}$ are applied to an object. Find the resulting total force $\vec{F}=\vec{F}_{1}+\vec{F}_{2}$. Determine the magnitude and directional angle of the total force $\vec{F}$. Approximate these values as necessary. Recall that the international system of units for force is the newton $\left[1 N=1 \frac{k g \cdot m}{s^{2}}\right]$
a) $\vec{F}_{1}$ has magnitude 3 newtons, and angle $\theta_{1}=45^{\circ}$
$\vec{F}_{2}$ has magnitude 5 newtons, and angle $\theta_{2}=135^{\circ}$
b) $\left|\vec{F}_{1}\right|=7$ newtons, and $\theta_{1}=\frac{\pi}{6},$ and $\left|\vec{F}_{2}\right|=4$ newtons, and $\theta_{2}=\frac{5 \pi}{3}$
VIDEO: Vector addition application (force) – Example 22.12
That’s it for now – give the WeBWorK a try!


