Table of Contents
Hi everyone! Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Lesson 13: Exponential and logarithmic functions
Topic. This lesson covers Chapter 13: Exponential and Logarithmic Functions.
Learning Outcomes.
- Graph basic exponential and logarithmic functions.
- Understand the definition of logarithms and their connection to exponents.
- Make connections between algebraic and graphical properties of exponential and logarithmic functions.
WeBWorK. There are two WeBWorK assignments on today’s material:
- Exponential Functions – Graphs
- Logarithmic Functions – Graphs
Lesson Notes (pdf):
Additional Video Resources.
Question of the Day: What kinds of functions can we use to describe the spread of an infectious disease like COVID-19?
Exponential Functions and their Graphs
We’ve been living in the world of polynomials and rational functions. We now turn to exponential functions. These functions are “very natural” – that is, they show up in the real world – but they are also more complicated than polynomial and rational functions (for example, an exponential function grows more quickly than any polynomial).
Definition. An exponential function is a function of the form $f(x)=c\cdot b^x$, where $b$ and $c$ are real numbers and $b$ is positive ($b$ is called the base, $x$ is the exponent).
Example 1 (Textbook 13.2): Graph the exponential functions $f(x)=2^x, g(x)=3^x, h(x)=10^x, k(x)=\left(\frac{1}{2}\right)^x, l(x)=\left(\frac{1}{10}\right)^x$.
VIDEO: Example 13.2 – graphs of exponential functions with different bases
Now let’s see what happens when we change the number $c$ in $y=c\cdot b^x$.
Example 2 (Textbook 13.6): Graph the exponential functions
a) $y=2^{x}, \quad$ b) $y=3 \cdot 2^{x}, \quad$ c) $y=(-3) \cdot 2^{x}, \quad$ d) $y=0.2 \cdot 2^{x}, \quad$ e) $y=(-0.2) \cdot 2^{x}$
VIDEO: Example 13.6 – graphing exponential functions, multiply by a constant
Example 3: The graph below shows an exponential function $f(x)$. Find a formula for $f(x)$.
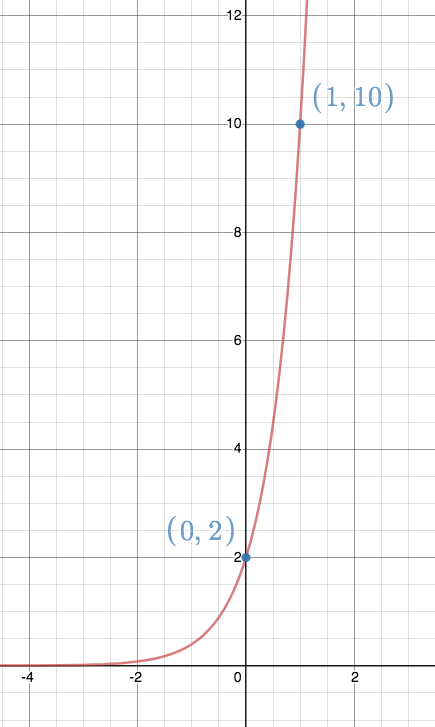
VIDEO: Example 3 – finding the formula of an exponential function from the graph
Logarithmic Functions and their Graphs
Definition. If $b$ is a positive real number and $b\neq 1$, then the logarithm with base $b$ is defined:
$y=\log_b(x) \iff b^y=x$
VIDEO: Introduction to Logarithms
What does the definition of logarithm mean? The idea is that the logarithm is the inverse function of the exponential function. Let’s look at an example.
Question: Is an exponential function one-to-one? (What does one-to-one mean?).
VIDEO: What does the definition of logarithm mean?
Logarithms as inverse functions.
Example 4. The graph below shows the function $y=\log_2(x)$ but shifted to the right 3 units. Find a formula for the function in the graph.
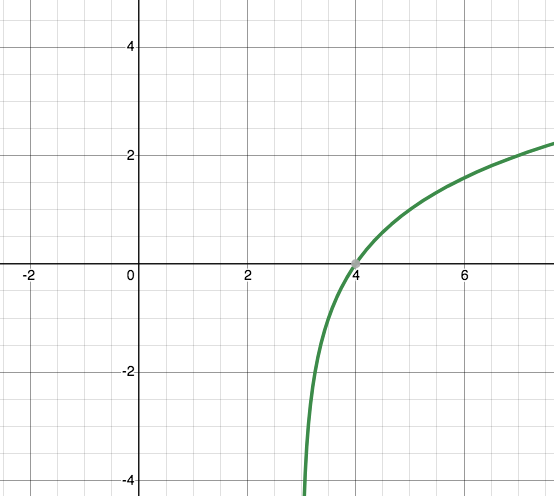
VIDEO: Example 4 – Transformations of log functions
Exit Question
Find a formula for the function $y=\log_2(x)$ if it is shifted to the left 2 units and up 5 units.
Answer
$y=\log_2(x+2)+5$
Good job! You are now ready to practice on your own – give the WeBWorK assignment a try. If you get stuck, try using the “Ask for Help” button to ask a question on the Q&A site.


