One of the topics we discussed at our December meeting was symmetry of functions. This topic is covered in MAT 1375 when students are learning about graphing functions, but it may appear in any course that includes functions of real numbers and their graphs.
Even or odd or….???
One issue that sometimes gives students trouble is the language that is used. An integer is either even or odd, but a function is either even or odd….or neither even nor odd! This difference between how the words are used to describe integers and how they’re used to describe functions can be really hard to process, since even and odd are such familiar concepts for integers. This difference also obfuscates a really important feature of functions: that most of them are neither even nor odd! Symmetry is a really special feature for a function to have; if you try to think of a random function, odds are that you’ll come up with one that does not have any symmetry. (Pun intended.)
Add to this the fact that there are other names that some people use instead of even and odd. An even function is said to have symmetry with respect to the y-axis and an odd function is said to have symmetry with respect to the origin. Some instructors might prefer to say y-axis or origin symmetry instead of even or odd, which can be easier for students in some ways, but harder as well because they often expect that if the first one’s called y-axis symmetry, shouldn’t the second one be called x-axis symmetry? These names do have the advantage, however, that they describe the features of a graph of a function with symmetry; really the names should be symmetry with respect to reflection in the y axis and symmetry with respect to rotation of 180 degrees about the origin, but these don’t quite have the same ring as even and odd do.
So one of the tutor’s challenges is to manage all these possibilities. Students might arrive at the ALC with any number of these words rattling around in their heads, so tutors should do their best to determine which language a student’s instructor is using, and stick to it. (The textbook uses the even and odd terminology, so that’s a good first guess.)
The formal definition
All of these potential complications occur even before a student encounters the formal definition of these properties. Whatever names you choose, the formal definition can be another stumbling block for students, who might be intimidated by something that looks like this:
- A function
is called even if
for all
.
- A function
is called odd if
for all
.
I’ve found that students can start to get a grasp of what this definition means if they can see it being used in specific examples. This can be approached in a few ways. For example:
- With graphs
- With formulas
Tutors can probe what students already know about even and odd functions by asking leading questions like, “Draw a graph of an even function” or, “Give an example (in function notation) of an odd function.” The two approaches above should complement one another and tutors will likely be required to present both, along with the relationship between them. Some students are more visual and can understand the property graphically, while others struggle with graphs, but can manipulate symbols in the formulas with ease. In either case, it should be emphasized that something is going on with signs. I typically begin with the graphical approach since I consider it a little easier for more students.
Understanding the definition graphically
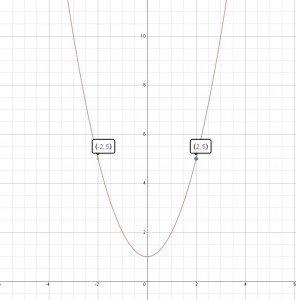
I start with even functions because there’s only one negative sign to contend with. This is the graph of a function and two particular points on the graph: and
. Ask the student to compare the
-coordinates of the two points. Then ask them to compare the
-coordinates of these points. Their answers should reflect that the
-coordinates differ by a sign, but the
-coordinates are equal. Ask what it means for two points to have the same
coordinate (they’re at the same height). Ask what it means for two points to have
-coordinates that differ by a sign (they’re the same distance from the
-axis, but on opposite sides of it.) So these points are related by a reflection in the
-axis. Check that the same is true of another pair of related points, and another, and another, and so on. Emphasize that since every such pair of points is related in this way, the graph is of an even function. Give students a few graphs of different functions and have them determine whether the graphs represent even functions.
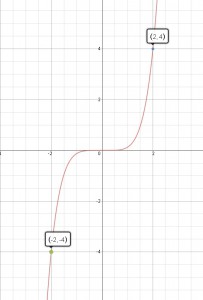
Odd functions can be introduced graphically as well, but now there are two negative signs. The points and
are shown on the graph of this function. Now when you ask students to compare the
– and
-coordinates, they should describe the sign difference in each. Ask again what it means for two points to have
-coordinates that differ by a sign (they’re the same distance from the
-axis, but on opposite sides of it.) Ask what it means for two points to have
-coordinates that differ by a sign (they’re the same distance from the
-axis, but on opposite sides of it.) So these points are related by two reflections, one in each axis. Typically we describe them as instead being related by a 180 degree rotation about the origin. Again, select a few other pairs of related points and emphasize that the property holds for all such pairs; that’s what makes this the graph of an odd function. Give students a few graphs of different functions and have them determine whether the graphs represent functions that are even, odd, or neither even nor odd. Emphasize that most functions are neither even nor odd by sketching several graphs.
Understanding the definition with formulas
Students who are visual learners may understand the concept intuitively after a graphical description, but they may still struggle with actually checking the symmetry of a given function. It’s good here for them to see several examples. Again, emphasize that the point of this is to see what the signs tell us.
One potential problem is that a student has trouble with function notation, and needs practice evaluating a function at something other than a number. Try substituting nonsense symbols first. For example if
, then
. At this point, instruct them to treat
as a nonsense symbol. It’s helpful to include parentheses here because another pitfall for students is forgetting them when they’re needed, and then having incorrect signs. Keeping track of signs is the only thing that matters here, so try to keep students from making sign errors at every stage. If a student appears to have an issue performing this substitution, have him/her practice substituting
for
in a few different functions
before asking about symmetry.
Once the correct substitution has been made to write down , what remains is simplifying the expression and checking to see if what’s left is
, $-latex f(x)$, or neither of these. Often this is where a student stumbles; it’s easy to remember to perform the substitution, but harder to remember what you’re supposed to do with it. It’s easy to forget what this is all about! At this point, the tutor should ask leading questions instead of giving the student the answer. Refer the student to the formal definition again. They’ve figured out the left-hand-side of the two equations listed in the definition. Their job is to check whether it looks like the right-hand-side of either equation. Sometimes, even if a student understands this in theory, it’s hard for them to put it into practice for a specific function. The tutor should give them an easy first example of a function that ends up being even, this way, the tutor can ask whether the right-hand-side looks like
and the answer will be yes. If even that gives a student trouble, have him/her write down
again to compare. Have the student determine whether a few different example functions are even or not even before discussing odd functions. Emphasize that if a function is not even, that does not mean that it’s odd.
It can be easier for a student to determine whether a function is odd if he/she has already determined that it’s not even. Again, a student might freeze before knowing what algebraic manipulation to perform to determine whether a function is odd. It’s helpful here that students are used to looking for common factors. Really wheat you want them to do is to determine whether their simplified has
as a factor. If he/she is not immediately able to recognize whether the
has
as a factor, have him/her write down what
looks like to compare. Again, have the student determine whether a few different example functions are even, odd, or neither even nor odd.
Revealing patterns
At December’s meeting we discussed the symmetry of a few examples in detail. The examples we focused on were all rational functions, but we could have chosen other classes of examples to discuss too. The conversation centered around patterns that emerge. For example, in a rational function where the numerator and denominator are both odd functions, the rational function is even:
.
Some students like to have patterns like this spelled out for them because they like shortcuts, but I tend to shy away from this. What matters is that a student understands how to work with the formal definition, not that he or she can memorize some random facts that may or may not apply in a given setting. (Memorization can be especially problematic if a student remembers a random fact incorrectly, or thinks that if he/she can’t remember a random fact, he/she can’t answer a particular question.) If a student starts noticing such a pattern on his or her own, then by all means, a tutor should help him or her understand why such patterns emerge. The same goes for students whose instructors do reveal the patterns to them. While I don’t agree with those instructors, it’s their right to present the material in the best way they see fit!
The issue of whether to present some general fact or property to students is a precarious one for instructors as well as for tutors. There is certainly no agreement on which facts are random and which are fundamental! As educators, we should all be encouraging students to pursue a deep understanding of the topics they encounter. Tutors must use their best judgement when they encounter such issues in the ALC. (This could be a very interesting topic to discuss at a future meeting!)



Leave a Reply