Numerical Methods Calculators can be built in any programming language or other tool capable of basic computation. The following examples all compute the answer to this exercise (also covered in class):
Exercise. Given the initial value problem $y’ = 3 – 2x – 0.5y, y(0)=1$, approximate the value of $y(1)$ using Euler’s Method with 10 intervals.
Contents
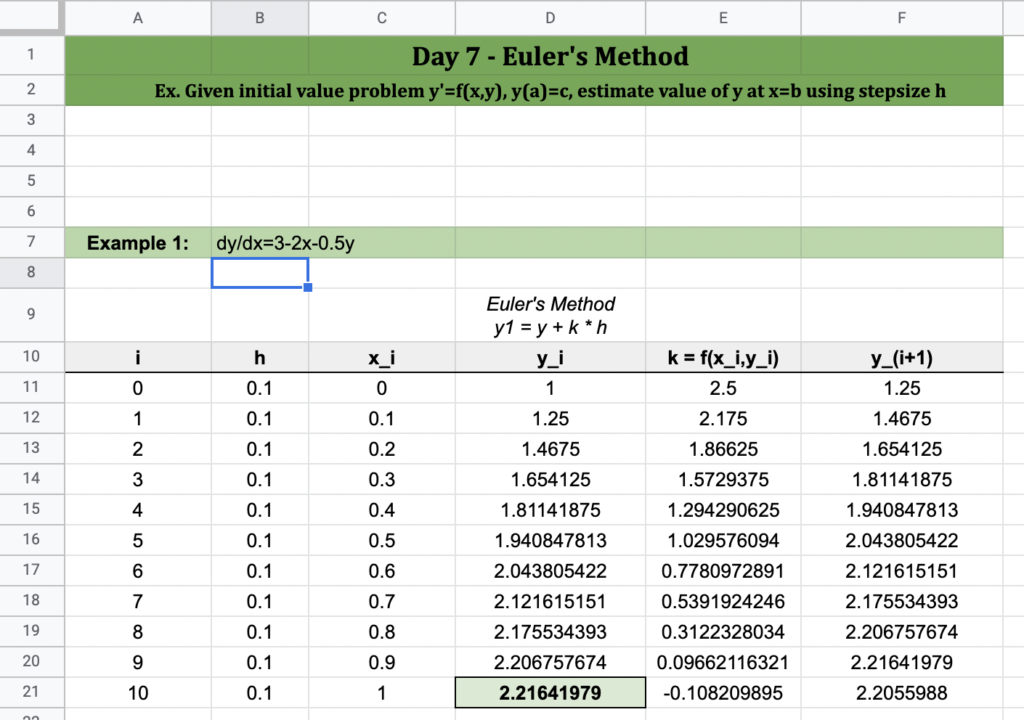
Example 1 – Euler’s Method in a spreadsheet
Here is an image of a numerical methods calculator created in a spreadsheet (Google Sheets). Note that only the first row of data is entered by hand – subsequent values are calculated using formulas.
Example 2 – Euler’s Method in scratch
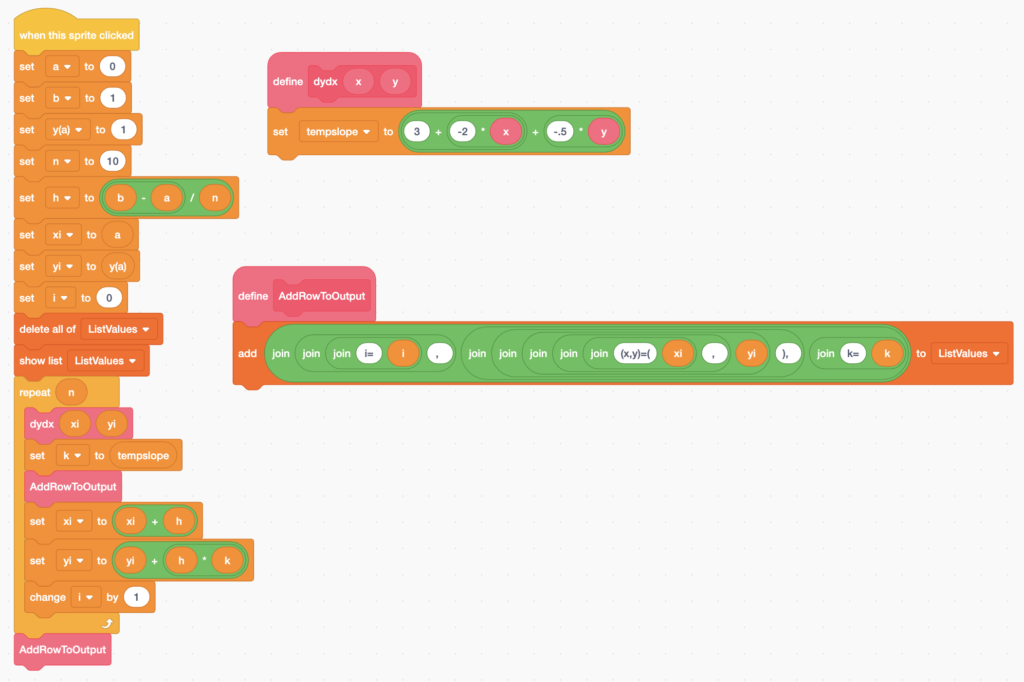
Here is an example created in scratch, MIT’s visual drag-and-drop platform for teaching code. Scratch has a lot of fun features that have to do with animating and interacting with sprites, but the focus of this project is just on the calculation. A list is used to display each row of the output.
Here is the project code:
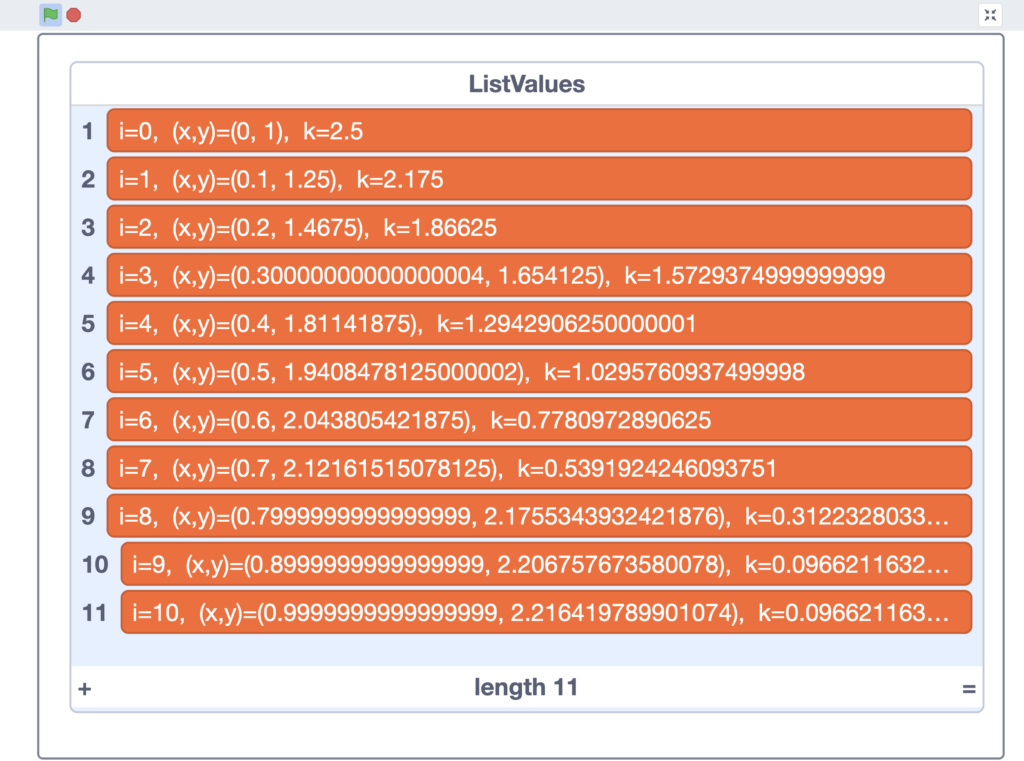
And here is the final output when the scratch project is run:
Example 3 – Euler’s Method in Rockstar
Rockstar is a quirky programming language designed to make your code look like rock lyrics. The following code solves the example given at the top of the page, but with n=30 intervals (instead of 10).
You can run the code by copy/pasting it into the rockstar website and clicking “Rock”.
My brain is overcooked.
My soul is abbreviated.
Your complaint is animalistic.
My pain is not alleviated.
Let my passion be your complaint without my brain.
Let my passion be over my pain.
Let a brain be my brain.
Let a soul be my soul.
The moment is nothing.
Misery takes Brain and Soul
Give 3 - 2*Brain - 0.5*Soul
While the moment is as little as my pain
Shout "i=" with the moment, " (x,y)=(", a brain, ", ", a soul, ") k=", Misery taking a brain, a soul
Let a soul be with my passion of Misery taking a brain, a soul
Let a brain be with my passion
Build the moment upAnd here is the final output when the Rockstar code is run:
i=null (x,y)=(0, 1) k=2.5
i=1 (x,y)=(0.03333333333333333, 1.0833333333333333) k=2.3916666666666666
i=2 (x,y)=(0.06666666666666667, 1.1630555555555555) k=2.285138888888889
i=3 (x,y)=(0.1, 1.2392268518518519) k=2.180386574074074
i=4 (x,y)=(0.13333333333333333, 1.3119064043209876) k=2.0773801311728395
i=5 (x,y)=(0.16666666666666666, 1.3811524086934155) k=1.9760904623199589
i=6 (x,y)=(0.19999999999999998, 1.4470220907707474) k=1.8764889546146264
i=7 (x,y)=(0.2333333333333333, 1.5095717225912348) k=1.7785474720377157
i=8 (x,y)=(0.26666666666666666, 1.5688566383258253) k=1.6822383475037541
i=9 (x,y)=(0.3, 1.6249312499092838) k=1.587534375045358
i=10 (x,y)=(0.3333333333333333, 1.6778490624107958) k=1.4944088021279356
i=11 (x,y)=(0.36666666666666664, 1.7276626891483937) k=1.4028353220924696
i=12 (x,y)=(0.39999999999999997, 1.774423866551476) k=1.3127880667242622
i=13 (x,y)=(0.4333333333333333, 1.818183468775618) k=1.2242415989455244
i=14 (x,y)=(0.4666666666666666, 1.858991522073802) k=1.1371709056297659
i=15 (x,y)=(0.49999999999999994, 1.8968972189281275) k=1.0515513905359364
i=16 (x,y)=(0.5333333333333333, 1.931948931945992) k=0.9673588673603374
i=17 (x,y)=(0.5666666666666667, 1.9641942275246698) k=0.8845695529043318
i=18 (x,y)=(0.6, 1.9936798792881474) k=0.8031600603559264
i=19 (x,y)=(0.6333333333333333, 2.0204518813000116) k=0.7231073926833276
i=20 (x,y)=(0.6666666666666666, 2.0445554610561225) k=0.6443889361386055
i=21 (x,y)=(0.7, 2.066035092260743) k=0.5669824538696286
i=22 (x,y)=(0.7333333333333333, 2.0849345073897303) k=0.4908660796384683
i=23 (x,y)=(0.7666666666666666, 2.101296710044346) k=0.41601831164449377
i=24 (x,y)=(0.7999999999999999, 2.1151639870991623) k=0.342418006450419
i=25 (x,y)=(0.8333333333333333, 2.1265779206475095) k=0.27004437300957873
i=26 (x,y)=(0.8666666666666666, 2.135579399747829) k=0.19887696679275235
i=27 (x,y)=(0.8999999999999999, 2.142208631974254) k=0.1288956840128732
i=28 (x,y)=(0.9333333333333332, 2.146505154774683) k=0.06008075594599194
i=29 (x,y)=(0.9666666666666666, 2.1485078466395495) k=-0.007587256653107888
i=30 (x,y)=(0.9999999999999999, 2.148254938084446) k=-0.07412746904222267
Program completed in 133 ms



Leave a Reply