Worked example of the applications of trig equations

Posted on May 16, 2017 by Sybil Shaver

This is one of the problems which are given in the Test 4 review. Please do not try to just memorize the words I have used here. Make sure that you understand what you are doing at each stage and that you can say it clearly (and using correct vocabulary when it is called for).

 

Solve the equation for t in the first cycle, as we did in the Application in class: show all work, including use of the unit circle, and explain in words what you are doing at each step.

0 = 6\sin(40\pi t)

I will first substitute x in place of the input $\latex 40\pi t$ to simplify the equation:

0 = 6\sin(x)

Next I solve this equation for \sin(x):

\frac{0}{6} = \frac{6\sin(x)}{6}

0 = \sin(x) or \sin(x) = 0

I solve this equation for all the solutions x in [0, 2\pi):

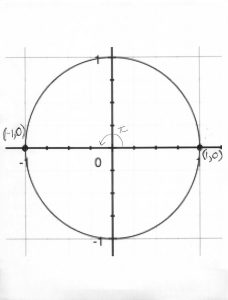
Since the sine is the second coordinate,  find points on the unit circle whose second coordinate is 0. There are two points: (1, 0) and (-1, 0), shown on my unit circle.

For the point (1, 0), the angle is 0.

For the point (-1, 0), the angle is  \pi.

So I have two solutions, x=0 or x=\pi.

I will now find the values of t by substituting back x=40\pi t:

In the first solution, 40\pi t=0 so t=0. (Zero product property.)

In the second solution, 40\pi t=\pi

\frac{40\pi t}{40\pi}=\frac{\pi}{40\pi} t=\frac{1}{40}

So there are two solutions in the first cycle:  t=0 or t=\frac{1}{40}.

 

This entry was posted in Uncategorized. Bookmark the permalink.