Integration – Partial Fraction Decomposition (cont.)

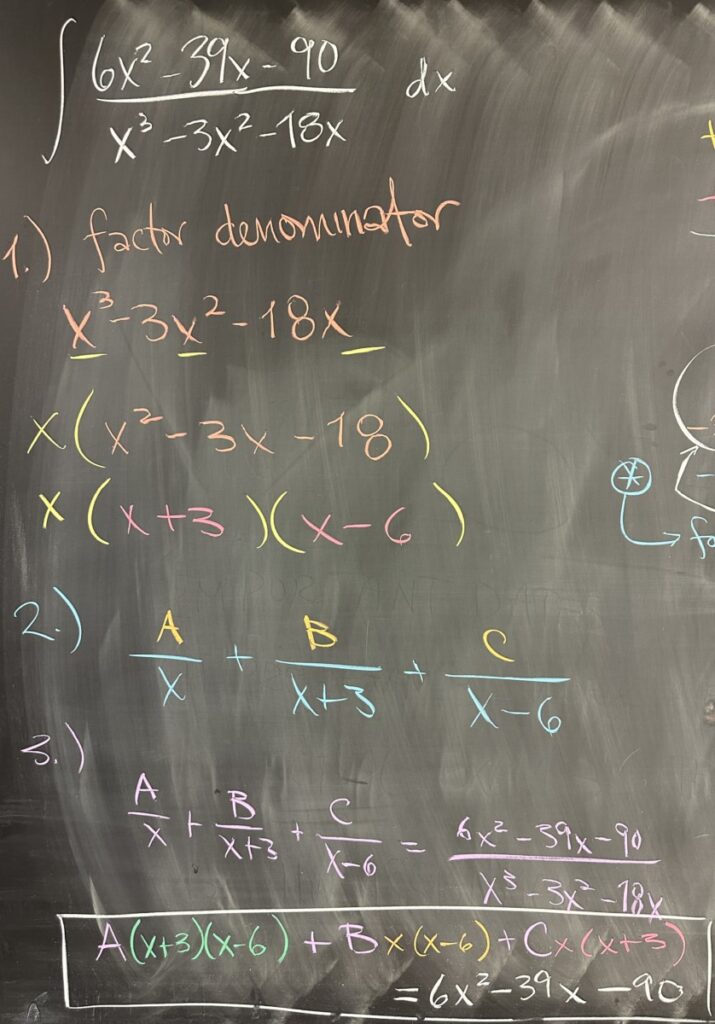
Today’s quiz consisted of a single indefinite integral with several guiding questions on navigating the process of Partial Fraction Decomposition.

Our first task is to factor the denominator: \[x^3-3x^2-18x = x(x+3)(x-6)\]

Then, each unique factor gets its own fraction: \[\frac{A}{x}+\frac{B}{x+3}+\frac{C}{x-6}\]

Once we have the form for the decomposition, we set our form equal to the original fraction that we want to decompose: \[\frac{A}{x}+\frac{B}{x+3}+\frac{C}{x-6}=\frac{6x^2-39x-90}{x^3-3x^2-18x}\]

From this there are multiple methods to reduce this down to a polynomial equation (multiply both sides by the common denominator, or manipulate each fraction until the common denominator is held by all fractions in the equation):\[A(x+3)(x-6) + Bx(x-6) + Cx(x+3) = 6x^2-39x-90\]

After using the distributive property on all products, we can see how the like terms must combine. Remember that this equation must hold for ALL values of \(x\) and we aim to find the values for \(A\), \(B\), and \(C\).

For the \(x^2\) terms, the left side coefficients form \(A + B + C\), which must match the coefficient of \(6\) on the right side.

For the \(x\) terms, the left side coefficients form \(-3A-6B+3C\), which must match the coefficient of \(-24\) on the right.

And finally, there is only one constant term on each side, so they must be equal: \(-18A = -90\), which requires that \(A = 5\).

Once we know that \(A = 5\), the other two equations swap out \(A\) for \(5\), leaving two equations with two unknowns (\(B\) and \(C\)): \(B + C = 1\) and \(-6B + 3C = -24\).

Either substitution or elimination methods may be used here to conclude that \(C = -2\) and \(B = 3\).

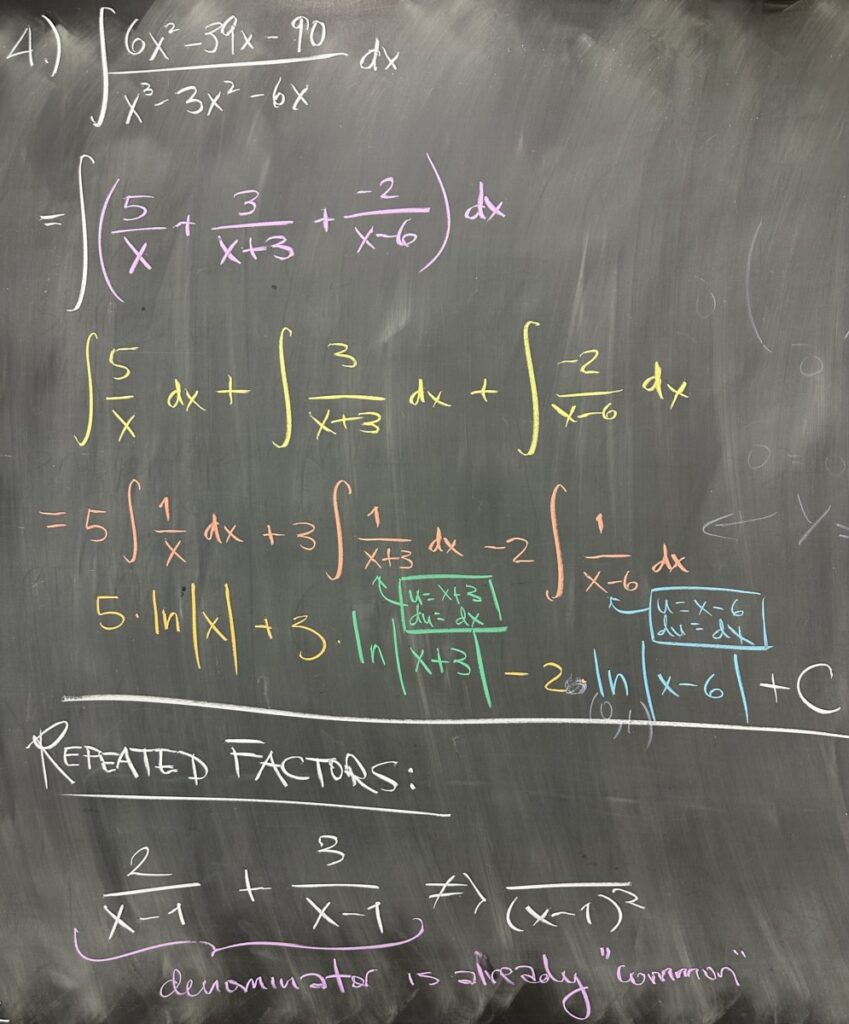
Finally, once the values for \(A\), \(B\), and \(C\) are determined, we can return to the original task of integrating our original fraction. In its decomposed form, the fraction is more straightforward to integrate: \[\int \frac{5}{x} \, dx + \int \frac{3}{x+3} \, dx + \int \frac{-2}{x-6} \, dx\]

The first integral requires no additional techniques, since the antiderivative of \(\frac{1}{x}\) is \(\ln|x|\). The remaining two integrals have similar antiderivative, but require a quick substitution: \(u = x+3\) in the second integral, and \(u = x-6\) in the third. \[5\ln|x| +3\ln|x+3| – 2\ln|x-6| + C\]

After the quiz, it was time to continue looking at more possibilities for denominator factors. First, what happens if we see a factor repeated? For example \((x-1)^2\) (in other terms \((x-1)(x-1)\)). It does not make sense to give “each factor” its own fraction, since there are two copies of the same factor. If we create two fractions with the same factor in the denominator, they can already combine and we are being redundant.

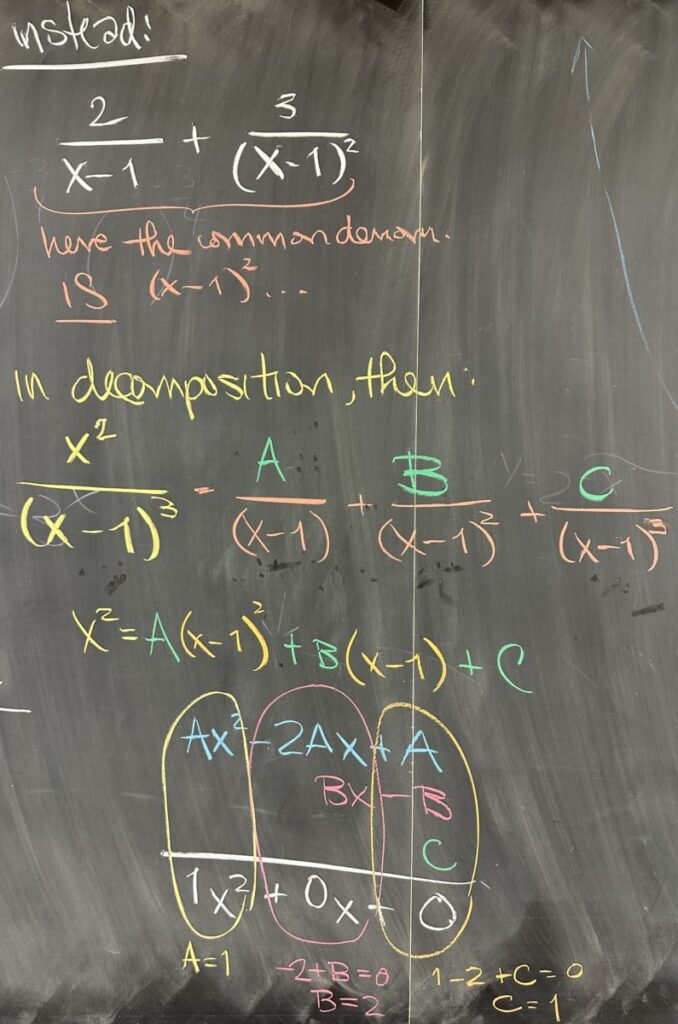
Instead, we still look at two fractions, but one with denominator \(x-1\) and the second with denominator \((x-1)^2\). In fact, whenever we see repeated factors, we will take the same approach. For example: \[\frac{x^2}{(x-1)^3} = \frac{A}{x-1} + \frac{B}{(x-1)^3} + \frac{C}{(x-1)^3} \]

In this way, we cover all possible degrees for a “proper” fraction with denominator \((x-1)^3\).

Working this one out (similar to the quiz problem) we reduce the equation to \[x^2 = A(x-1)^2 + B(x-1) + C\]

After lining up our like terms to create separate equations in \(A\), \(B\), and \(C\), we quickly find that \(A = 1\) and from that we conclude that \(B = 2\) and \(C =1\).

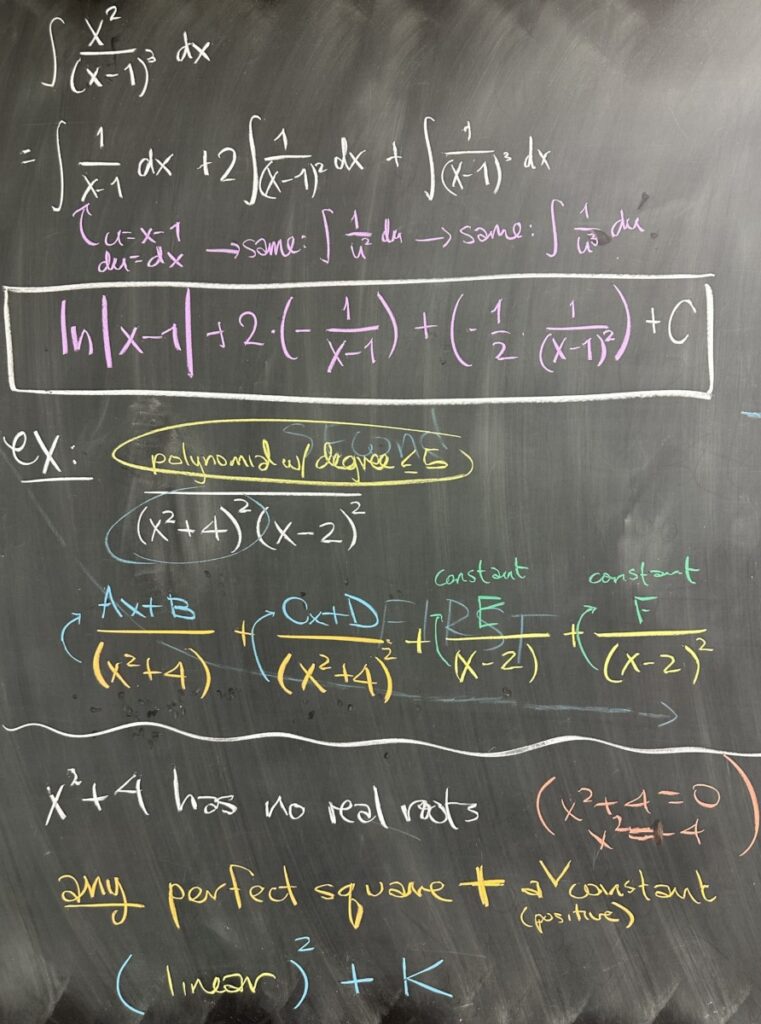
If we then try to integrate our original fraction, we again can replace the fraction with its decomposition: \[\int \frac{1}{x-1}\,dx + 2\int \frac{1}{(x-1)^2}\,dx + \int \frac{1}{(x-1)^3}\,dx\]

Each of these can be substituted with \(u = x-1\) (and \(du = dx\)): \[\int \frac{1}{u}\,du + 2\int \frac{1}{u^2}\,du + \int \frac{1}{u^3}\,du\]

The first integral is a natural logarithm, and the remaining two are power rule integrals: \[\ln|x-1| – \frac{2}{u} – \frac{1}{2u^2} + C\]

In the case of repeated quadratic factors, we have the same tactic: one fraction for each increasing repetition of the factor — and in each numerator we use the pattern dictated by the denominator: linear numerators when the denominator is quadratic, and constant numerators when the denominator is linear. \[\frac{x^5}{(x^2+4)^2(x-2)^2} = \frac{Ax + B}{x^2+4} + \frac{Cx + D}{(x^2+4)^2} + \frac{E}{x-2} + \frac{F}{(x-2)^2}\]

Recall that a quadratic factor is “irreducible” (cannot be factored further) whenever we have a perfect square plus a positive constant. \(x^2 + 4\) is an example of this, as would be \((x+1)^2 + 4\) (in other terms \(x^2 + 2x + 5\).

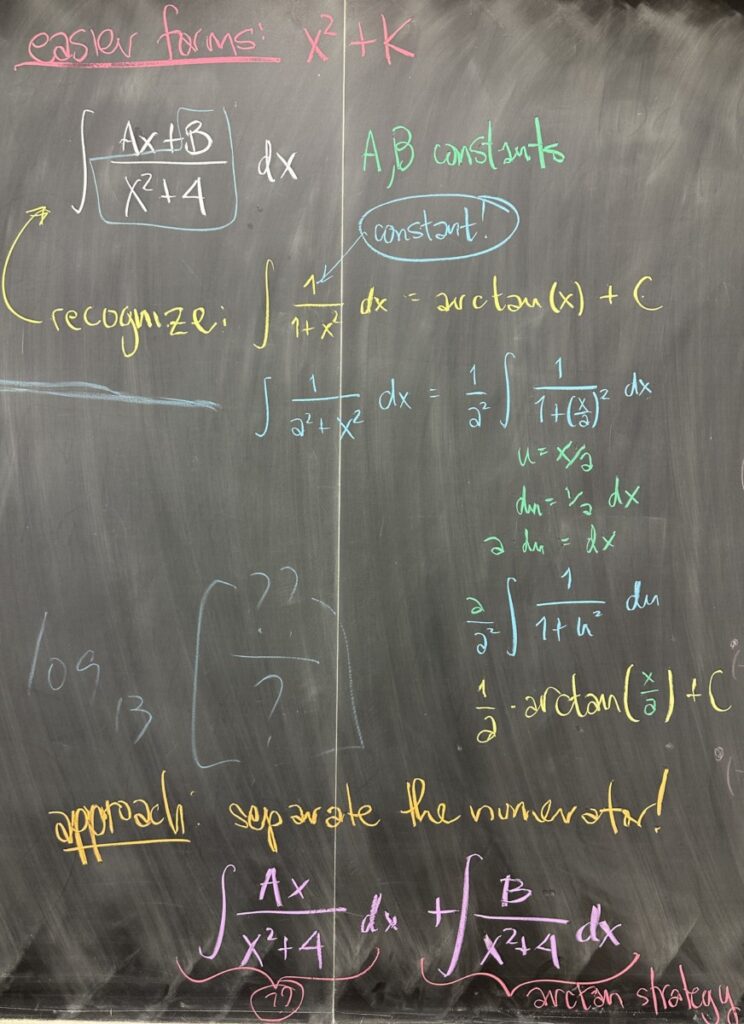
So we know that with linear factors in the denominator, the integration technique will always be u-substitution. But what about quadratic factors in the denominator?

First we recognize that a denominator like \(x^2 + 4\) is reminiscent of integrals that result in arctangent. \[\int\frac{1}{u^2 + a^2}\,du = \frac{1}{a}\arctan\left(\frac{u}{a}\right) + C\]

This is fine for numerators that are constant. But what happens if we have a linear term in the numerator as well? In that case, we split into two distinct integrals: \[\int\frac{Ax+B}{x^2+4}\,dx = A\int\frac{x}{x^2+4}\,dx + B\int\frac{1}{x^2 + 4}\,dx\]

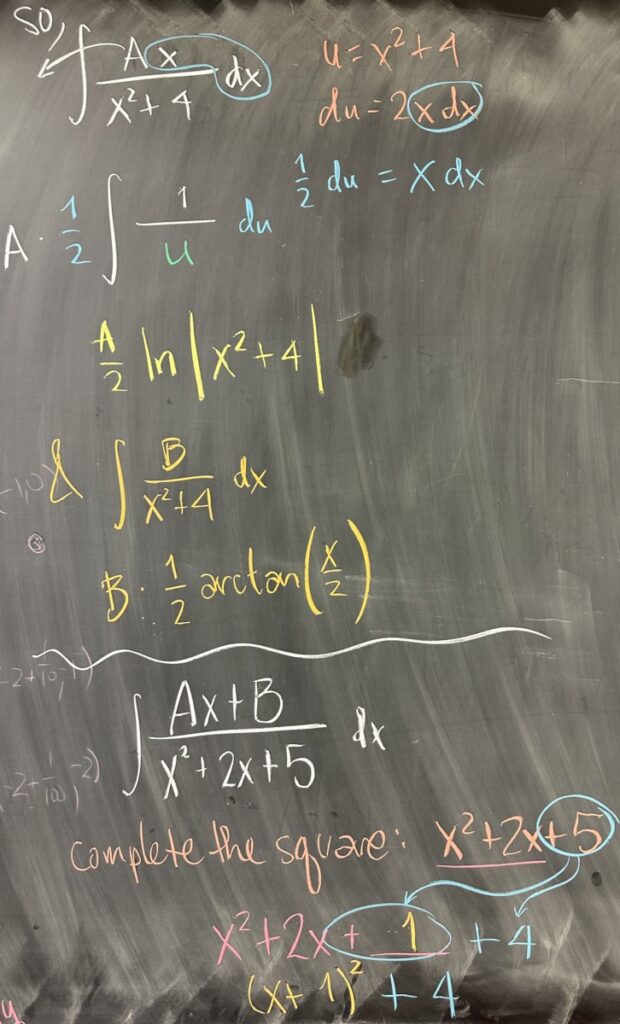
Since we’ve already handled the \(\int\frac{1}{x^2+4}\,dx\) case, we only need to consider \(\int\frac{x}{x^2+4}\,dx\).

This is going to be a u-substitution integral, since \(u = x^2+4\) has \(du = 2x\,dx\), and we have an \(x\) with our \(dx\) to easily substitute \(x\,dx = \frac{1}{2}\,du\).

As a result: \[A\int\frac{x}{x^2+4}\,dx + B\int\frac{1}{x^2 + 4}\,dx = \frac{A}{2}\ln|x^2+4| + \frac{B}{2}\arctan\left(\frac{x}{2}\right) + C\]

It can get trickier, for example in the case where our denominator has a factor of \(x^2 + 2x + 5\). We can tell that this quadratic is irreducible by using the quadratic formula to determine that it has complex roots. Using the technique known as “completing the square” we separate the \(+5\) into \(+1 + 4\) and recognize that \(x^2 + 2x + 1\) is equivalent to \((x+1)^2\).

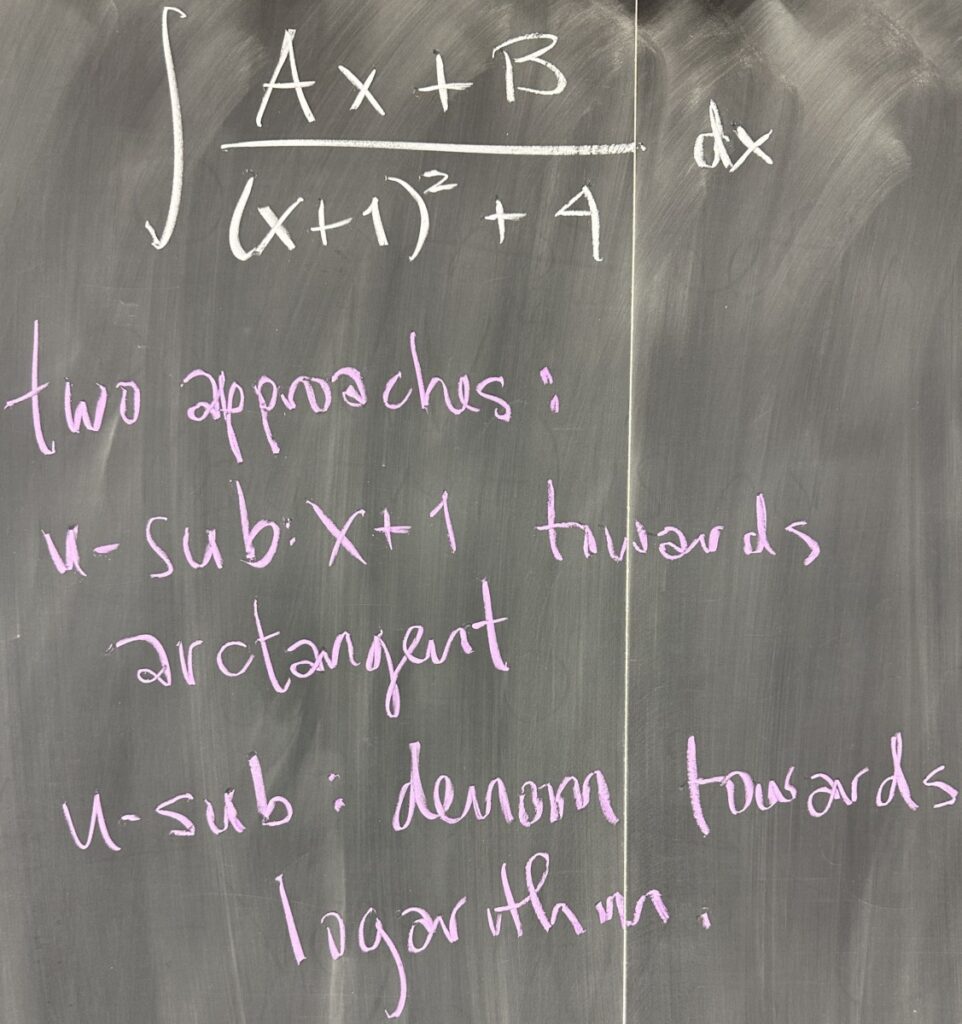
Trying to integrate a decomposition with this denominator is trickier than the last, but still uses the same techniques: separating the linear and constant factors — aiming for arctangent and natural logarithm.