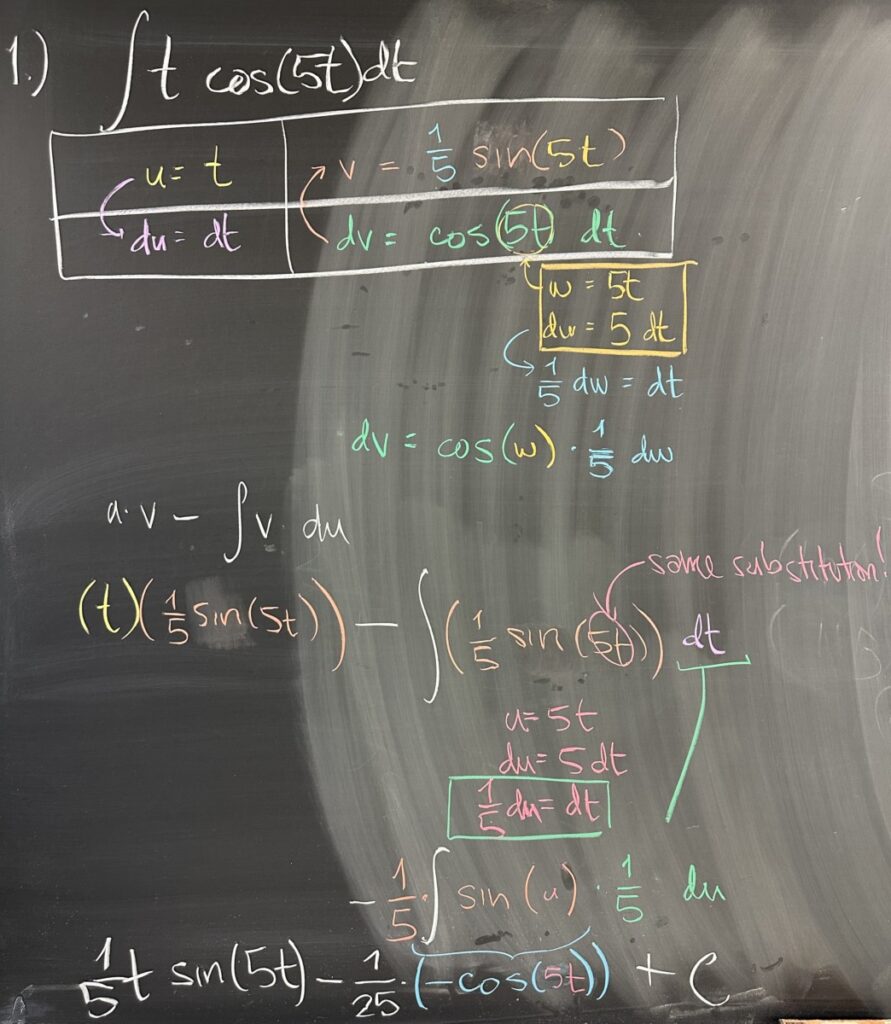
Today’s first quiz problem started with an indefinite integral along with specific choices for \(u\) and \(dv\). With \(u = t\), then \(du\) is the derivative: \(du = 1\,dt\). With \(dv = \cos(5t)\,dt\), then \(v\) is antiderivative: \(v = \int \cos(5t)\,dt\).
However, in order to find \(v\), the antiderivative needs a small substitution: \(w = 5t\) and \(dw = 5\,dt\). Now because \(\int \cos(5t)\, dt\) does not have a factor of \(5 \, dt\), it is convenient to rewrite \(dw = 5\,dt\) as \(\frac{1}{5}\,dw = dt\). Now we can replace \(dt\) with \(\frac{1}{5}\,dw\), and \(\cos(5t)\) with \(\cos(w)\): \[ v = \int \cos(5t)\,dt = \frac{1}{5} \int \cos(w)\,dw = \frac{1}{5} \sin(w) = \frac{1}{5} \sin(5t)\]
This completes the necessary pieces for Integration by Parts: \[uv – \int v\,du = (t)\left(\frac{1}{5}\sin(5t)\right) – \frac{1}{5} \int \sin(5t)\,dt\]
Another substitution (the same substitution, actually) is necessary to complete the remaining antiderivative: \[\frac{1}{5} t \sin(5t) – \frac{1}{25}\left(-\cos(5t)\right) + C\]
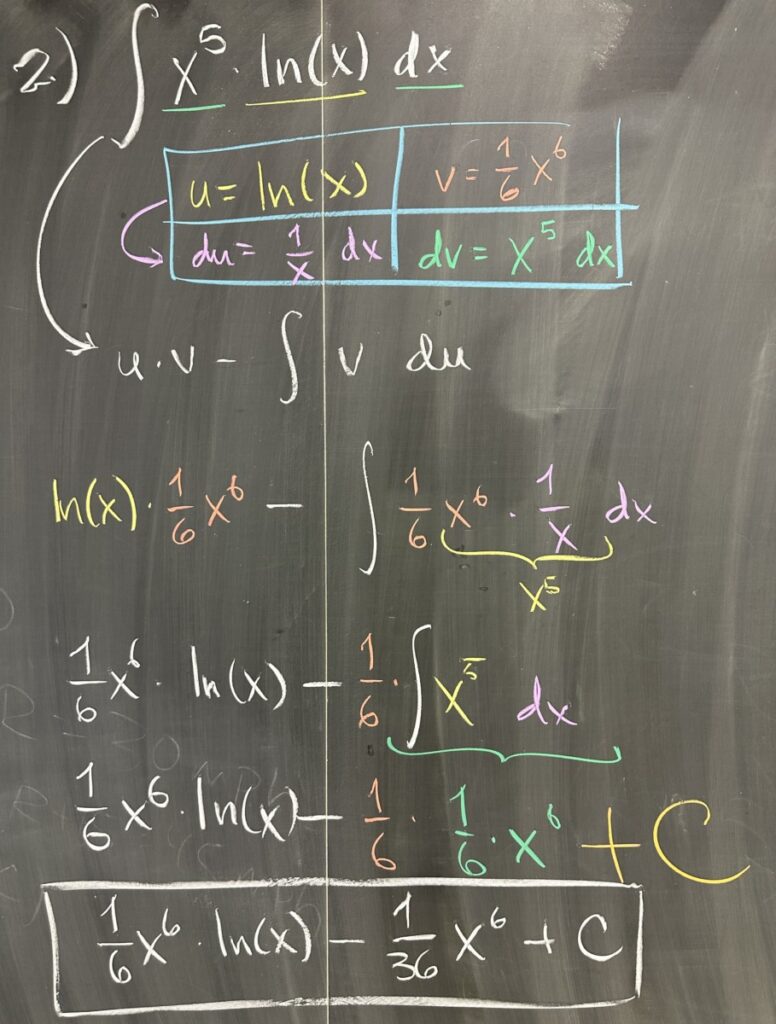
The second quiz problem also required Integration by Parts, but this time, the choice for \(u\) and \(dv\) was left up to you. In this case (and in all cases), \(\ln(x)\) cannot be chosen as \(dv\). This leaves only the option: \(u = \ln(x)\) and \(dv = x^5\,dx\).
The derivative of \(u\) gives us \(du = \frac{1}{x}\,dx\). The antiderivative of \(dv\) gives us \(v = \frac{1}{6}x^6\). Combining all four pieces according to Integration by Parts: \[\frac{1}{6}x^6\ln(x) – \frac{1}{6}\int x^6 \frac{1}{x}\, dx = \frac{1}{6}x^6\ln(x) – \frac{1}{36} x^6 + C\]
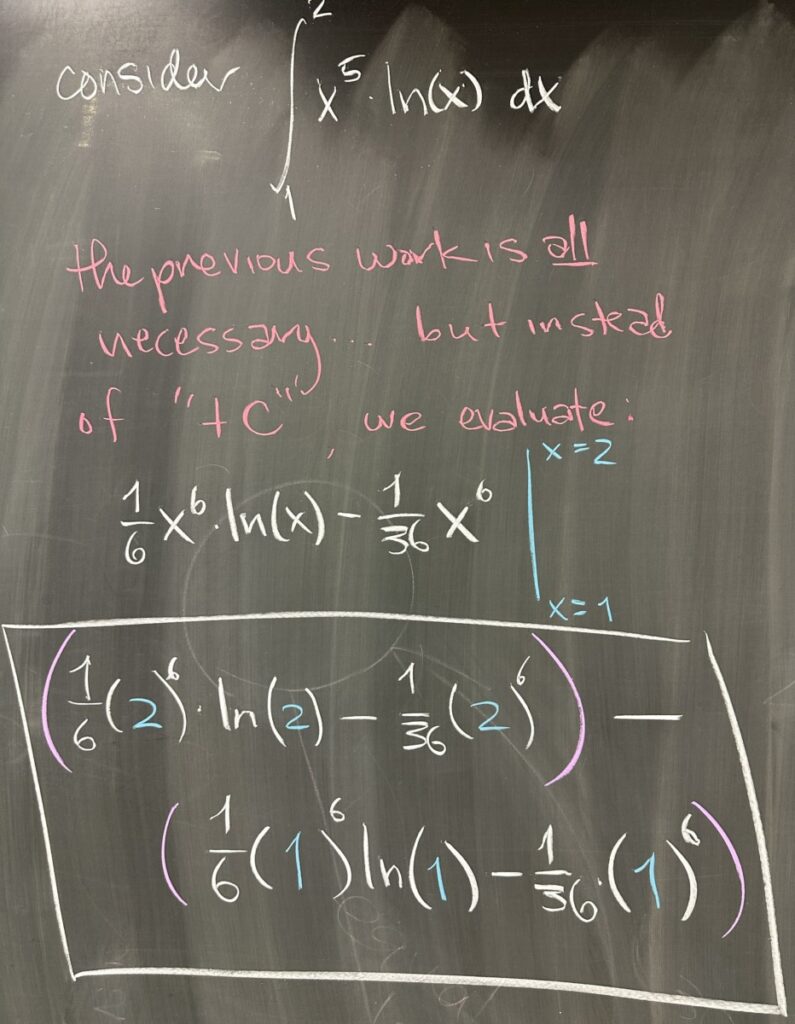
One thing that we have yet to consider is what happens when Integration by Parts is used in the context of a definite integral. Remember that both definite and indefinite integrals require finding an antiderivative. The definite integral then goes a step farther in measuring the difference between the antiderivative’s values at either end of an \([a,b]\) interval.
So, if the second quiz question had been a definite integral, such as: \(\displaystyle \int_{1}^{2} x^5 \ln(x) \, dx\), the additional step of evaluating the antiderivative at \(x=2\) and \(x=1\), then subtracting is necessary.
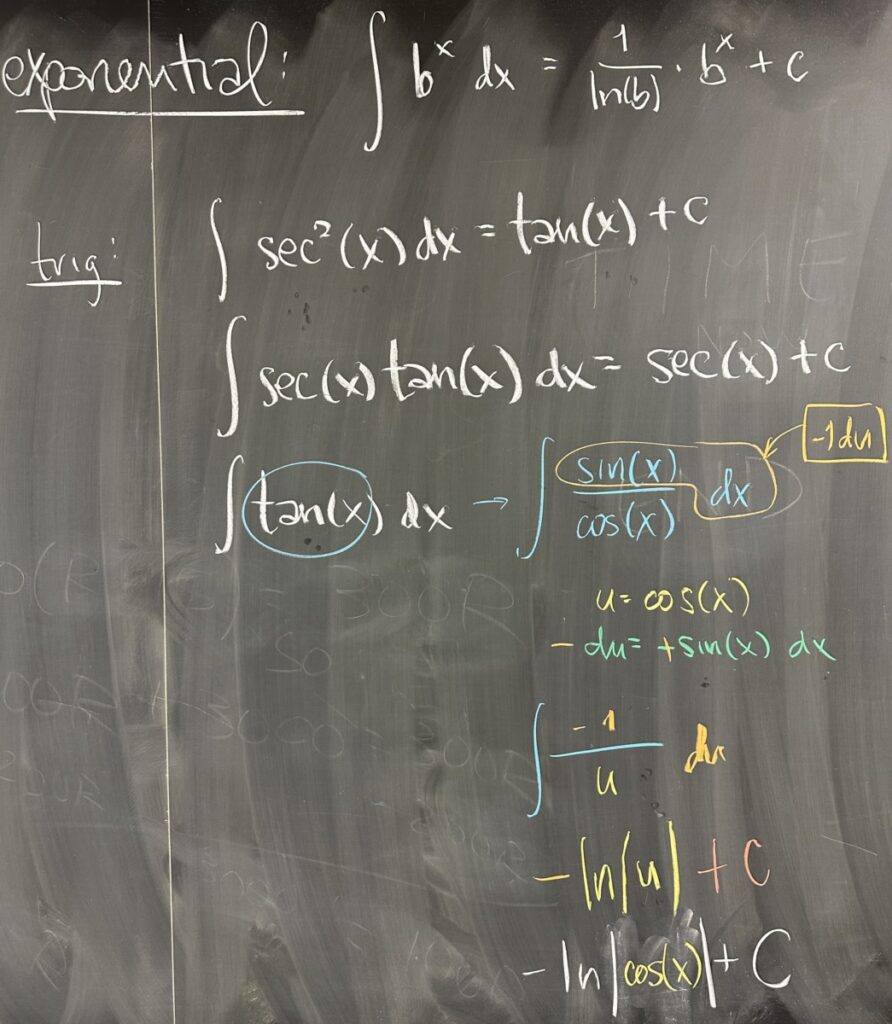
After a quick review of antiderivatives for exponential functions and trigonometric functions, we turn to some trig integrals that are not as clear.
First, because of the pattern that emerges from the derivative of exponential functions: \(\frac{d}{dx}\left[b^x\right] = b^x(\ln b)\), we conclude that the antiderivative is \(\int b^x\,dx = \frac{1}{\ln b} b^x + C\)
Then because \(\frac{d}{dx}\left[\tan(x)\right] = \sec^2(x)\), we conclude that \(\int \sec^2(x)\,dx = \tan(x) + C\).
A similar story is seen with \(\frac{d}{dx}\left[\sec(x)\right] = \sec(x)\tan(x)\), where the antiderivative relationship is \(\int \sec(x)\tan(x)\,dx = \sec(x) + C\).
But when we attempt to identify the antiderivative of \(\tan(x)\), we don’t have a clear answer. Rewriting tangent as the ratio of sine to cosine, we see an opportunity to substitute: \(u = \cos(x)\), with \(du = -\sin(x)\).
\[\int \tan(x)\,dx = \int \frac{\sin(x)}{\cos(x)}\,dx = \int \frac{-1}{u}\,du = -\ln|u| + C = -\ln|\cos(x)| + C\]
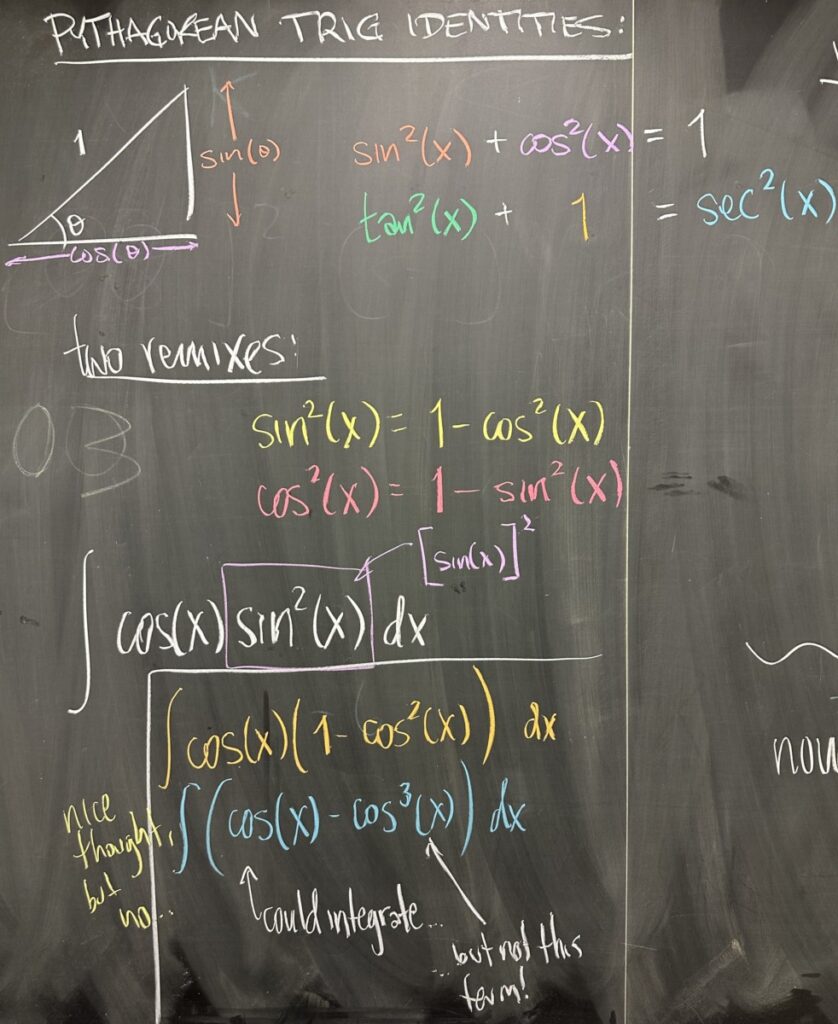
When considering antiderivatives of powers of trigonometric functions, it is often helpful to recall that there are useful relationships between trigonometric functions. The Pythagorean Trig Identities come from the Pythagorean Theorem applied to right triangles seen in the unit circle.
\[\sin^2(x) + \cos^2(x) = 1\]
\[\tan^2(x) + 1 = \sec^2(x)\]
Moving into integrals of powers of sine and cosine, we look at \(\int \cos(x)\sin^2(x)\,dx\). Swapping out \(\sin^2(x)\) leaves us trying to integrate \(\int \cos(x) – \cos^3(x) \, dx\). The first term has a clear antiderivative, but the second term is still hard for us to work with — we wouldn’t be making our task any easier with this exchange of \(\sin^2(x)\).
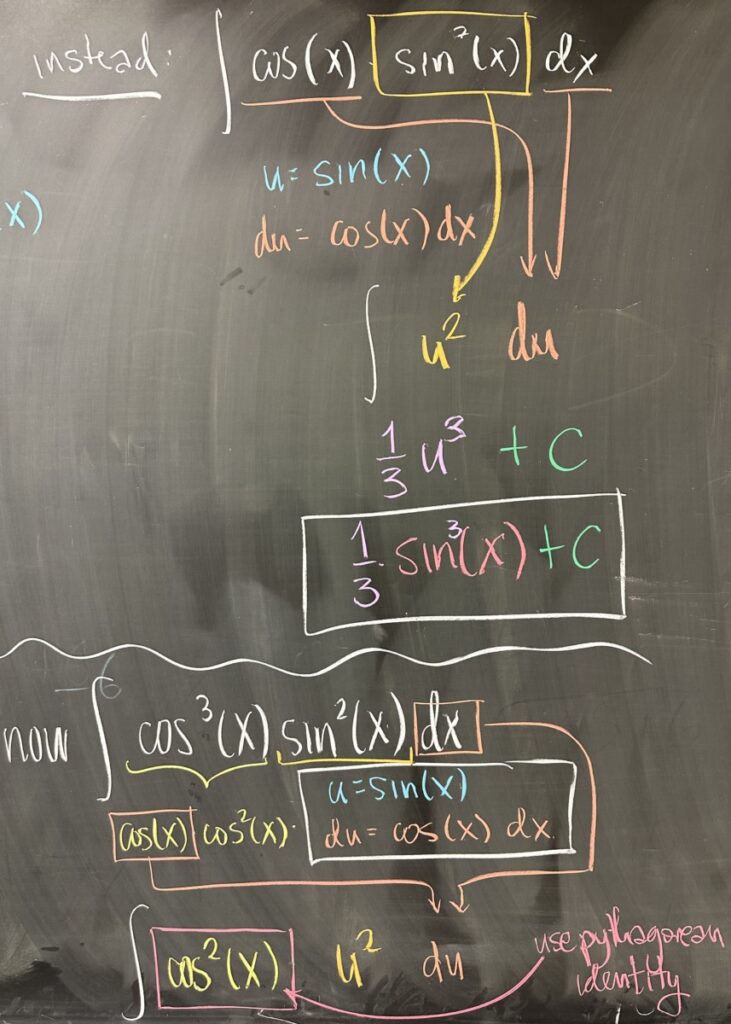
Instead, we recognize that \(\sin^2(x)\) is convenient shorthand for \(\left(\sin(x)\right)^2\), and here we see \(u = \sin(x)\) as a target for substitution. Now \(du = \cos(x)\, dx\), reducing the integral to \[\int u^2 \, du = \frac{1}{3}u^3 + C = \frac{1}{3} \sin^3(x) + C\]
If we look at a similar example, \(\int\cos^3(x)\sin^2(x)\,dx\), the same substitution is still the right move — but not without some additional effort. After substituting \(u = \sin(x)\) and \(du = \cos(x) \, dx\), there is still leftover \(\cos^2(x)\): \[\int\cos^3(x)\sin^2(x)\,dx = \int\cos^2(x)\left(\sin(x)\right)^2\cos(x)\,dx = \int \cos^2(x)u^2\,du\]
Note that there is only one \(dx\) to exchange for \(du\), so what are we supposed to do with the remaining \(\cos^2(x)\)? [Remember: a substitution is only valid if we can exchange all instances of \(x\) and \(dx\) for \(u\) and \(du\).]
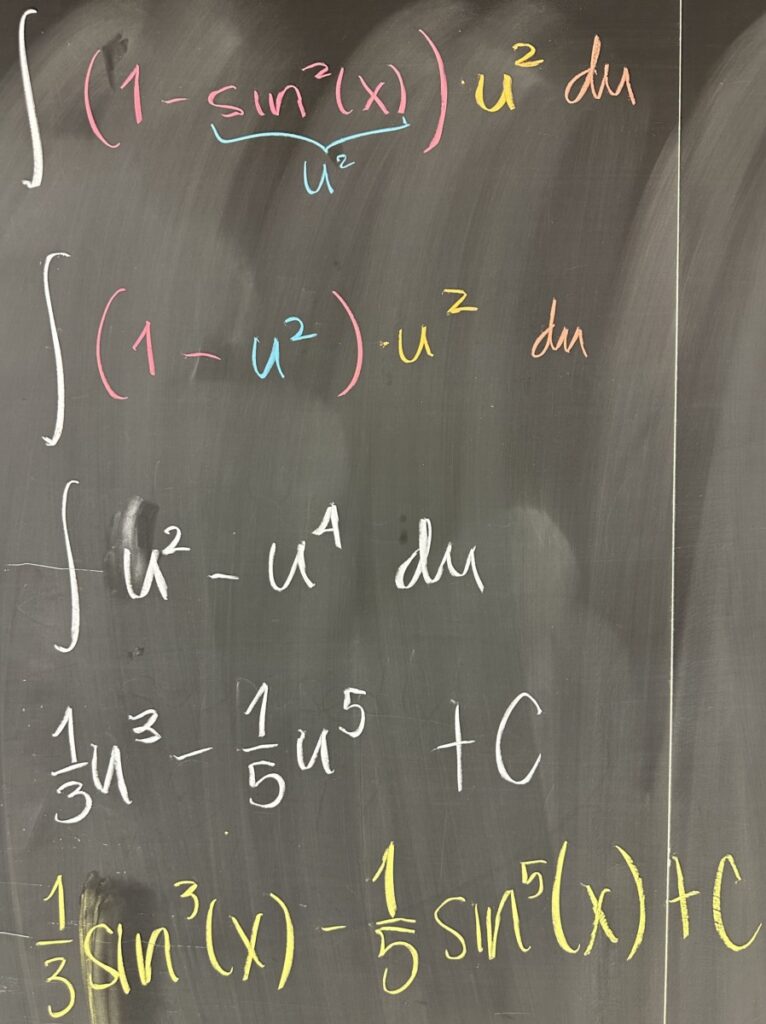
This is a perfect opportunity to use the Pythagorean Trig Identity. We can exchange \(\cos^2(x)\) for \(1 – \sin^2(x)\), which is \(1 – u^2\) with our substitution \(u = \sin(x)\). After this exchange, our substituted integral has finally been fully converted from \(x\) and \(dx\) to \(u\) and \(du\):\[\int (1-u^2)u^2\,du\]
We cannot integrate products, so after using the distributive property we have \[\int u^2 – u^4\,du = \frac{1}{3}u^3 – \frac{1}{5}u^5 + C\]
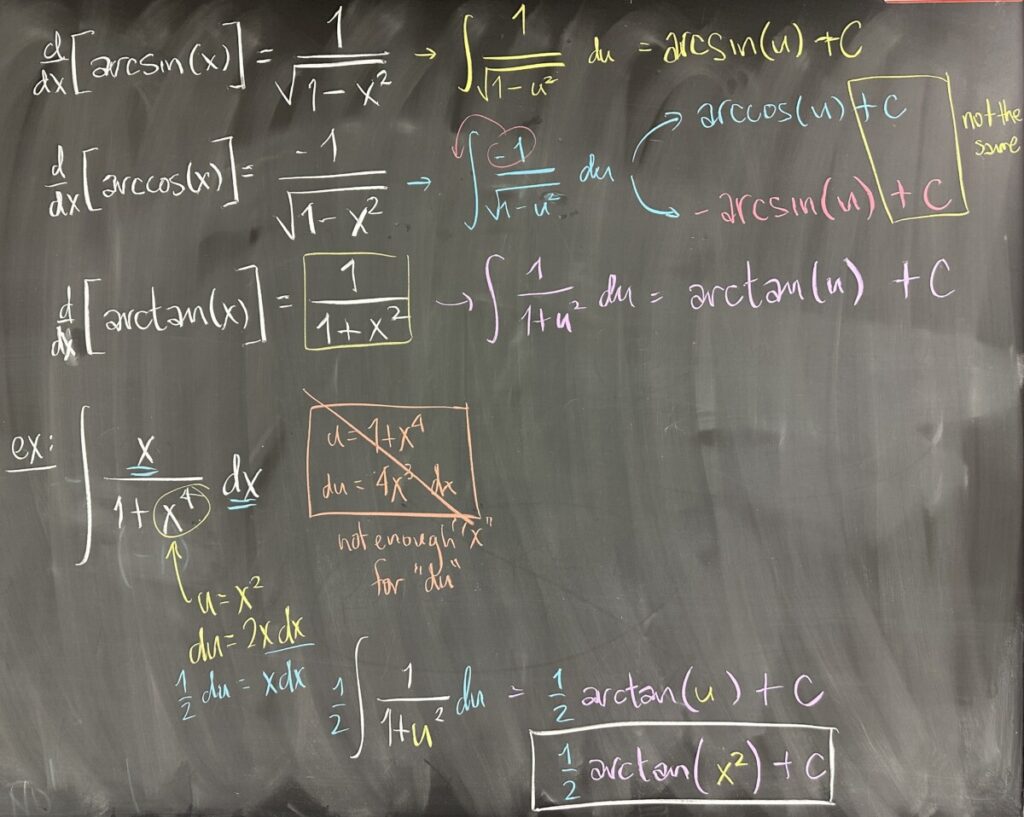
To round out the lesson, we look at the derivatives of the inverse trig functions to identify some ‘easy’ antiderivatives. They don’t look easy, but:
\[\int \frac{1}{\sqrt{1-u^2}}\,du = \arcsin(u) + C\]
\[\int \frac{-1}{\sqrt{1-u^2}}\,du = \arccos(u) + C = -\arcsin(u) + \frac{\pi}{2} + C\]
\[\int \frac{1}{1+u^2}\,du = \arctan(u) + C\]
Then a final example: \(\int \frac{x}{1+x^2}\,dx\)
Sometimes we want to look at the denominator to substitute: \(u = 1+x^4\), with \(du = 4x^3\,dx\); but in this exchange, we need \(x^3\) with \(dx\) and we don’t have it.
Since we know the antiderivative of \(\frac{1}{1+u^2}\), it is actually better to substitute \(u = x^2\), since \(du = 2x\,dx\) (which we actually do have, unlike \(u = 1+x^4\)). So \(\frac{1}{2}\,du = x\,dx\) and then \[\int \frac{x}{1+x^4}\,dx = \frac{1}{2}\int \frac{1}{1+u^2}\,du = \frac{1}{2}\arctan(u) + C = \frac{1}{2}\arctan(x^2)+C\]



Recent Comments