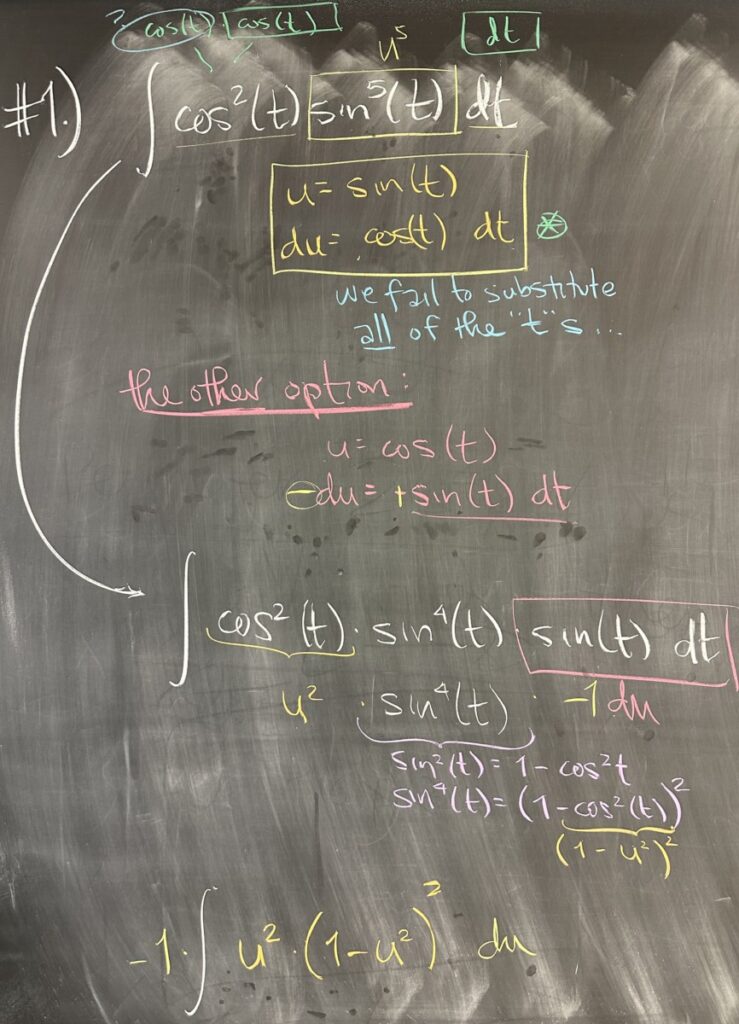
Today’s quiz focused on integrating products of powers of trig functions. In these situations, we see powers of sine and cosine multiplied, or similarly secant and tangent. In our first problem, we have \(\int \cos^2(t)\sin^5(t)\,dt\).
We have two available options for substitution: \(u = \sin(t)\) or \(u = \cos(t)\). Looking first at \(u = \sin(t)\), we recognize that \(du = \cos(t)\,dt\) will leave our substitution incomplete — with a lone \(cos(t)\) that cannot be substituted to \(u\).
On the other hand, with \(u = \cos(t)\), then \(du = -\sin(t)\,dt\) — which will leave us with an even power for sine: \(\cos^2(t)\sin^4(t)\cdot-1\,du\). Remember that the even powers of sine and cosine are interchangeable with the Pythagorean Identity: \[\sin^2(x) + \cos^2(x) = 1\]
In this case, we’ll think of \(\sin^4(t)\) as \(\left(\sin^2(t)\right)^2\). Then we can use the Pythagorean identity to replace \(\sin^2(t) = 1 – \cos^2(t)\), so \(\left(\sin^2(t)\right)^2 = \left(1 – \cos^2(t)\right)^2\). Then because \(u = \cos(t)\), we can convert \(\cos^2(t) = u^2\) and \(\left(1 – \cos^2(t)\right)^2 = (1 – u^2)^2\).
Our integral is now: \[\int \cos^2(t)\sin^5(t)\,dt = \int \cos^2(t)\sin^4(t)\cdot-1\,du = -\int u^2(1-u^2)^2\,du\]
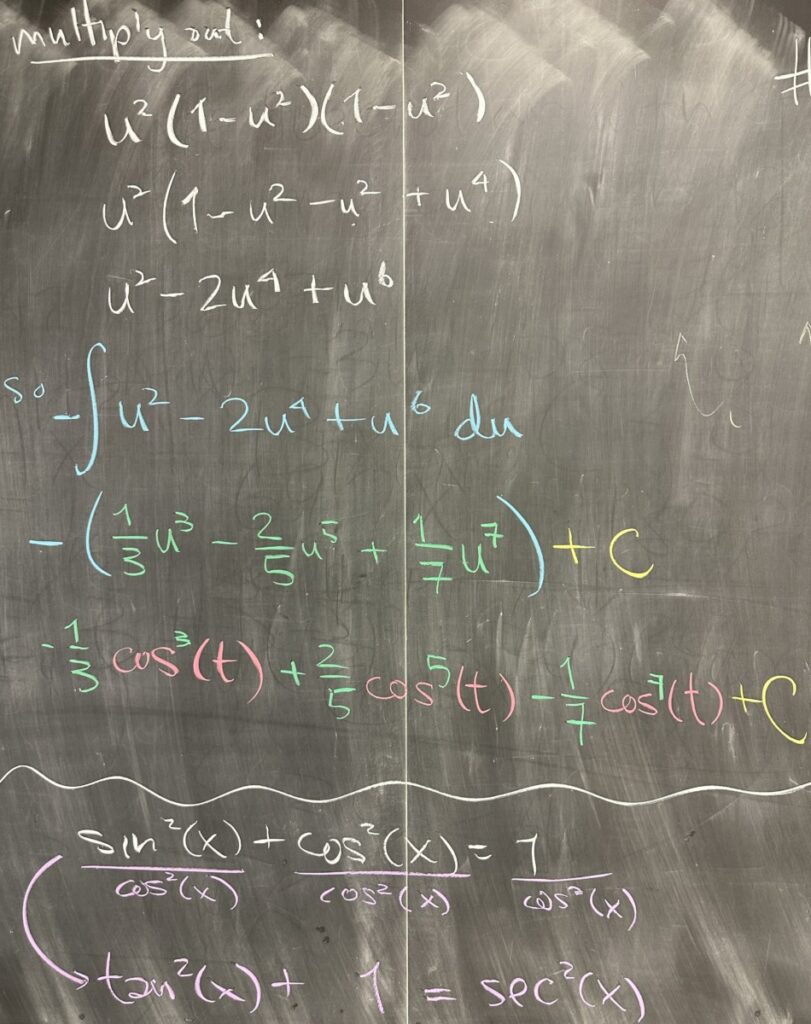
In order to find an antiderivative for \(u^2(1-u^2)^2\) we must first handle the multiplication (otherwise, we’re trying to integrate a product, and that is harder to do than multiplying and integrating the result). After multiplying we have \(u^2 – 2u^4 + u^6\), which can be integrated with just the power rule.
After integrating, we must convert our answer back to the original variable, in this case by re-substituting \(u = \cos(t)\).
I was asked to go over the relationship between the three versions of the Pythagorean Identity. Take the basic version: \[\sin^2(x) + \cos^2(x) = 1\]
Then divide it by either \(\cos^2(x)\): \[\tan^2(x) + 1 = \sec^2(x)\]
Or by \(\sin^2(x)\): \[1 + \cot^2(x) = \csc^2(x)\]

In our second quiz problem, we have paired secant and tangent instead of sines and cosines. Again, we have two easy targets for substitution: \(u = \sec(x)\) or \(u = \tan(x)\).
As we saw in the first problem, the two substitutions often have one that works and one that doesn’t. The trick will be practicing enough problems to ensure that you know the best option. Here, when we consider \(u = \sec(x)\) we get \(du = \sec(x)\tan(x)\,dx\) which would leave us with a lone, un-substitute-able tangent with: \(\int \tan(x)\sec^3(x)\,du\).
So instead we try \(u = \tan(x)\), which has \(du = \sec^2(x)\,dx\). This leaves us with \(\int \tan^2(x)\sec^2(x)\,du\) which isn’t looking too bad — because \(\tan^2(x) = u^2\) and \(\sec^2(x) = \tan^2(x) + 1 = u^2 + 1\).
So our integral becomes: \[\int \tan^2(x)\sec^2(x)\,dx = \int u^2(u^2 + 1)\,du\]
As with problem one, we will have a much easier time integrating if we expand the product: \(u^2(u^2 + 1) = u^4 + u^2\)
Now we finish with the power rule and return to our original variable by replacing \(u = \tan(x)\).
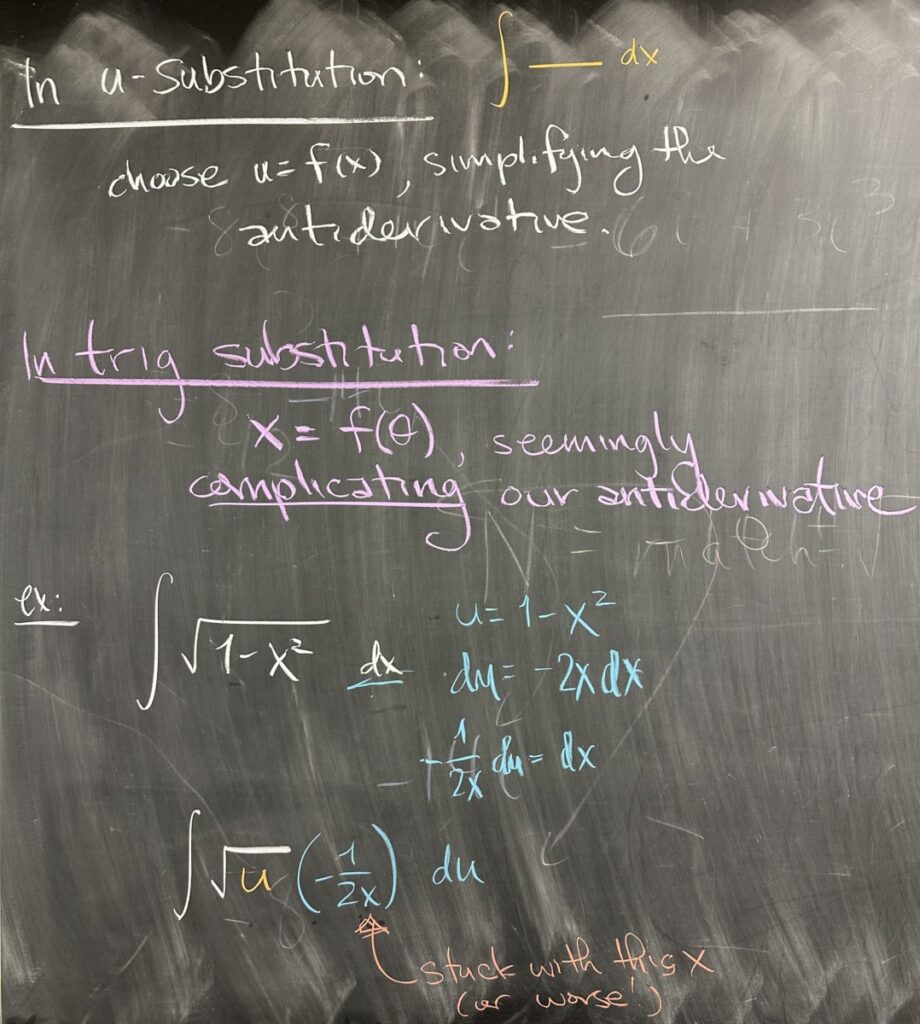
So, with u-Substitution, we are trying to simplify the function whose antiderivative we must find. We take a function of \(x\) and replace it by a \(u\). At the same time, we also convert the differential \(dx\) to \(du\) by using the derivative of our \(u = f(x)\).
On the other hand, we are today going to consider a technique of integration that takes a very different approach. Instead of simplifying our function, we seem to be somehow complicating it. With this new technique, we will be replacing \(x\) with a trigonometric function of a new variable. This technique is called “trigonometric substitution.”
We start by considering a very difficult integral: \(\int \sqrt{1-x^2}\,dx\)
We’ve actually already considered this integral as a definite integral: the area bounded by the upper half of the circle with radius one (centered at the origin). But now we want to find the actual antiderivative, and it will be quite a challenge.
We may initially think of u-Substitution, as we frequently choose \(u\) to be a radicand when we see any radicals in an integral problem. But (it seems to be a theme today), our choice of \(u = 1-x^2\) doesn’t actually work out. This attempt at u-Substitution fails because we cannot resolve the differential: \(du = -2x \, dx\).
We don’t have a factor of \(x\,dx\) to substitute, and if we attempt to do so anyway, we will have an \(x\) that remains and is nearly impossible to convert to \(u\).
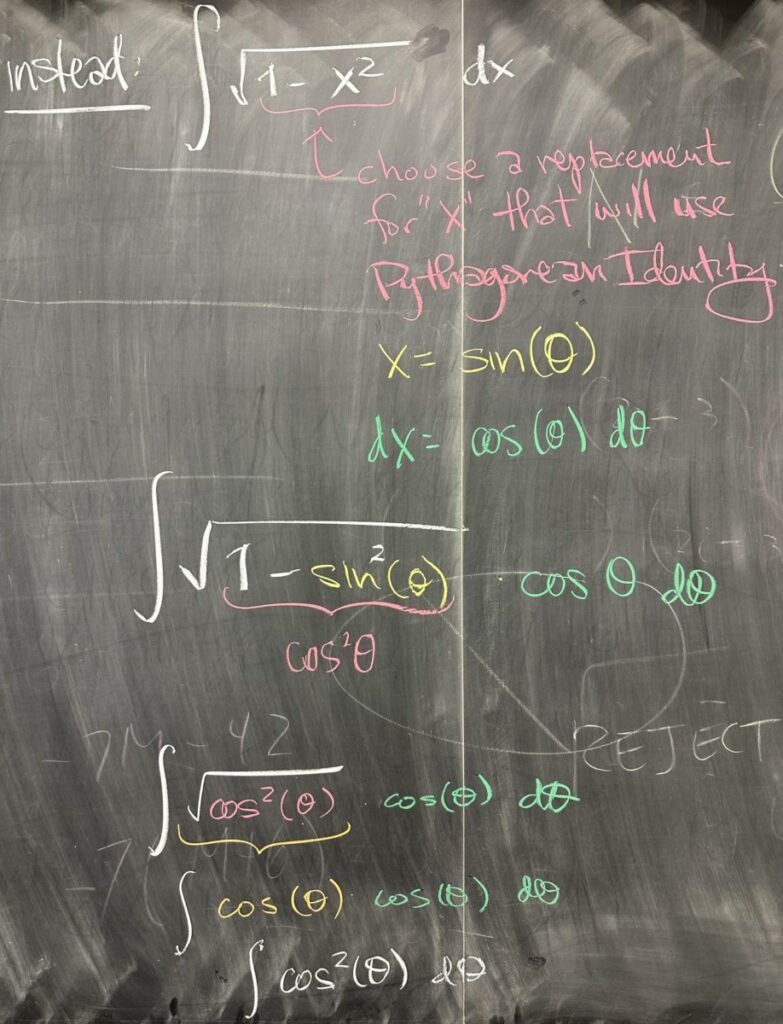
Instead, we will tackle this problem with trig substitution. Replacing \(x = \sin(\theta)\), we get the differential \(dx = \cos(\theta)\,d\theta\), and ultimately the integral looks like: \[\int \sqrt{1 – \sin^2(\theta)}\cdot\cos(\theta)\,d\theta\]
We can use the Pythagorean Identity to convert \(1 – \sin^2(\theta) = \cos^2(\theta)\) and then the square root would be just \(\cos(\theta)\). Combined with the differential \(\cos(\theta)\,d\theta\), we then have: \[\int \cos^2(\theta)\,d\theta\]
This in itself is a difficult integral to compute.
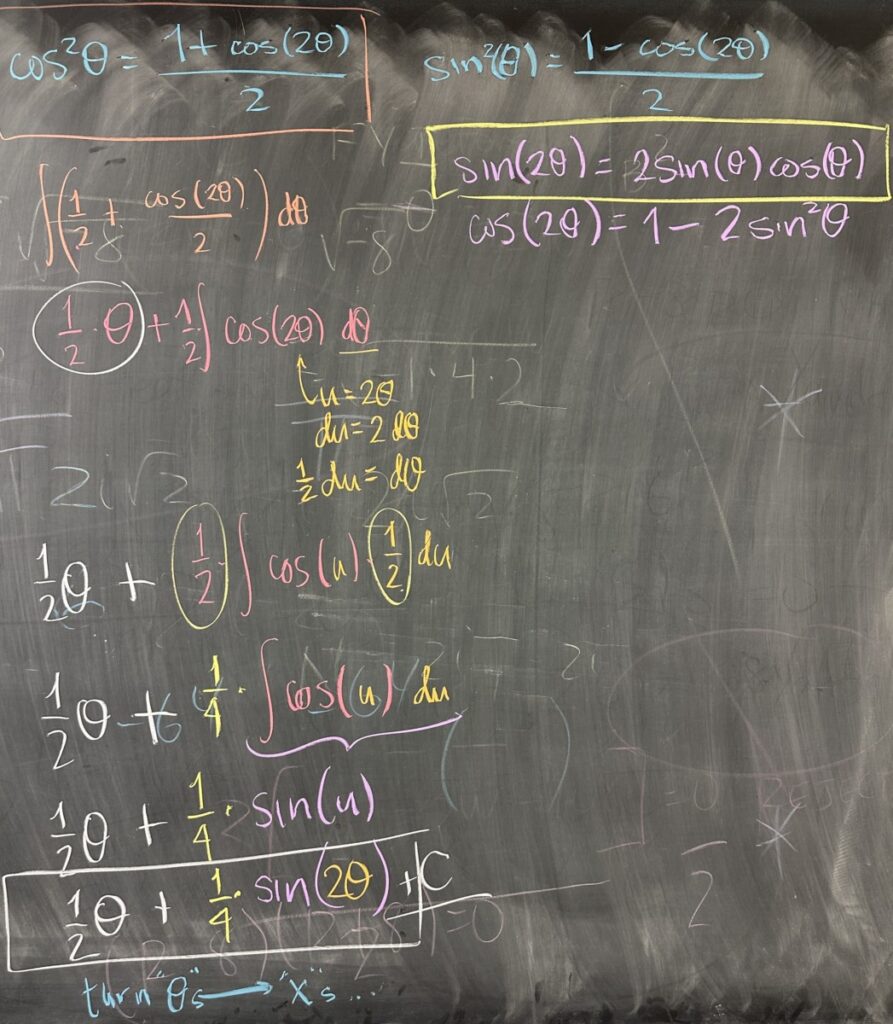
Turning to other trig identities, we see that \(\displaystyle\cos^2(\theta) = \frac{1+\cos(2\theta)}{2}\). This exchange makes our antiderivative easier.
The antiderivative of \(\frac{1}{2}\,d\theta\) is easy, \(\frac{1}{2}\theta\).
The antiderivative of \(\frac{1}{2}\cos(2\theta)\,d\theta\) will require a substitution: \(u = 2\theta\) with \(du = 2 \, d\theta\). So we now want the antiderivative of \(\frac{1}{2}\cos(u)\frac{1}{2}\,du\) — which is \(\frac{1}{4}\sin(u) = \frac{1}{4}\sin(2\theta)\). We know that our final answer is the general antiderivative, so we need a plus C…
…but we’re still not done, unfortunately (what was our original variable?)
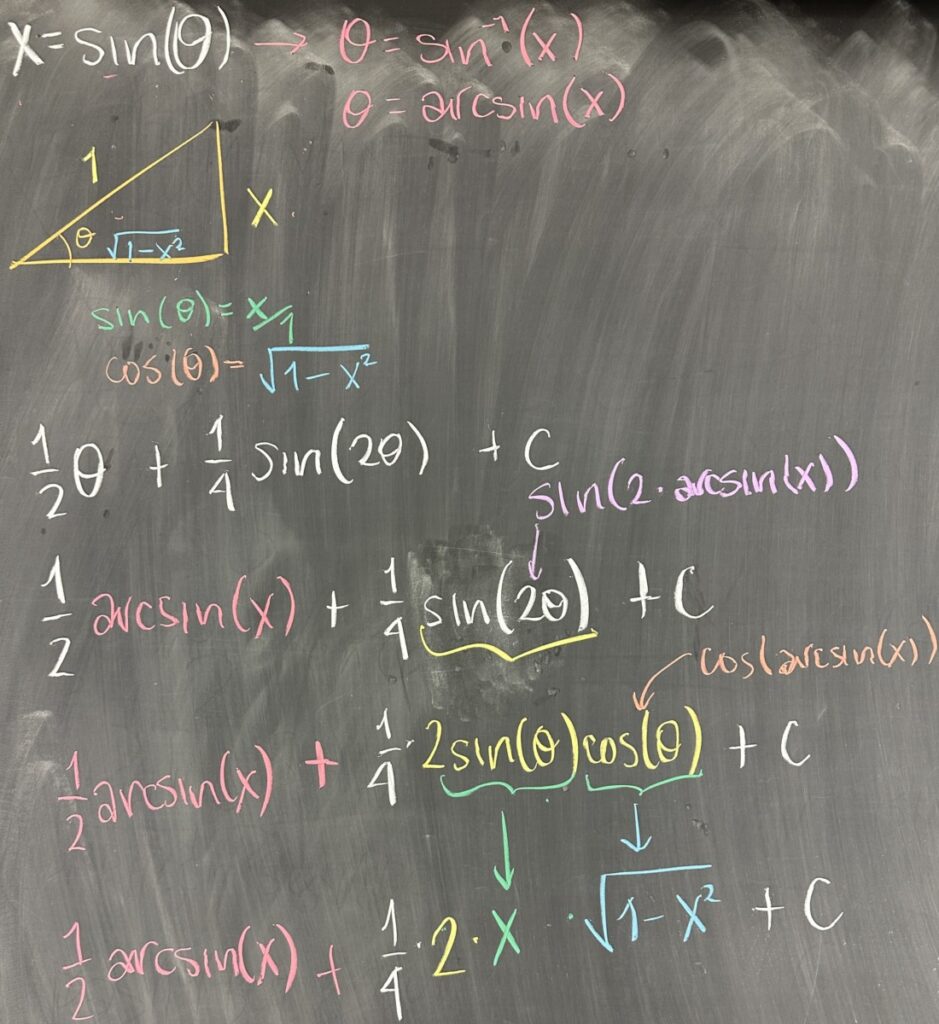
Oh yeah, we originally had \(x\) — for which we substituted \(\sin(\theta)\). Now we have \(\theta\) and we need to get back to \(x\). Well, that relationship is the inverse of the sine: \(\theta = \arcsin(x)\).
I note here that is important to consider the whole picture of the trigonometric functions here. The relationship \(x = \sin(\theta)\) means that the sine ratio of \(\theta\), in other words, the ratio of the leg opposite \(\theta\) to the hypotenuse, is \(x\). We can draw that triangle by making the hypotenuse length \(1\) and the opposite leg to \(\theta\) length \(x\).
Since this picture is one of a right triangle, we know that the Pythagorean Theorem applies and so the remaining leg is the square root of the difference of the squares of the other two sides: \(\sqrt{1^2 – x^2}\). With all three side-lengths known and labeled, we can now substitute: \(\sin(\theta) = x\) (we knew that one already), \(\cos(\theta) = \sqrt{1 – x^2}\), and even \(\tan(\theta) = \frac{x}{\sqrt{1 – x^2}}\).
Here we need to convert \(\frac{1}{2}\theta + \frac{1}{4}\sin(2\theta) + C\).
\(\frac{1}{2}\theta = \frac{1}{2}\arcsin(x)\) is straightforward to convert, but \(\sin(2\theta)\) is not as simple. We again need a trig identity to exchange \(\sin(2\theta) = 2\sin(\theta)\cos(\theta)\). Then we know how to exchange \(\sin(\theta)\) and \(\cos(\theta)\) back to \(x\): \[\frac{1}{4}\sin(2\theta) = \frac{1}{4}2\sin(\theta)\cos(\theta) = \frac{1}{2} x \sqrt{1-x^2}\]
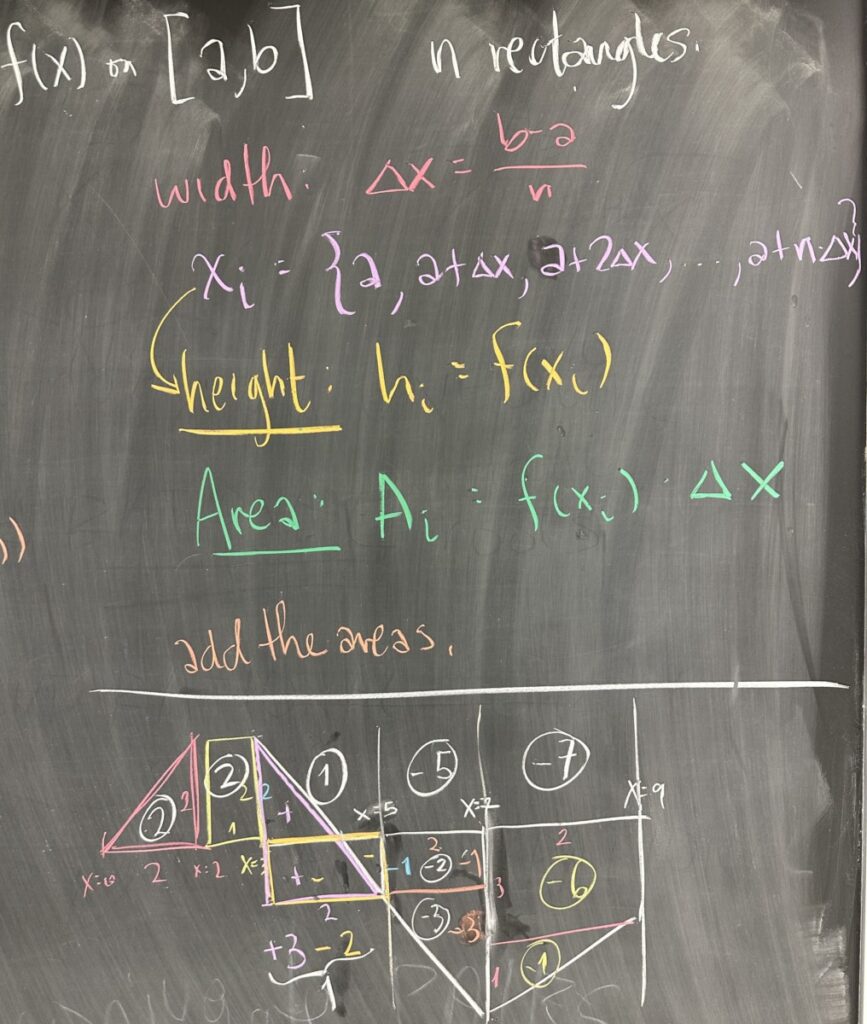
In the last fifteen minutes of class, we discussed a couple of problems from the sample exam. In the first of the two, I covered the general process for computing the Riemann Sum approximation of the area bounded by a function \(y = f(x)\) over an interval from \(x=a\) to \(x=b\), using \(n\) rectangles.
First, split the interval \([a,b]\) into \(n\) pieces and compute the width: \(\Delta x = \frac{b-a}{n}\). Then compute the \(x\) values as the left (or right) endpoints of each sub-interval: \(x_i = a + i \Delta x\) (or \(x_i = a + (i + 1) \Delta x\)). Knowing these \(x\) values, then compute the \(y\) values for each (these are the heights of each rectangle): \(h_i = f(x_i)\). Having now the width and height of each rectangle, the areas are \(A_i = f(x_i) \Delta x\). Add up the areas, and the approximation is complete.
In the last several minutes of the class, I broke down the geometric interpretation for the definite integrals of a function that is only known by its graph. There are several ways to approach these problems, but I find that identifying simple shapes is probably the most straightforward.



Recent Comments