Note: Strictly speaking, partial fraction decomposition is a technique that is not specific to the task of integration.
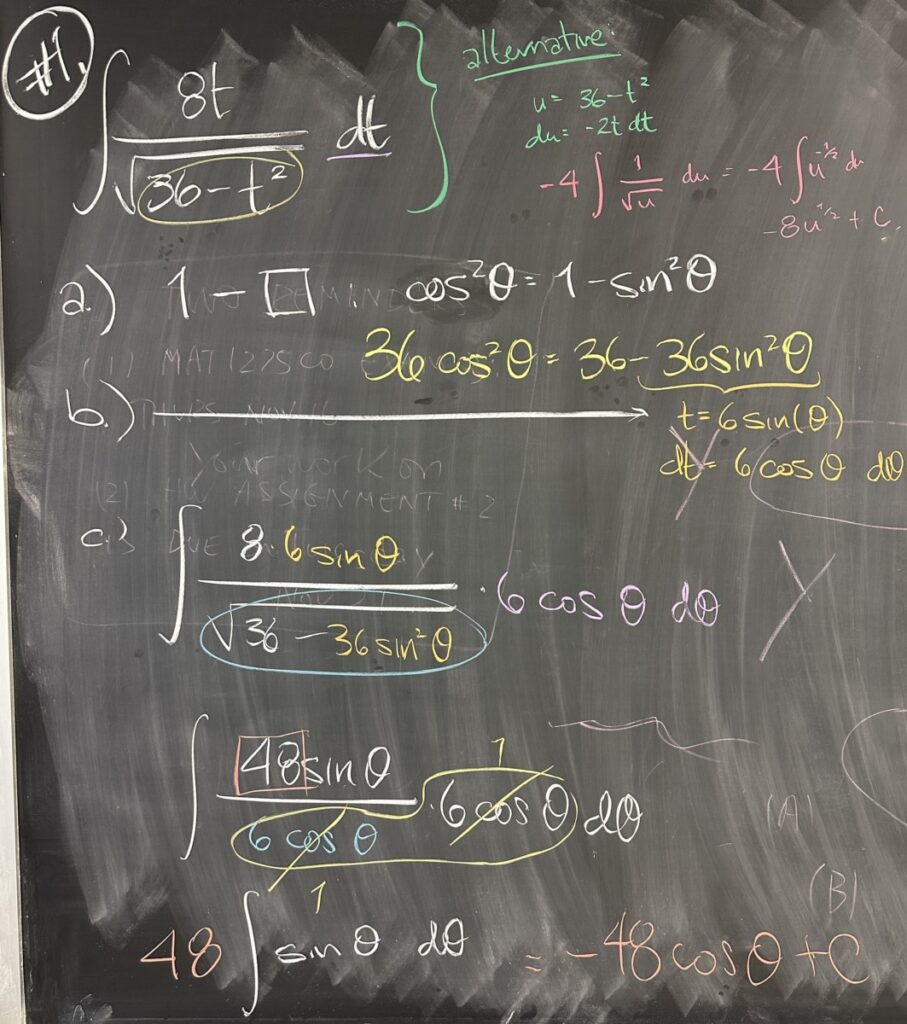
Today’s quiz covered the technique of trig substitution. Part a.) asks for the pythagorean trig identity that would be useful in this integral. Our integral contains \(\sqrt{36 – t^2}\), which corresponds to \(\cos^2(\theta) = 1 – \sin^2(\theta)\) — or with slight modification \(36\cos^2(\theta) = 36 – 36\sin(\theta)\).
In order to fit this form of the pythagorean trig identity, we substitute \(t = 6\sin(\theta)\) and its counterpart \(dt = 6\cos(\theta)\,d\theta\). \[\int \frac{8t}{\sqrt{36-t^2}}\,dt = \int \frac{40\sin(\theta)}{\sqrt{36-36\sin^2(\theta)}}\left(6\cos(\theta)\right)\,d\theta\]
We then further simplify to \(48\int\sin(\theta)\,d\theta = -48\cos(\theta) + C\)
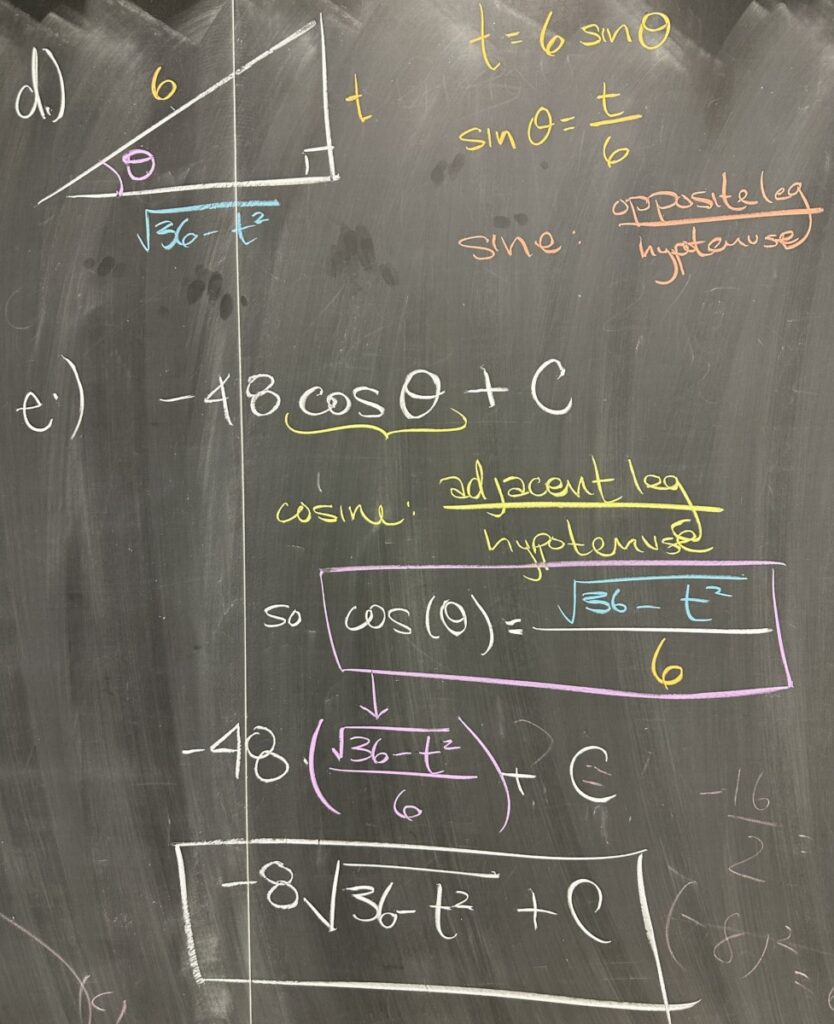
In part d, we then move to geometry in order to convert our answer (currently written in terms of \(\theta\)) in terms of our original variable, \(t\). We start by identifying \(\sin(\theta) = \frac{t}{6}\) from our original substitution. This ratio for sine gives us an image of a right triangle, with \(t\) as the length of \(\theta\)’s opposite leg and \(6\) as the length of the hypotenuse.
Using the Pythagorean Theorem, we know that the leg adjacent to \(\theta\) has length \(\sqrt{36 – t^2}\). With all three lengths known, we can find all of the trig ratios for \(\theta\), and we specifically want cosine: \(\cos(\theta)=\frac{\sqrt{36-t^2}}{6}\) so our final answer for the original integral is \[-48\cos(\theta)+C = -8\sqrt{36-t^2}+C\]
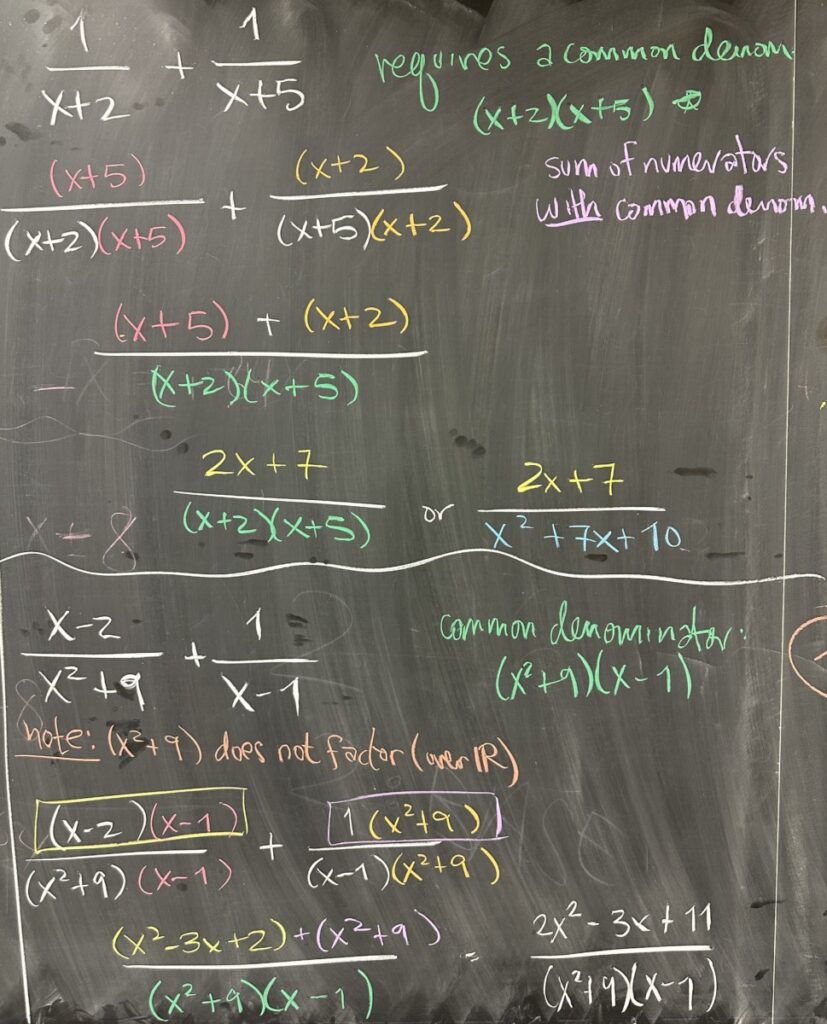
In preparation for Partial Fraction Decomposition, we review a topic that will become very important: adding fractions of polynomials. In both of these examples, we identified a common denominator: \[\frac{1}{x+2}+\frac{1}{x+5} = \frac{1(x+5)}{(x+2)(x+5)} + \frac{1(x+2)}{(x+5)(x+2)} = \frac{2x+7}{x^2+7x+10}\]
and in the second example: \[\frac{x-2}{x^2+9} + \frac{1}{x-1} = \frac{(x-2)(x-1)}{(x^2+9)(x-1)} + \frac{1(x^2+9)}{(x-1)(x^2+9)} = \frac{2x^2-3x+11}{x^3-x^2+9x-9}\]

The technique of Partial Fraction Decomposition is motivated by trying to reverse the process that we just performed on our sums of polynomial fractions. We also borrow the notion of a “proper” fraction to refer to polynomial fractions where the denominator has larger degree than the numerator.
Here we also noted that in our previous examples, the combined fraction always had a denominator that was a product of the separate fractions that we started with. If we are interested in reversing this combination, we must begin by considering the factors present in the denominator.
Recall that factors of a polynomial correspond to the roots of the graph of the polynomial. Real roots correspond to linear factors while complex (pairs of) roots correspond to quadratic factors such as \(x^2+9\) from our earlier example.

Now, a concrete example: decomposing \(\frac{2-x}{x^2+7x+12}\). First, we factor the denominator: \(x^2+7x+12 = (x+3)(x+4)\) and use each factor to create a new fraction: \(\frac{\text{?}}{x+3}\) and \(\frac{\text{?}}{x+4}\). The question then arises, what should our numerators be?
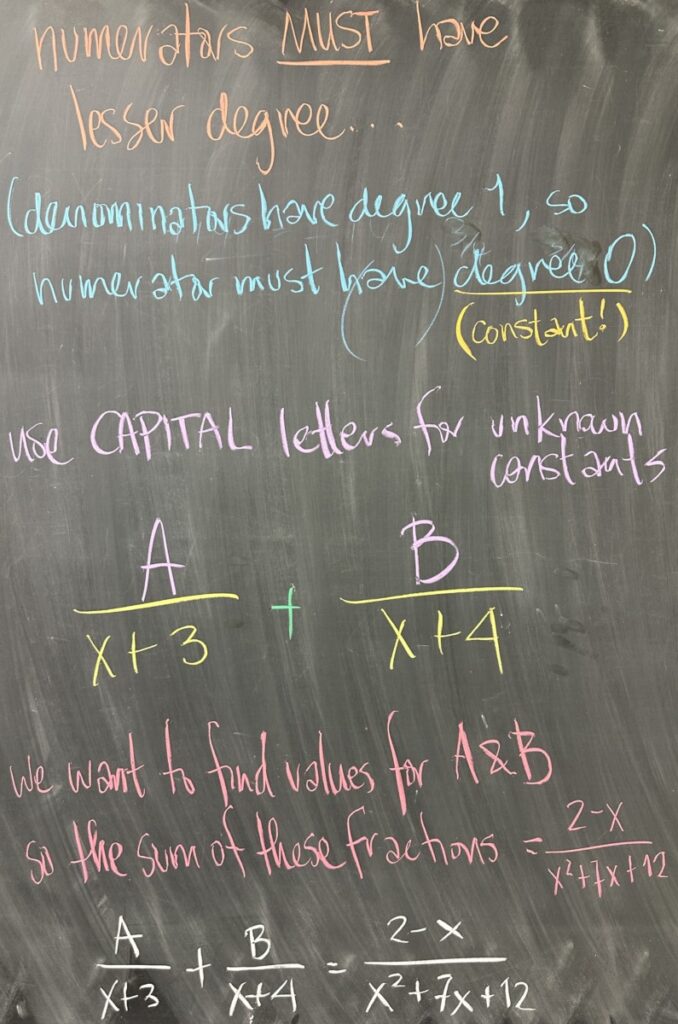
Since we are only talking about “proper” fractions, this restricts our numerator to a degree zero polynomial (since the denominator has degree one and “proper” means the numerator having smaller degree). “Zero degree polynomials” only have a degree-zero term, which must be a constant. With the numerators determined to be constant (\(A\) for the first, and \(B\) for the second), we conclude that: \[\frac{A}{x+3} + \frac{B}{x+4} = \frac{2-x}{x^2+7x+12}\]
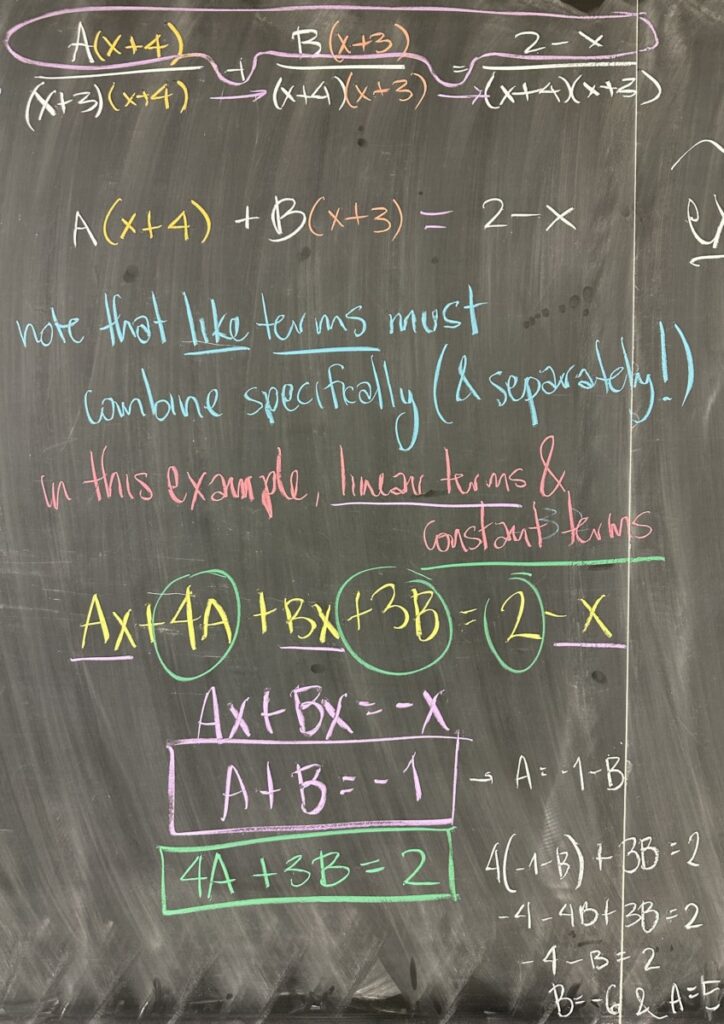
By converting all fractions to the same denominator, we conclude that the equation is determined by the numerators: \[A(x+4) + B(x+3) = 2 – x\]
Note here that this equation must be true for all \(x\) and we are actually trying to determine values for \(A\) and \(B\).
Also note that our like terms on the left side of this equation must add up to specific values on the right side. In fact, each of the different terms gives us its own equation: \(A + B = -1\) from the \(x\) terms and \(4A + 3B = 2\) from the constant terms.
Use your favorite method to solve this system of two equations with two unknowns: substitution (as shown) or elimination. We conclude \(B = -6\) and \(A = 5\) so \[\frac{5}{x+3} + \frac{-6}{x+4} = \frac{2-x}{x^2+7x+12}\]
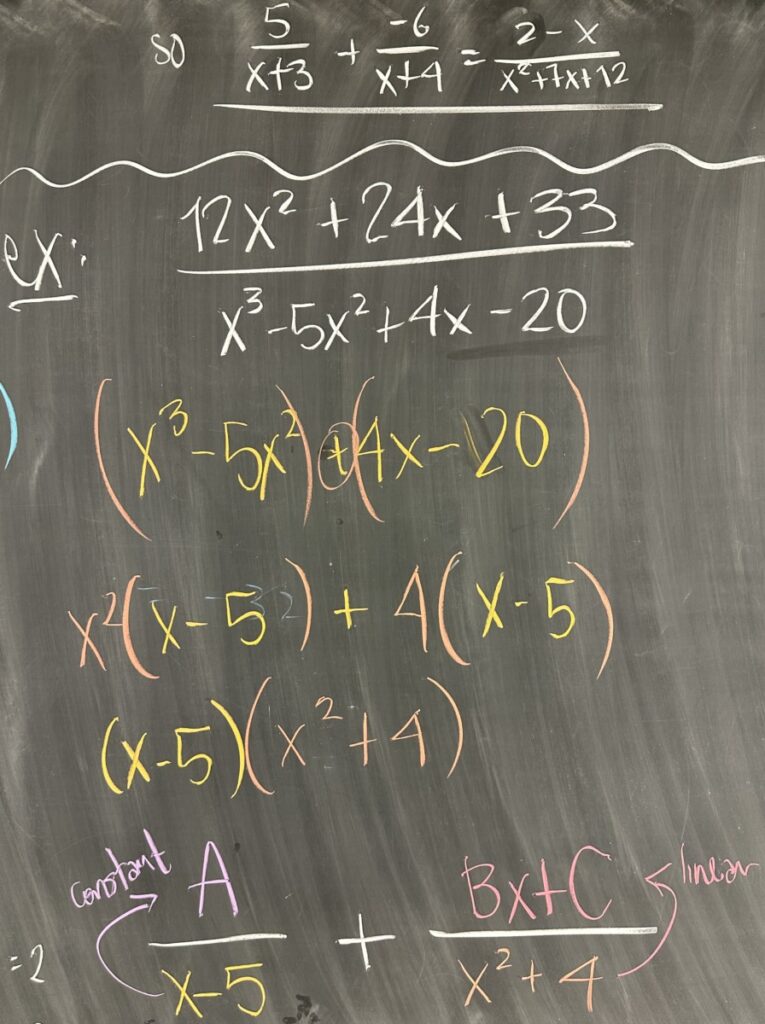
In a quick example of what to do in higher degree situations, we look at \(\frac{12x^2+24x+33}{x^3-5x^2+4x-20}\). As always, we must factor the denominator in order to identify the factors that will form the denominators of our decomposition. With the factors \(x-5\) and \(x^2-4\), we then ask the necessary question: what should our numerators be? In the case of \(x-5\), which is linear, the numerator must have smaller degree and must therefore be constant: \(A\). In the case of \(x^2+4\), a quadratic (degree: 2), the numerator can be linear at most (degrees 1 and 0 are less than degree 2): \(Bx + C\).



Recent Comments