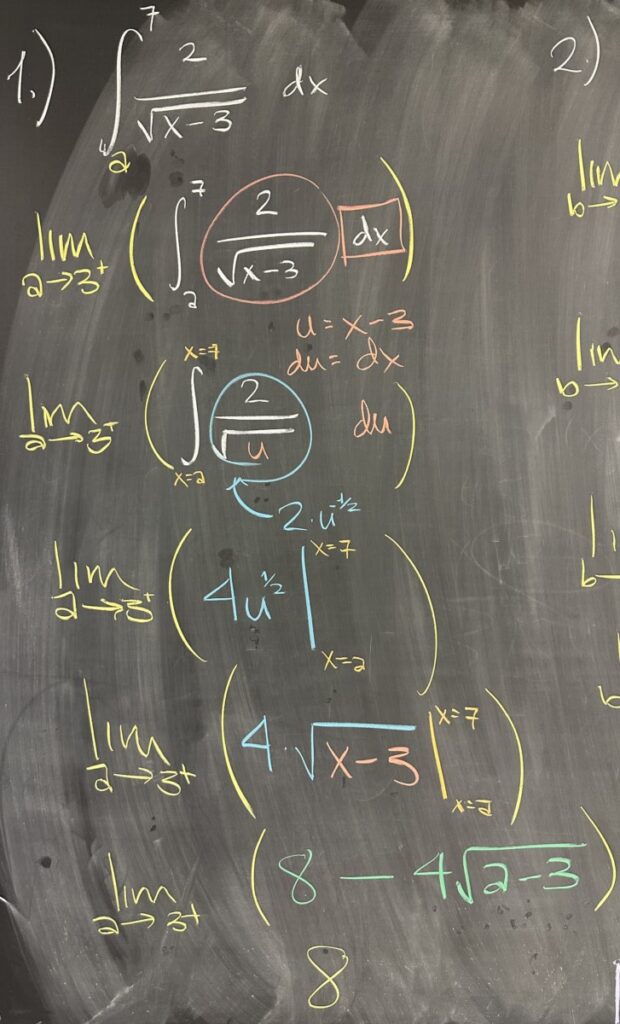
Today’s quiz covered the topic of improper integrals. The first improper integral uses a function, \(f(x) = \frac{2}{\sqrt{x-3}}\), that has a vertical asymptote at \(x=3\). This \(x\)-value is also one of our bounds, which is what makes this an improper integral.
The instructions on the quiz explicitly required rewriting the integral as a limit, and this is necessary to satisfy the conditions for the Fundamental Theorem of Calculus. Using the interval \([a,7]\) as \(a\to 3^+\), rewrite the integral: \[\int_3^7 \frac{2}{\sqrt{x-3}}\,dx = \lim_{a\to 3^+}\left(\int_a^7\frac{2}{\sqrt{x-3}}\,dx\right)\]
It’s important to note that we only consider the one-sided limit as \(a\to3^+\) because \(a\) is the lower bound of our interval and we are only interested in values larger than \(3\). This is particularly relevant because \(f(x)\) isn’t defined for \(x<3\).
Since we can apply the Fundamental Theorem for \([a,7]\), we start by finding the antiderivative of \(f(x)\) by u-substitution with \(u = x-3\) and \(du = dx\): \[\lim_{a\to 3^+}\left(\int_a^7\frac{2}{\sqrt{x-3}}\,dx\right) = \lim_{a\to 3^+}\left(2\int_{x=a}^{x=7}u^{-\frac{1}{2}}\,du\right)\]
Using the power rule for antiderivatives, we find \(2\int u^{-\frac{1}{2}}\,du = 2\cdot2\sqrt{u} = 4\sqrt{x-3}\): \[\lim_{a\to 3^+}\left(2\int_{x=a}^{x=7}u^{-\frac{1}{2}}\,du\right) = \lim_{a\to 3^+}\left(4\sqrt{x-3}\,\Bigg\vert_a^7\right)\]
Then finishing the Fundamental Theorem and finding the limit: \[\lim_{a\to 3^+}\left(4\sqrt{x-3}\,\Bigg\vert_a^7\right) = \lim_{a\to 3^+}\left(4\sqrt{4} – 4\sqrt{a-3}\right) = 8 – 0\]
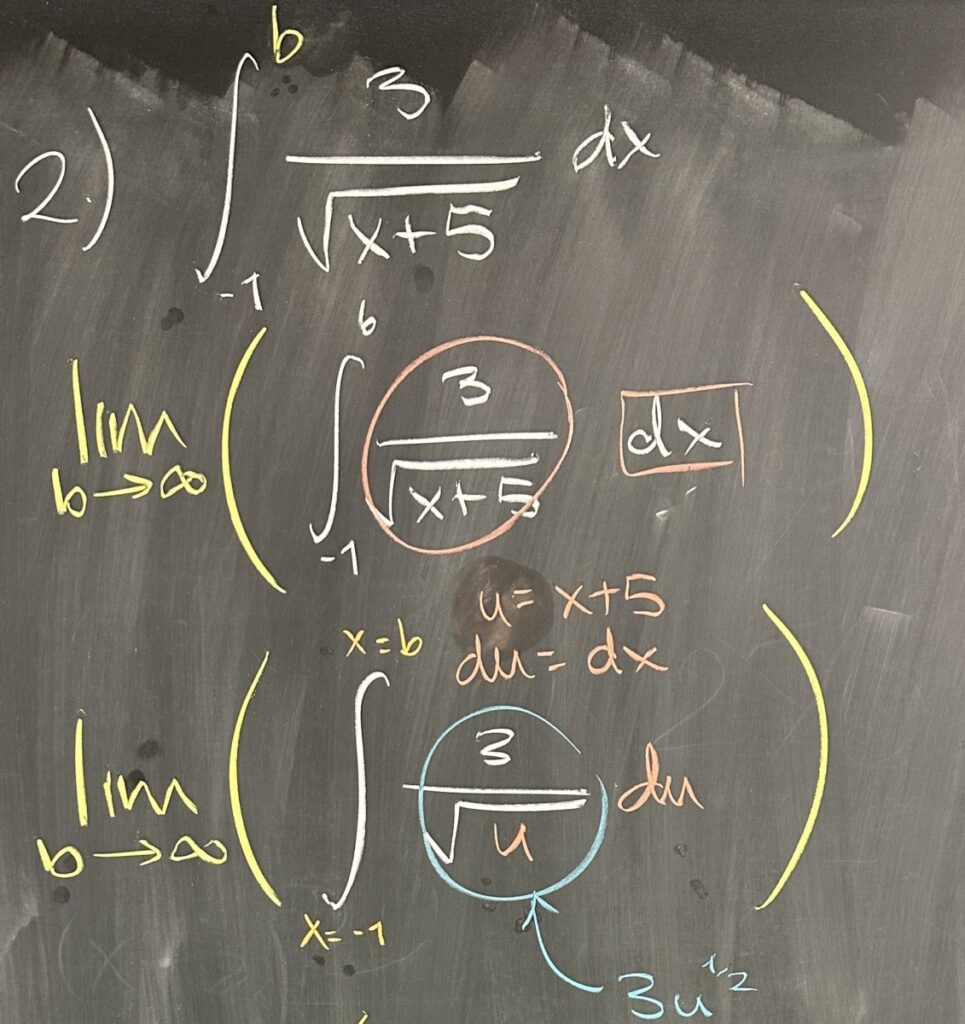
The second integral is improper, not because of a vertical asymptote — as in the previous problem — but because the bounds are \([-1,\infty)\). The Fundamental Theorem of Calculus requires a closed interval (including both endpoints), but we certainly cannot include \(x=\infty\) in the domain for \(f(x) = \frac{3}{\sqrt{x+5}}\) (as it would be for any function).
So instead we consider the interval \([-1,b]\) as \(b\to\infty\): \[\int_{-1}^\infty \frac{3}{\sqrt{x+5}}\,dx = \lim_{b\to\infty}\left(\int_{-1}^b \frac{3}{\sqrt{x+5}}\,dx\right)\]
Then we can apply the Fundamental Theorem, starting with u-substitution \(u = x+5\) and \(du = dx\): \[\lim_{b\to\infty}\left(\int_{-1}^b \frac{3}{\sqrt{x+5}}\,dx\right) = \lim_{b\to\infty}\left(\int_{x=-1}^{x=b} \frac{3}{\sqrt{u}}\,du\right)\]

Noting that the antiderivative of \(3u^{-\frac{1}{2}}\) is \(3\cdot 2 \sqrt{u}\), and further that \(u = x+5\) so that makes \(6\sqrt{x+5}\): \[\lim_{b\to\infty}\left(\int_{-1}^b \frac{3}{\sqrt{u}}\,du\right) = \lim_{b\to\infty}\left(6\sqrt{b+5} – 6\sqrt{-1+5}\right)\]
Although the square-root function increases quite slowly, it is still unbounded, so \(\displaystyle \lim_{b\to\infty} \sqrt{b+5} = \infty\). As a result, we conclude that this improper integral is divergent.
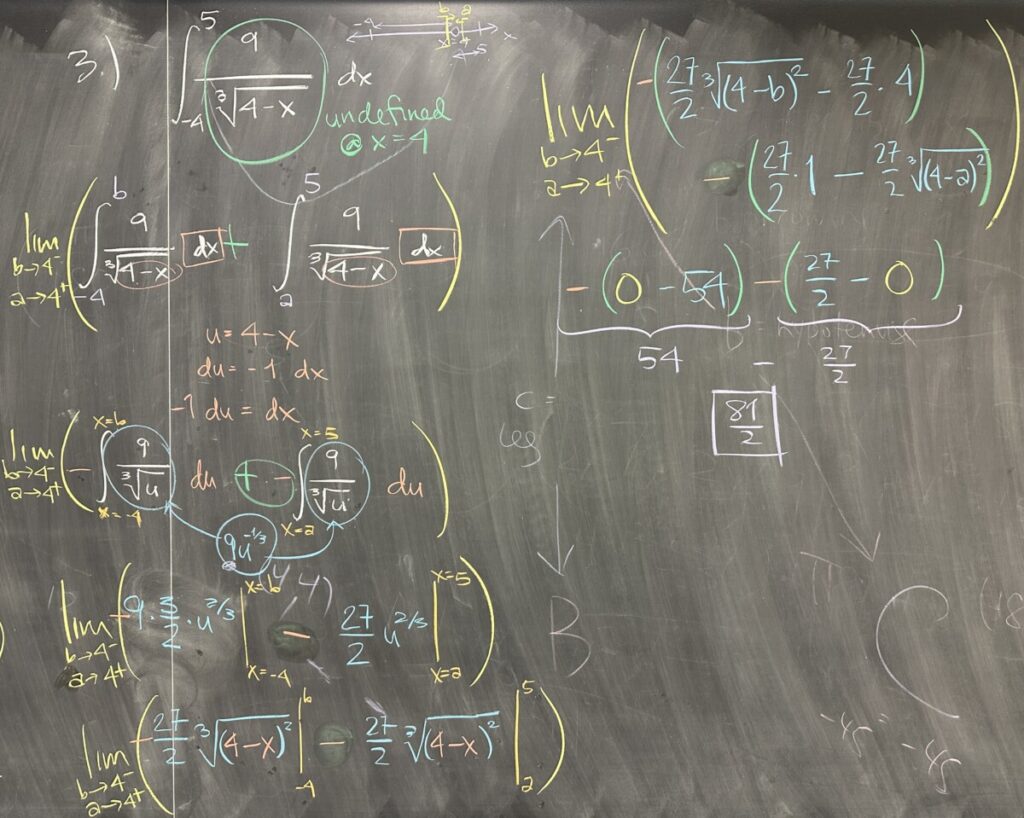
In the third problem, our definite integral spans the interval \([-4,5]\) which includes a gap in the domain: \(x \neq 4\). Splitting the interval at \(x=4\) we have \([-4,4)\cup(4,5]\), which we must convert to closed intervals for the purpose of meeting the requirements of the Fundamental Theorem: \([-4,b]\cup[a,5]\) as \(b\to 4^-\) and \(a\to 4^+\).
Being able to use the Fundamental Theorem on the intervals \([-4,b]\) and \([a,5]\) means we need the antiderivative of \(f(x) = \frac{9}{\sqrt[3]{4-x}}\). Starting with u-substitution \(u = 4-x\) and \(du = -1\,dx\), we then find the antiderivative: \[\int -9u^{\frac{1}{3}}\,du = \frac{-27}{2}\sqrt[3]{u^2} = \frac{-27}{2}\sqrt[3]{(4-x)^2}\]
Over the interval \([-4,b]\) we have \[\int_{-4}^b \frac{9}{\sqrt[3]{4-x}}\,dx = \frac{-27}{2}\sqrt[3]{(4-b)^2} – \left(\frac{-27}{2}\sqrt[3]{(4-(-4))^2}\right)\]
And over the interval \([a,5]\) we have \[\int_a^5 \frac{9}{\sqrt[3]{4-x}}\,dx = \frac{-27}{2}\sqrt[3]{(4-5)^2} – \left(\frac{-27}{2}\sqrt[3]{(4-a)^2}\right)\]
Finally, we have to consider what happens as \(a\to 4^+\) and \(b\to 4^-\). In each case we have \[\lim_{a\to 4^+}\sqrt[3]{(4-a)^2} = 0 \text{ and } \lim_{b\to 4^-}\sqrt[3]{(4-b)^2} = 0\]
This makes our definite integrals: \[\lim_{b\to 4^-}\left(\frac{-27}{2}\sqrt[3]{(4-b)^2} – \frac{-27}{2}\sqrt[3]{64}\right) = 54\]
And: \[\lim_{a\to 4^+}\left(\frac{-27}{2}\sqrt[3]{1} – \left(\frac{-27}{2}\sqrt[3]{(4-a)^2}\right)\right) = \frac{-27}{2}\]
So our total area is \(54 + \frac{-27}{2} = \frac{81}{2}\).
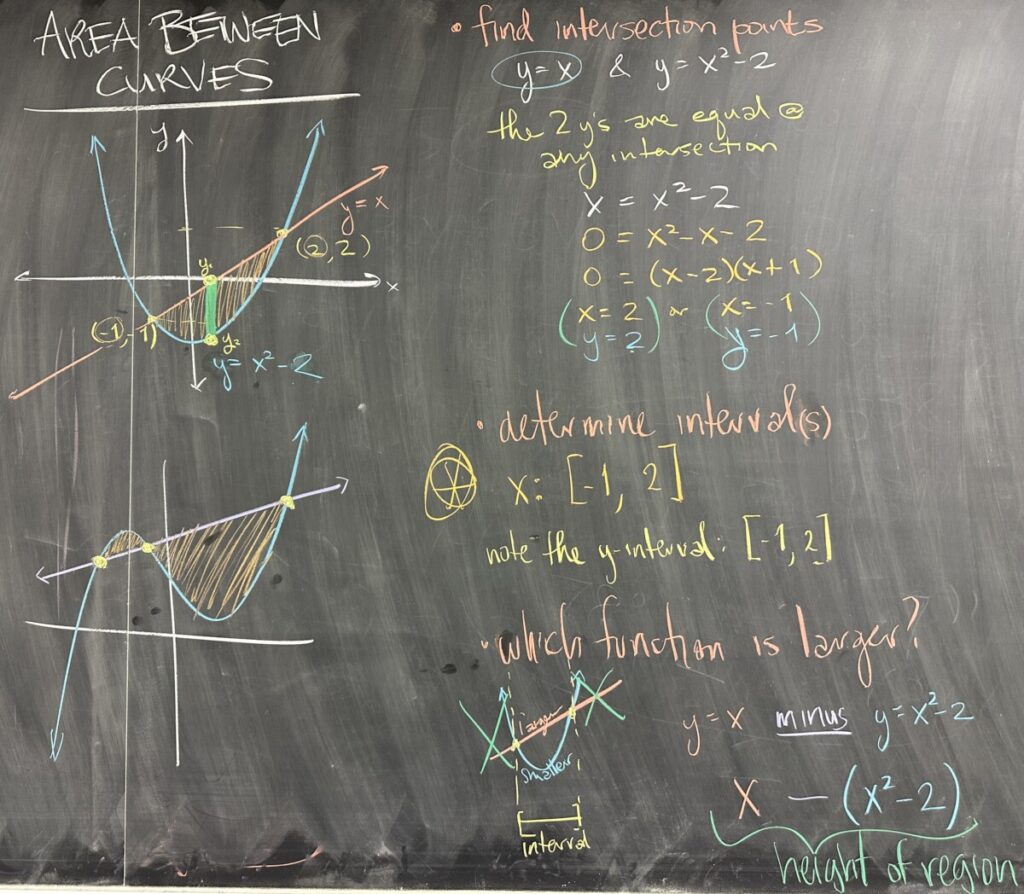
Moving on to today’s main topic, we consider what happens when we want to measure the area between two curves. In order for two curves to form a fully enclosed region, they must intersect at least twice. (See the illustrations of two curves intersecting twice and intersecting more than twice.)
The intersections between given curves will be the first thing that we want to find. In the first example, our curves are a line: \(y = x\) and a parabola: \(y=x^2-2\). Using substitution, we replace \(y\) in the second equation with \(x\) (because the first equation tells us \(y\) and \(x\) are equal, and are therefore interchangeable). This leaves us with the equation \(x = x^2 – 2\) which ultimately has solutions \(x = -1\) and \(x=2\).
It is important to note that intersections are points, and as such there are both \(x\) and \(y\)-values for each. Our intersections in the example occur at \((-1,-1)\) and \((2,2)\). If we look at the intervals that are created for both \(x\) and \(y\) we notice that they are both \([-1,2]\) — however these two intervals (\(-1\leq x \leq 2\) and \(-1 \leq y \leq 2\)) only form a legitimate boundary for the region in the \(x\)-direction.
Note: \(y\) actually dips below \(-1\) in our region, so \(-1 \leq y \leq 2\) will not actually work as an interval for this example.
Having then settled on an interval for \(x\), we must then consider which of the two curves is “larger” and which is “smaller” on the interval. For \(-1 \leq x \leq 2\), we see that the line has larger \(y\)-values than the parabola. This means that the “height function” for our region will be described by the difference “larger minus smaller”, or or in this case: \((x) – (x^2-2)\).
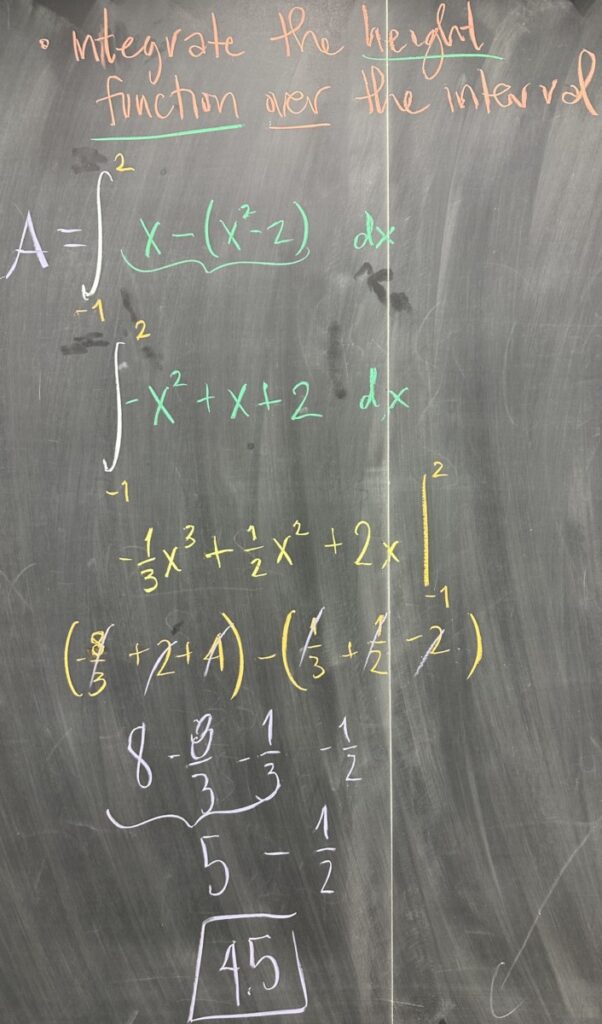
Once we have determined our interval and the height function, we are ready to compute the area of the region as a definite integral. Integrating the height function \(x-x^2+2\) over the interval \(-1\leq x\leq 2\) we have: \[\int_{-1}^2 -x^2+x+2\,dx = -\frac{1}{3}x^3 + \frac{1}{2}x^2 + 2x \,\Bigg\vert_{-1}^2\]
Applying the Fundamental Theorem: \[-\frac{1}{3}x^3 + \frac{1}{2}x^2 + 2x \,\Bigg\vert_{-1}^2 = \left(-\frac{8}{3}+2+4\right) – \left(\frac{1}{3} + \frac{1}{2} – 2\right) = \frac{9}{2}\]
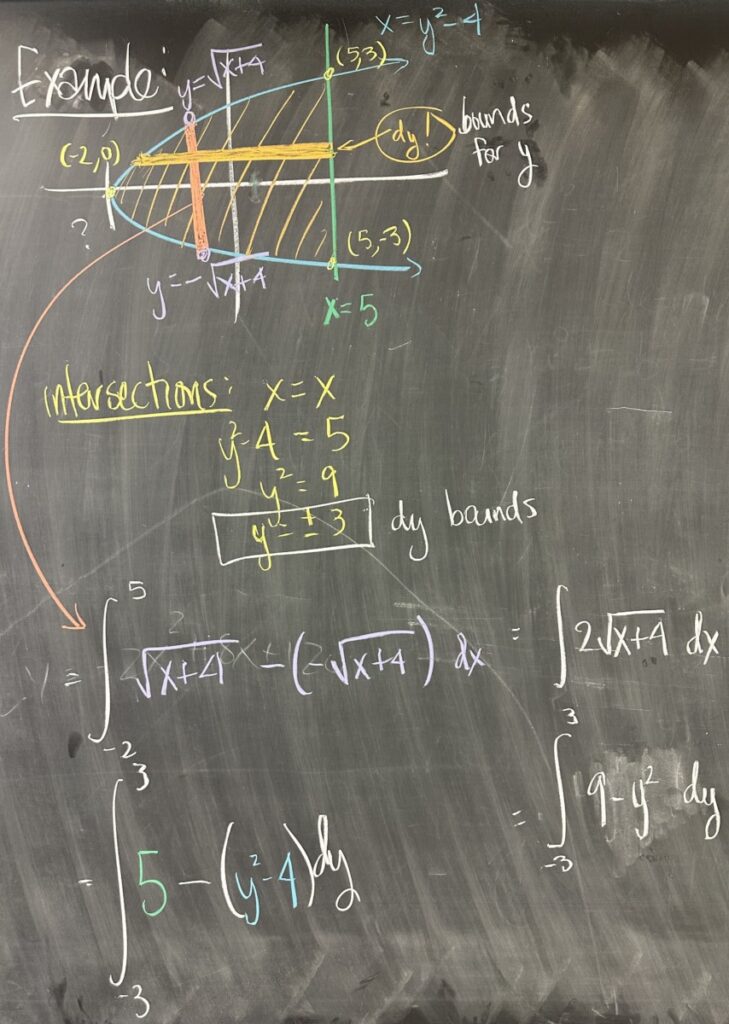
In our final example, we consider the two curves \(x = 5\) (a vertical line) and \(x = y^2 – 4\) (a parabola opening to the right). Since \(x = 5\) from the first equation, we can substitute in the second equation to get \(5 = y^2 – 4\), which has solutions \(y = 3\) and \(y = -3\). As points, the intersections are \((5,3)\) and \((5,-3)\).
If we consider the intervals for \(x\) and \(y\) given by these two intersections, we have \(5 \leq x \leq 5\) (in other words, just \(x = 5\)) and \(-3 \leq y \leq 3\). Clearly \(x = 5\) is not enough to cover the entire region, and by looking at the graph of the region, we see that the minimum value for \(x\) in the region is \(-4\). This means that the \(x\)-interval for the region is actually \([-4,5]\).
With our \(x\)-interval in hand, we move on to compute the “height function” for our region. Complicating matters is the fact that the “top” (or “larger”) curve is actually the top half of the parabola — and the “smaller” curve curve is the bottom half of the same parabola. Computing the height of our region means subtracting \(y\)-values, so we must express our “two” curves (each one is part of the same parabola) as \(y = f(x)\) instead of \(x = y^2 – 4\). Solving for \(y\) in the parabola equation results in \(y = \pm\sqrt{x+4}\), so we have the “larger” curve \(y=\sqrt{x+4}\) and “smaller” curve \(y=-\sqrt{x+4}\).
This makes our “height function” \( \sqrt{x+4} – (-\sqrt{x+4}) = 2\sqrt{x+4}\), which we integrate over our interval \([-4,5]\): \[\int_{-4}^5 2\sqrt{x+4}\,dx\]
On the other hand, in cases such as this (where \(x\) is expressed as a function of \(y\)), it can be better to think of \(y\) as our independent variable instead of \(x\).
This means that we would integrate with respect to \(y\) (using \(dy\)) and use the interval for \(y\) (\([-3,3]\)). In this case, we consider the “larger” and “smaller” curves with respect to their \(x\)-values (in the \(x\)-direction, “larger” is to the right and “smaller” is to the left). For our region, the vertical line is always to the right of the parabola, making it the “larger” curve. As a result, our “height function” (in this direction, it’s more of a “width function”) is \((5) – (y^2-4) = 9-y^2\). Over our interval \(-3 \leq y \leq 3\) we compute the area of the region as \[\int_{-3}^3 9-y^2\,dy\]
These two integrals compute the area of the same region, and should therefore result in the same value. Which of these two integrals would you rather work with?



Recent Comments