Category: Series (Page 2 of 4)

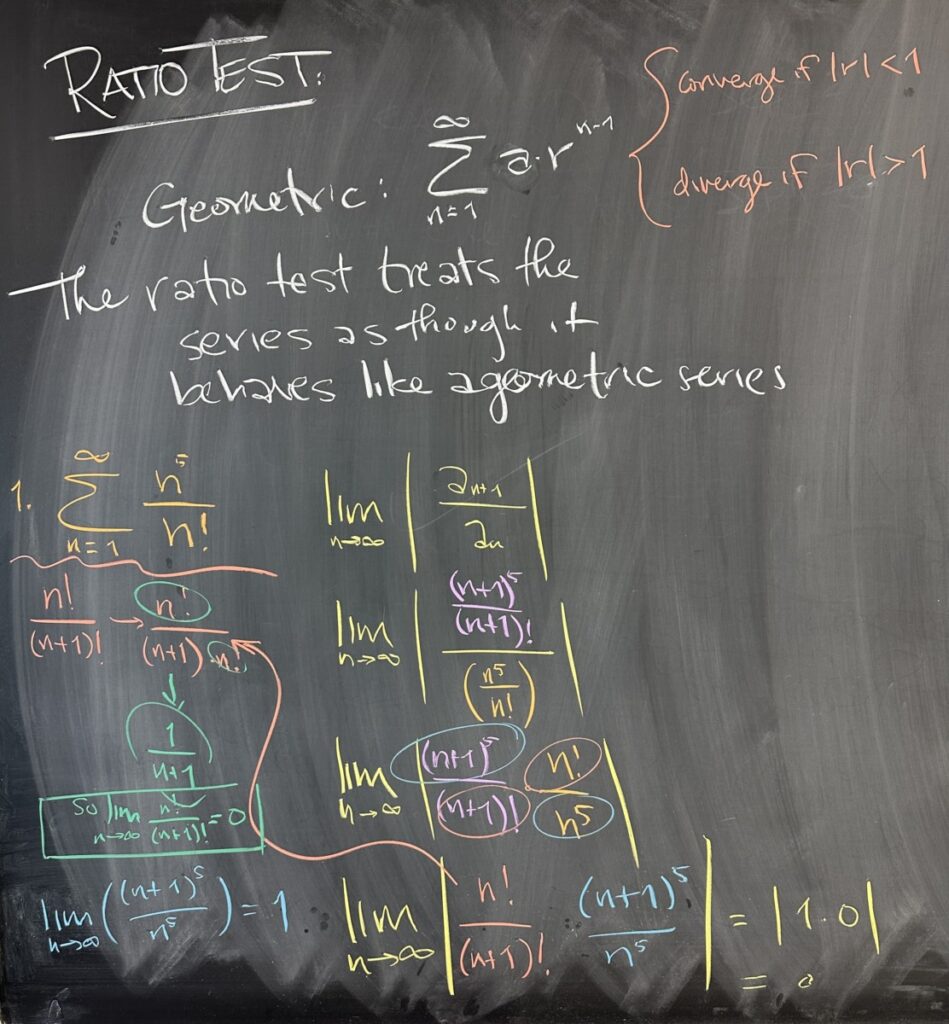
Before talking about today’s quiz, I asked the class to recall the motivation behind the Ratio Test. We will see many series with sequences that are “almost” geometric. That is to say, sequences that don’t have a strictly common ratio — but as n gets very large, the sequence has something very close to a common ratio. (In the last set of notes, I called this a “common-ish” ratio.)

Well, today’s quiz didn’t go as expected. (If you were there, you know.)

So, instead we did some examples together! Our first example is an alternating series, with absolute sequence \(b_n = \dfrac{2n^3-1}{\sqrt{9n^4-n}}\).

Today’s quiz focused on the Limit Comparison Test from last week.