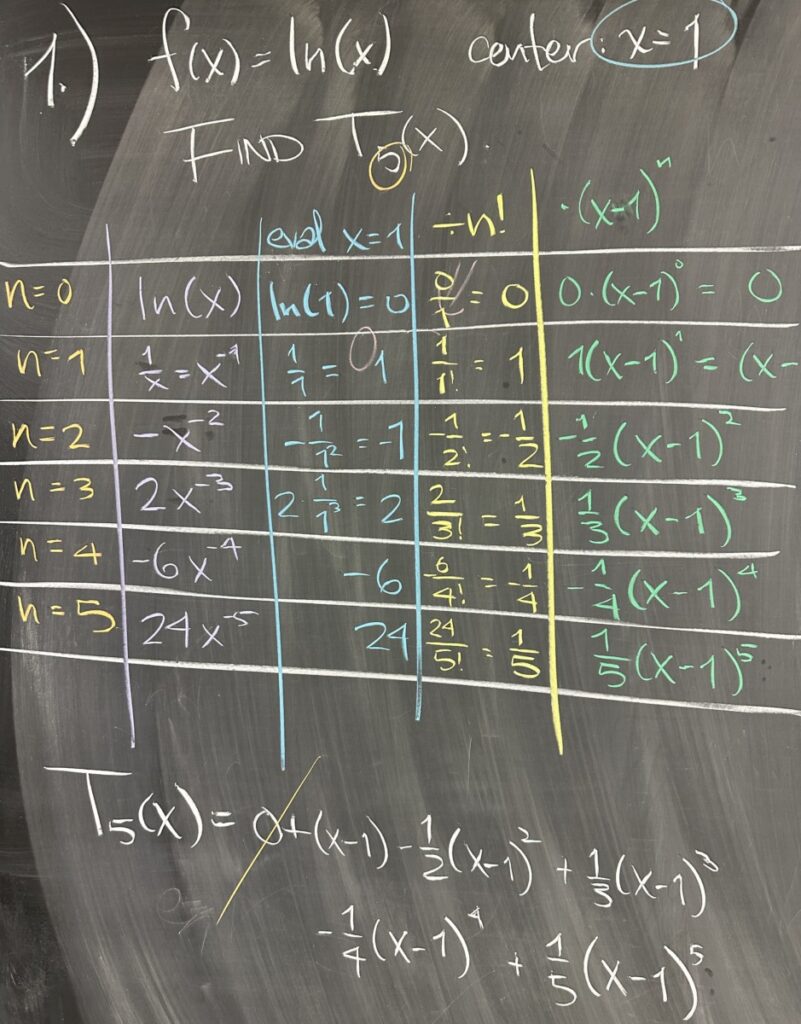
Today’s quiz consisted of a single problem: find the fifth-degree Taylor Polynomial approximation of the function
Parker | D034 | Fall 2023
Lectures in the “Series” unit.
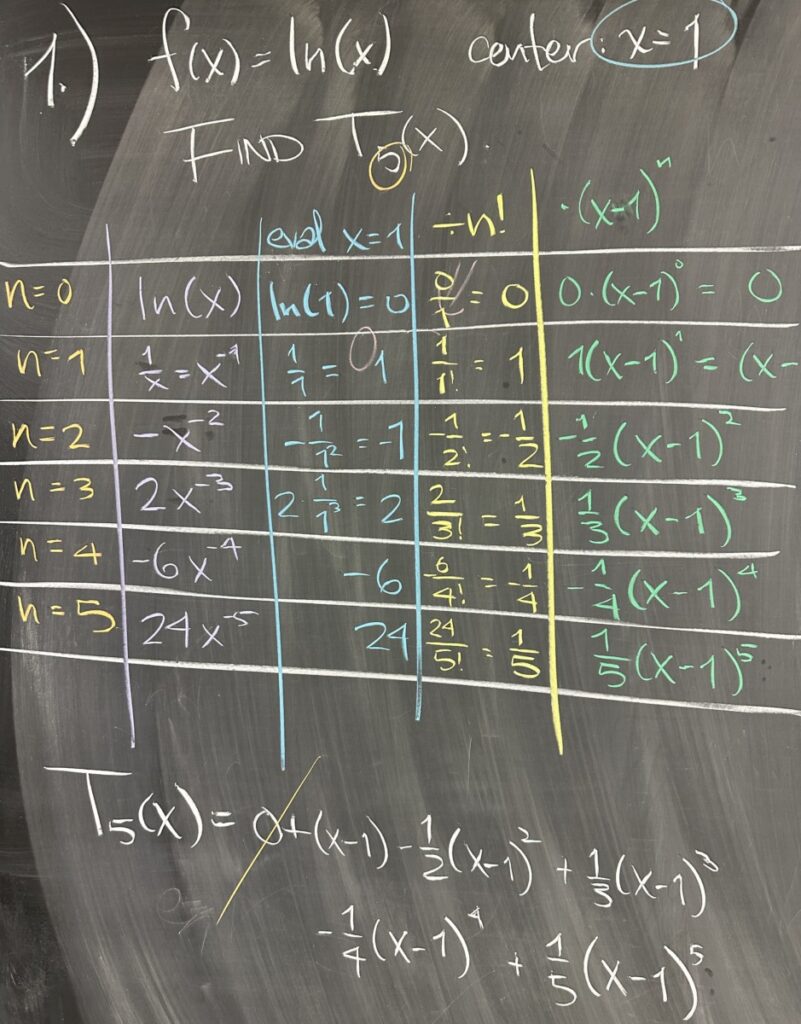
Today’s quiz consisted of a single problem: find the fifth-degree Taylor Polynomial approximation of the function
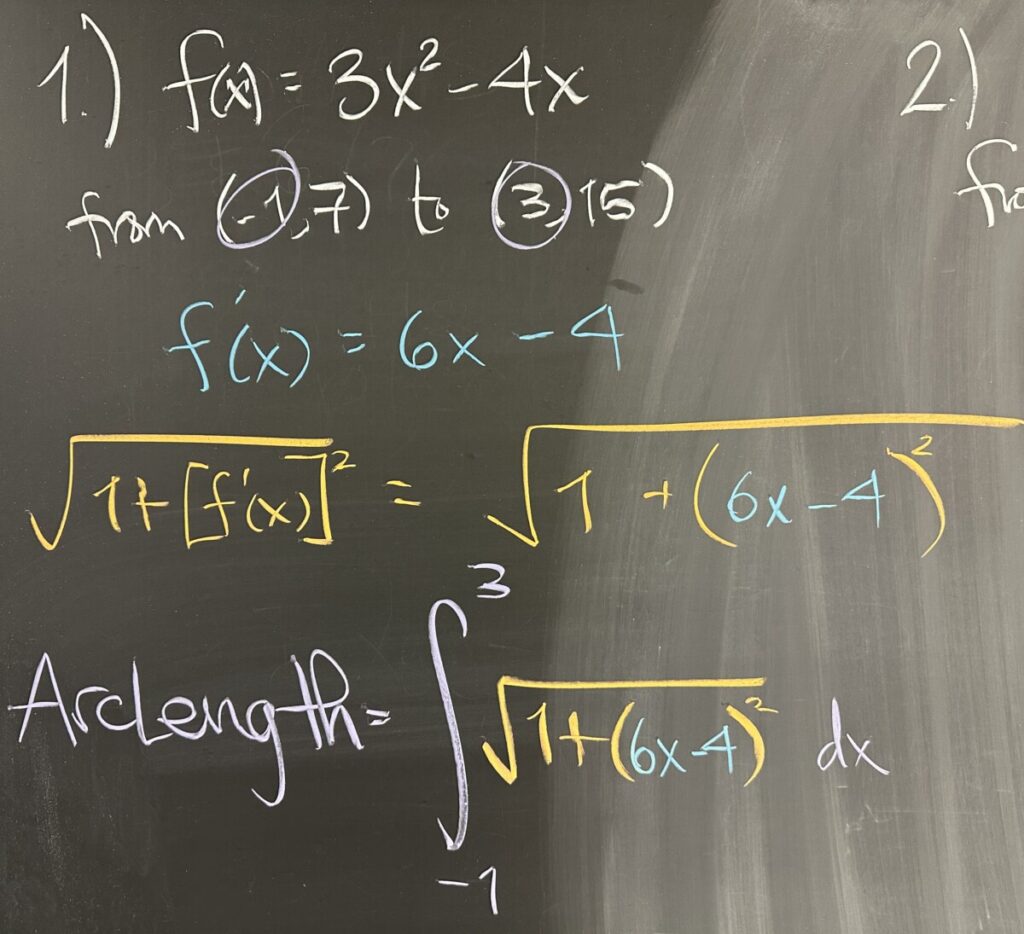
Today’s quiz contained three questions about arc length. The entire problem consisted of setting up (but not evaluating) the integral for arc length of the given functions. Recall that the arc length of
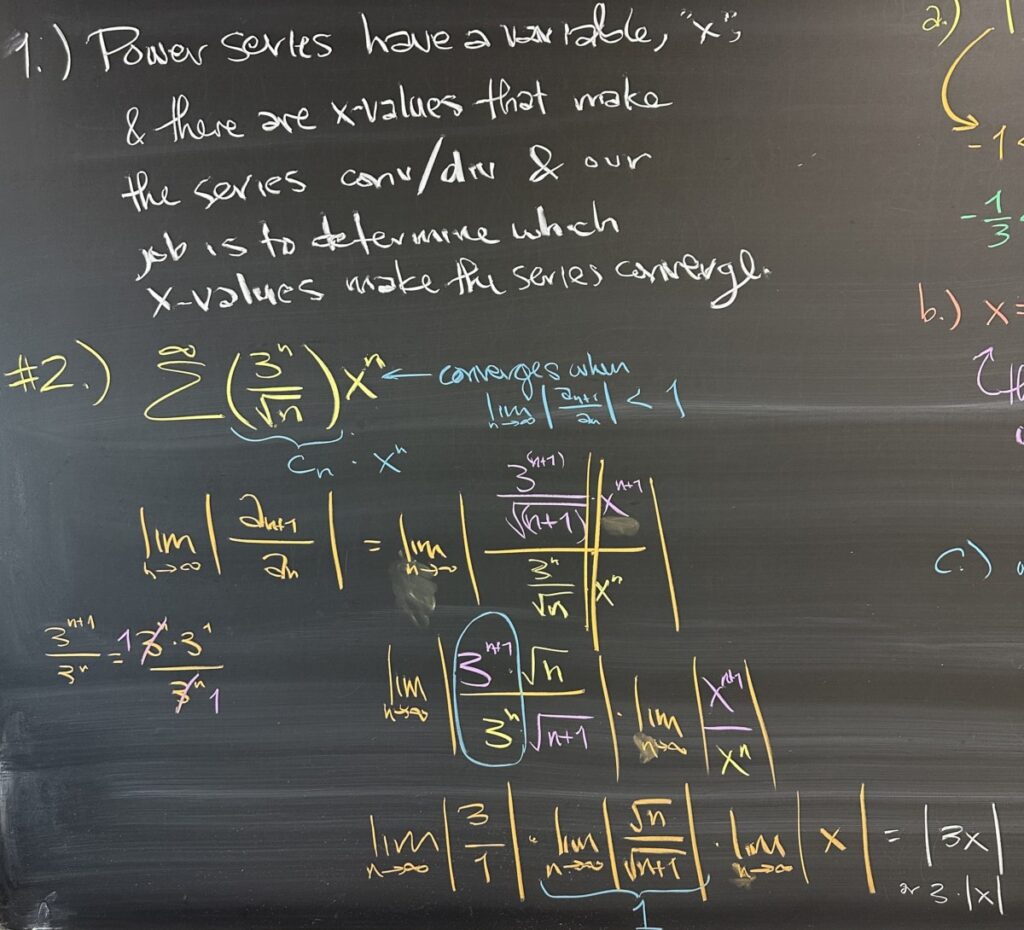
After today’s quiz, we started by talking about what makes “power series” different from the series that we’ve been working with so far this semester. The presence of
© 2025 MAT1575 Calc II F23
Theme by Anders Noren — Up ↑
Recent Comments