Category: Integrals (Page 4 of 5)

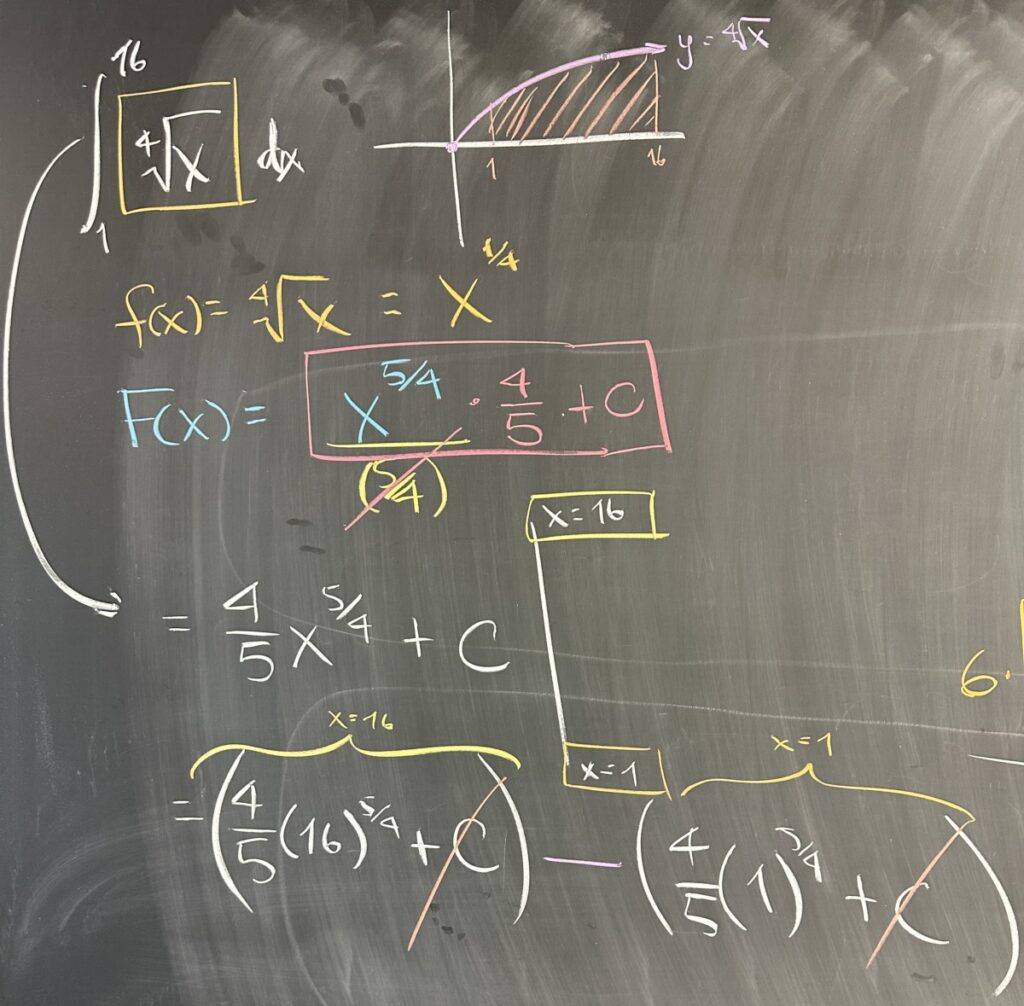
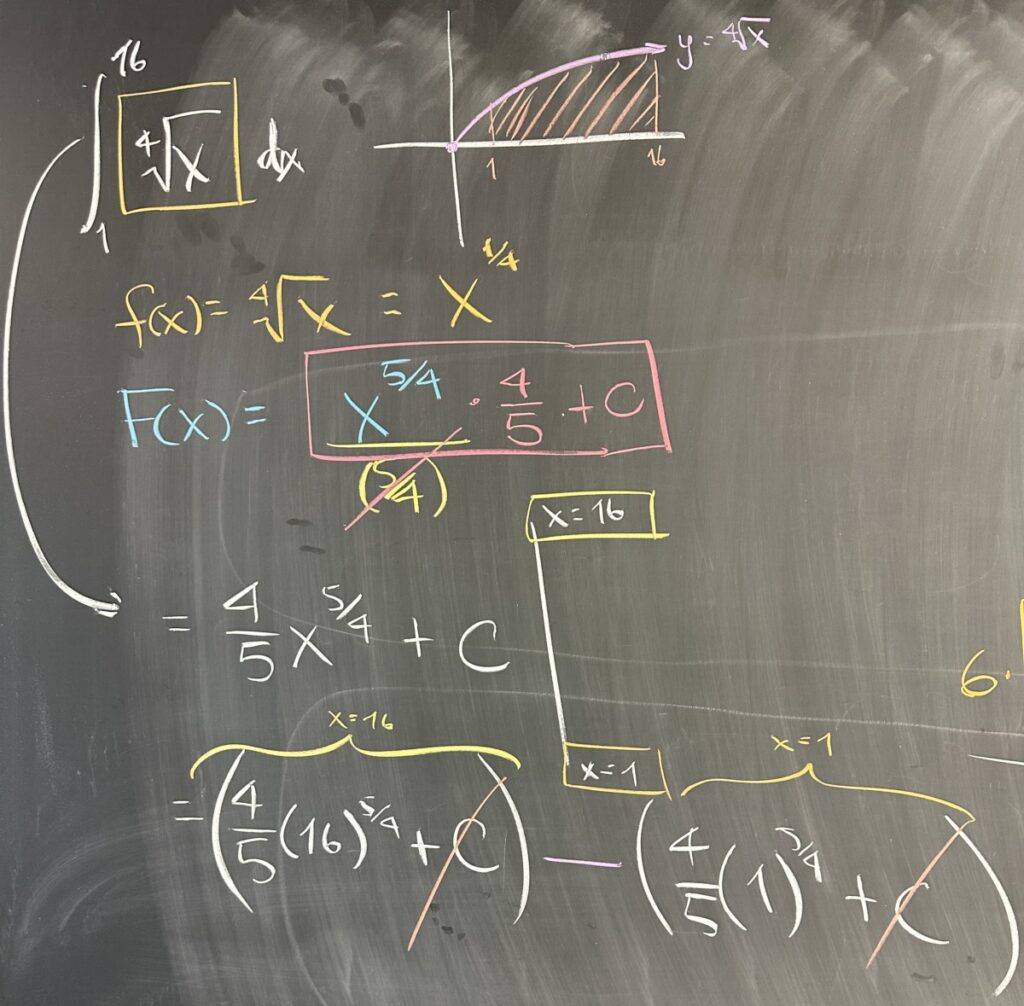
The first quiz problem is a definite integral. We started by thinking about what the function $f(x)=\sqrt[4]{x}$ looks like when graphed, with the bounds $x=1$ and $x=16$. This region is not a “nice” geometric shape — so computing the area will require the Fundamental Theorem of Calculus.

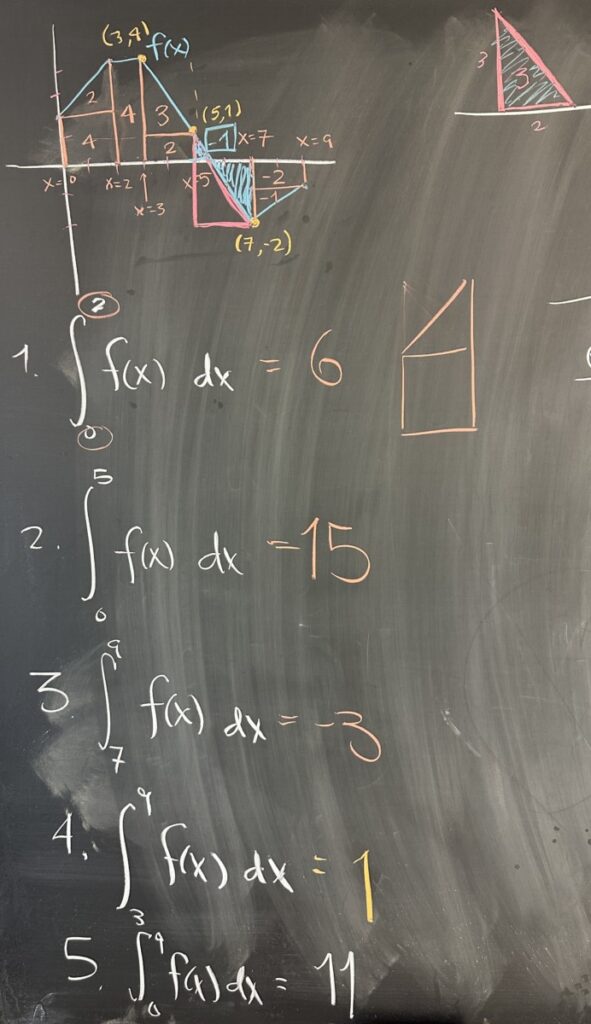
Today’s quiz focused on the interpretation of our notation: ${\displaystyle {\int }_a^{b}f(x)dx}$. This notation refers to the area between $f(x)$ and the $x$-axis, from $x=a$ to $x=b$.

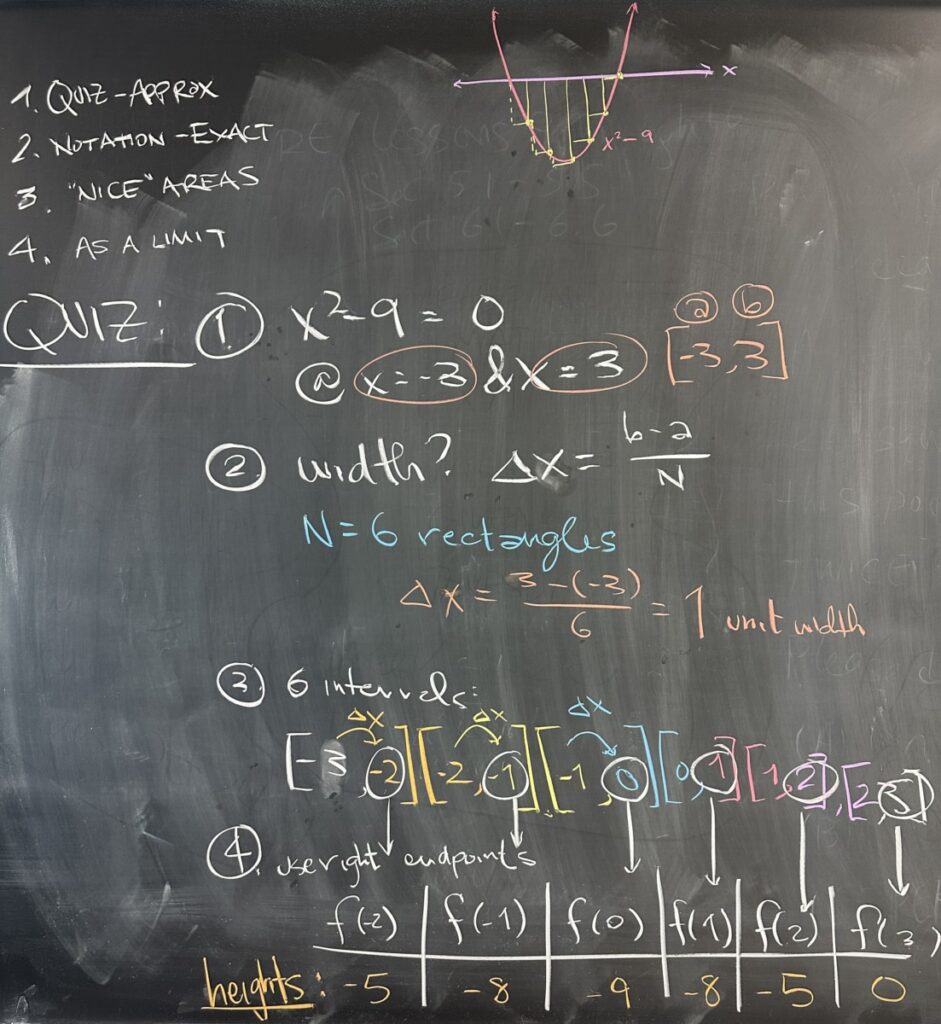
Today’s quiz covered the Riemann Sum. The given function was $f(x)=x^2–9$, and you were asked to identify where the function intersected the $x$-axis. These two intersections were then used as the start and end of our interval for approximating the area bounded by $f(x)$.