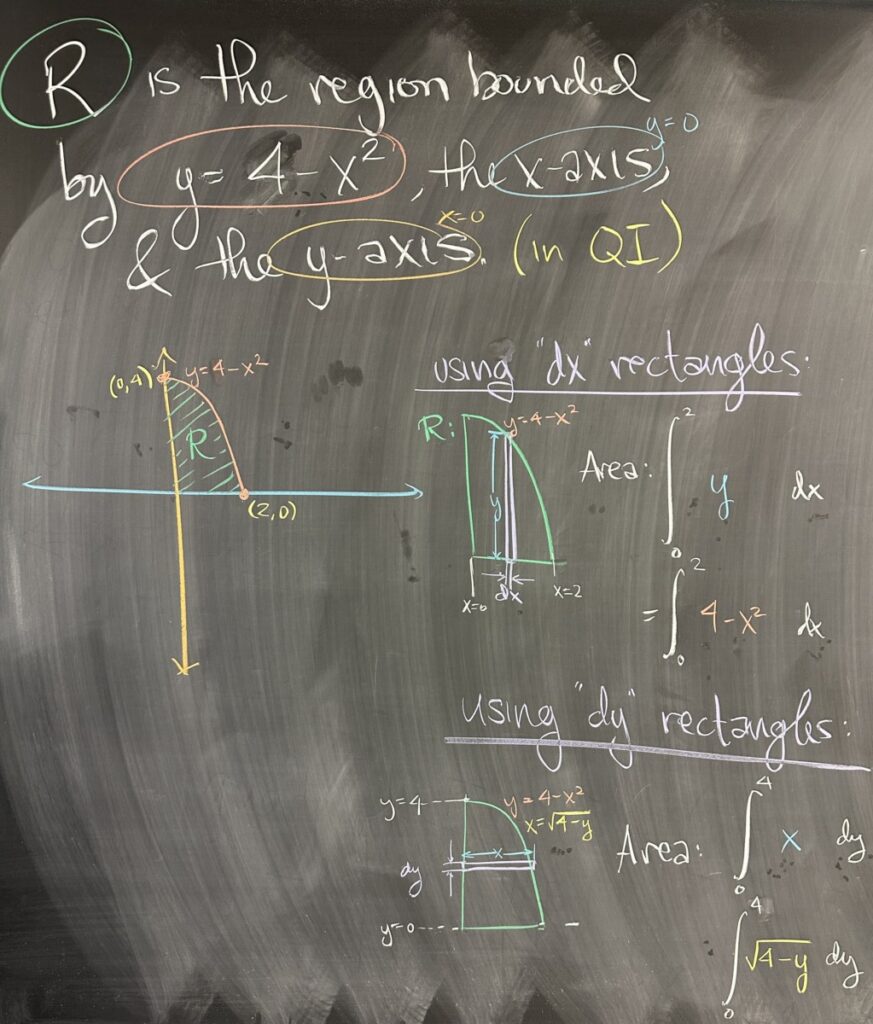
For all of today’s examples, we will use the same region \(R\) — bounded (in the first quadrant) by the \(x\)-axis, \(y\)-axis, and the parabola \(y = 4-x^2\).
We can compute the area of \(R\) in two different ways: using vertical “dx” rectangles or by using horizontal “dy” rectangles.
Using “dx” rectangles, we integrate the height of the region as \(x\) goes from \(0\) to \(2\). The height of the region is measured in the \(y\) direction, as the difference between the top (\(y=4-x^2\)) and bottom (\(y=0\)) boundaries of the region: \[\int_0^2 4-x^2\,dx\]
Using “dy” rectangles, we integrate the width of the region as \(y\) goes from \(0\) to \(4\). The width of the region is measured in the \(x\)-direction, as the difference between the right (\(x=\sqrt{4-y}\)) and left \(x=0\) boundaries of the region: \[\int_0^4 \sqrt{4-y}\,dy\]
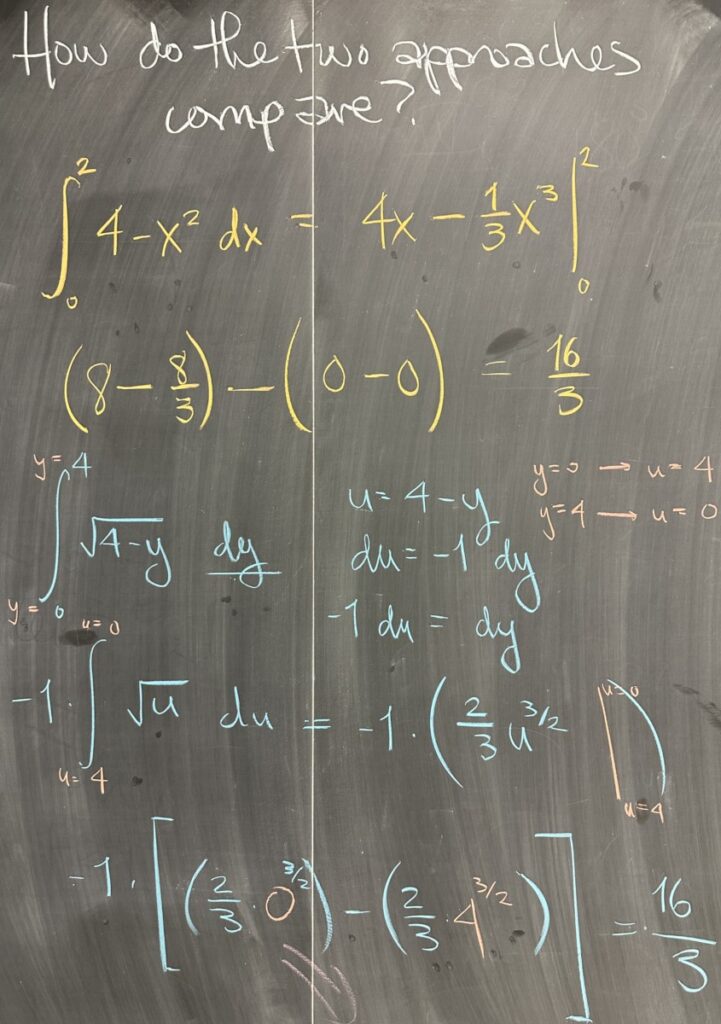
Since both strategies are computing the area of the same region, it is expected that both integrals result in the same value.
The “dx” integral is straightforward: apply the power rule to find the antiderivative of \(4-x^2\,dx\), then subtract its evaluation at \(x=0\) from the same at \(x=2\). \[4x-\frac{1}{3}x^3\Bigg\vert_0^2 = \left(8-\frac{8}{3}\right)-0 = \frac{16}{3}\]
The “dy” integral requires more attention. In order to find the antiderivative of \(\sqrt{4-y}\,dy\), we need to use u-substitution with \(u = 4-y\) and \(du = – \,dy\). After the substitution, we are left to find the antiderivative \(- \int\sqrt{u}\,du = – \frac{2}{3}u^\frac{3}{2}\).
Converting our \(y\) bounds to \(u\) bounds, we get \[\int_4^0 \sqrt{u}\,du = – \frac{2}{3}u^\frac{3}{2} \Bigg\vert_4^0 = \frac{16}{3}\]
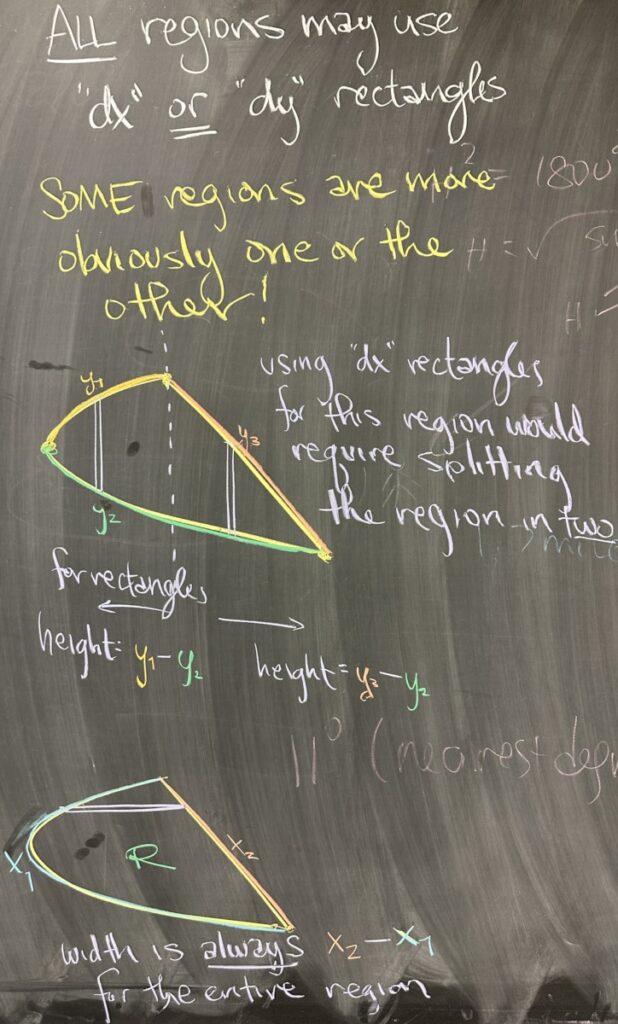
It is important to keep in mind that every region can be “sliced” using either “dx” or “dy” rectangles. It should also be clear that both ways are measuring the same area and should have the same value. But just because both options will work out to the same final value does not mean that both will options will have similar difficulty.
As evidence of the big difference that can arise between the two options, consider a horizontally oriented parabola (opening to the right) intersected by a line with negative slope. If we attempt to compute the area of this region using vertical “dx” rectangles, we encounter the following issue: the region does not have a consistent “upper” boundary. Rather, the region has two different “upper boundaries. On the left side of the region, the upper boundary is the top half of the parabola; and on the right side of the region, the upper boundary is the line.
In this situation, where there are two different curves that form the upper (or lower) boundary, there are two different height functions for the region: one for the side bounded by the parabola, and another for the side bounded by the line. As a result, the “dx” rectangle strategy will require two separate integrals to cover the region.
On the other hand, if we consider the same region with horizontal “dy” rectangles, we do not need “upper” and “lower” bounds for the region — instead, we need “left” and “right” bounds. This region is consistently bounded on the left by the parabola and bounded on the right by the line. There will be a consistent “width” function for the region, and no need for two separate integrals when using the “dy” strategy.
Having this understanding of both strategies will help you deal with the regions appearing in the next section: Volumes of Solids of Revolution.
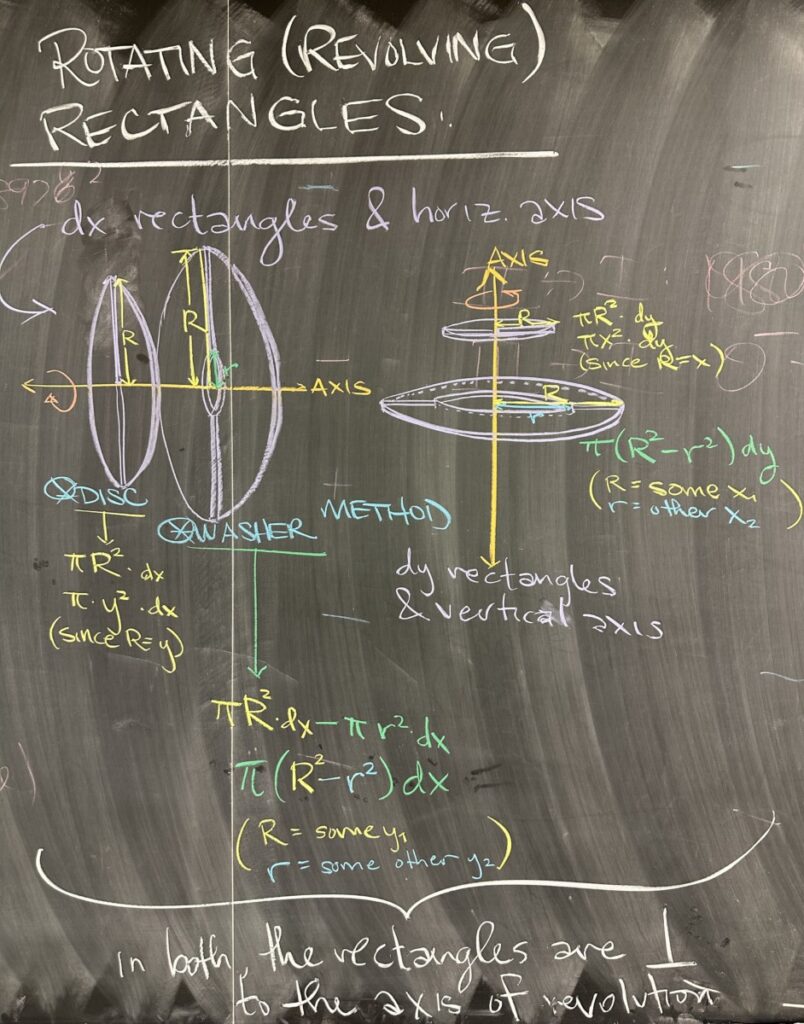
First up, we consider rotating vertical “dx” rectangles around a horizontal axis. If the region shares a boundary with the axis of revolution, the rectangle will revolve to make a “disc” shape (like a coin).
If we instead consider rotating horizontal “dy” rectangles around a vertical axis, the same disc shape is created. In both cases, the similarity in resulting shape is due to the fact that our rectangles are perpendicular to the axis of revolution.
Remember that our differentials (“dx” or “dy”) are infinitesimally small just as the rectangles in our Riemann Sums became infinitesimally narrow as we approached an infinite number of rectangles. Because the disc is so thin, we essentially only consider the area of the circle.
Imagine that the disc is as thin as a piece of paper. If you received a circular piece of paper, it would be more reasonable to consider its area rather than its volume. The area of a circle with radius \(R\) is \(\pi R^2\), and its volume as a disc would be \(\pi R^2 \, dx\) or \(\pi R^2 \, dy\).
If our region does not share a boundary with the axis of revolution, there will be “empty space” between the rectangle and the axis — causing a hole to appear in the disc that is created when the rectangle is revolved around the axis. Rather than calling this shape a “disc”, the term “washer” is used instead. Both “disc” and “washer” often appear together in reference to the shape created by revolving these rectangles that are perpendicular to their axis of revolution.
If we again consider the area for this “washer” shape, it is a circle with a circular hole in the center — meaning that its area will be that of the inner circle subtracted from the outer circle. If the outer circle has radius \(R\) and the inner circle has radius \(r\), the total area would be \[\pi R^2-\pi r^2 = \pi\left(R^2-r^2\right)\]
Multiplying the area by the differential (the “thickness” of the washer), we get the volume: \[\pi\left(R^2-r^2\right)\, dx \text{ or } \pi\left(R^2-r^2\right)\,dy\]
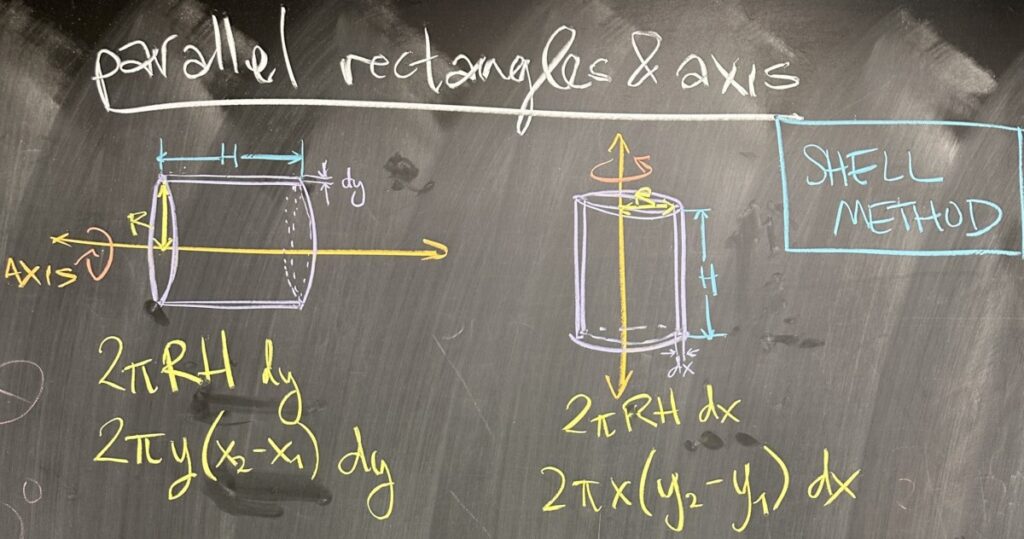
The remaining two combinations of rectangles and axis are both oriented in parallel instead of being perpendicular. One combination is a horizontal “dy” rectangle with a horizontal axis of revolution, and the other is a vertical “dx” rectangle with a vertical axis of revolution.
In both cases, a “tube” shape is created — but the standard terminology for this situation is the “shell” method.
Similar to the disc/washer method, we first consider the area of the created shape because the differential (“dx” or “dy”) is infinitesimal. In other words, our tube will be microscopically thin.
In thinking about the area for such a tube, imagine the leftover tube at the center of a roll of paper towels. If this tube is cut along its length and laid flat, it would form a rectangle. One side of that rectangle would be the length of the tube, while the other side originally formed the circumference of the circular end of the tube. If the radius of the tube is \(R\) and the length of the tube is \(H\), then the area of the tube is \(2\pi R \cdot H\), and as a volume: \(2\pi R \cdot H \cdot dx\) or \(2\pi R \cdot H \cdot dy\).
The measurement for \(R\) and \(H\) will depend on the region and the orientation (either “dx” or “dy” rectangles). In the “dx” case, the radius \(R\) is measured in the \(x\)-direction (distance from \(x\) to the axis) while the length \(H\) is measured in the \(y\)-direction. In the “dy” case, everything is reversed: \(R\) is in the \(y\)-direction and \(H\) is in the \(x\)-direction.
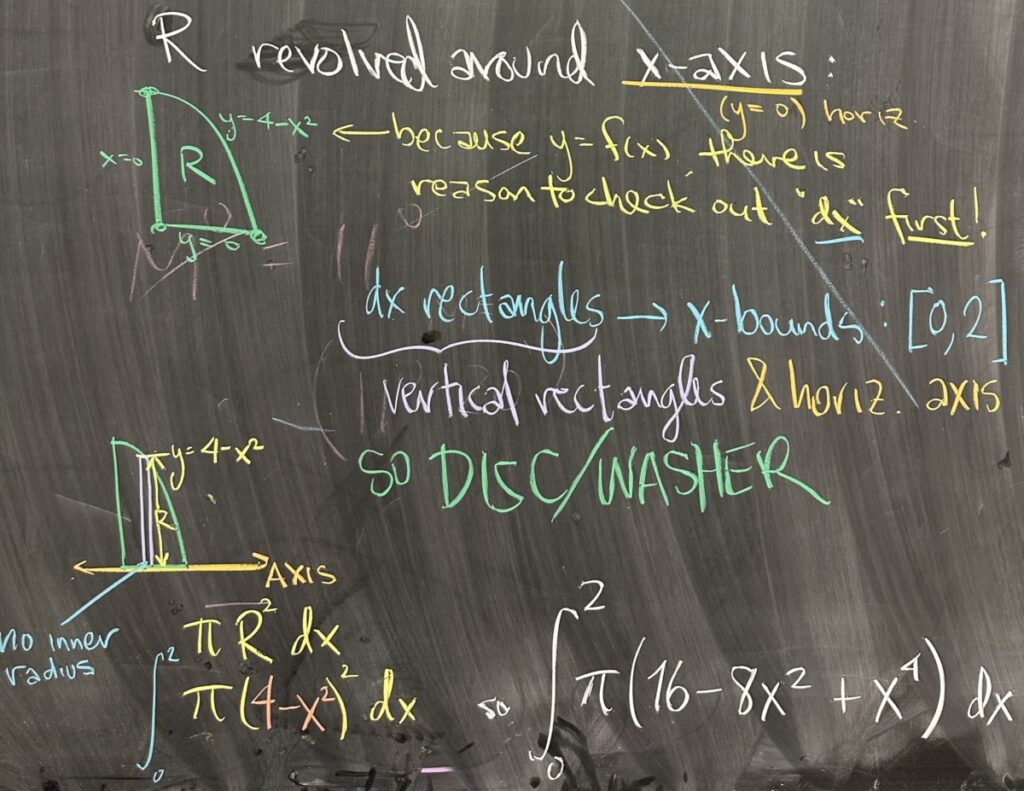
Returning the region which we defined at the start of the lesson, we now consider revolving this region around the \(x\)-axis (\(y=0\)). Since our region was originally given by the equation \(y = 4-x^2\) (with \(x\) as the independent variable), it is reasonable to start by trying to use “dx” rectangles.
Using “dx” rectangles means that we need an interval for \(x\), and we know that for our region, all \(x\)-values come from the interval \([0,2]\).
Furthermore, using “dx” rectangles with a horizontal axis (\(y=0\)), we know that this will create discs or washers. Since \(y=0\) is a boundary for our region and the axis of revolution, we know that revolution will create discs and not washers (inner radius is zero).
Using our formula \(\pi R^2\,dx\), we must determine the radius \(R\) for our region. \(R\) is given by the distance from the \(y\)-value on the parabola \(y=4-x^2\) to the \(x\)-axis \(y=0\). Because we are using “dx” rectangles (hence \(x\) is our independent variable), we want to express this difference in terms of \(x\): \(R = (4-x^2)-(0)\).
Putting everything together, our volume integral is: \[\int_a^b \pi R^2\,dx = \int_0^2 \pi \left(4-x^2\right)^2\,dx\]
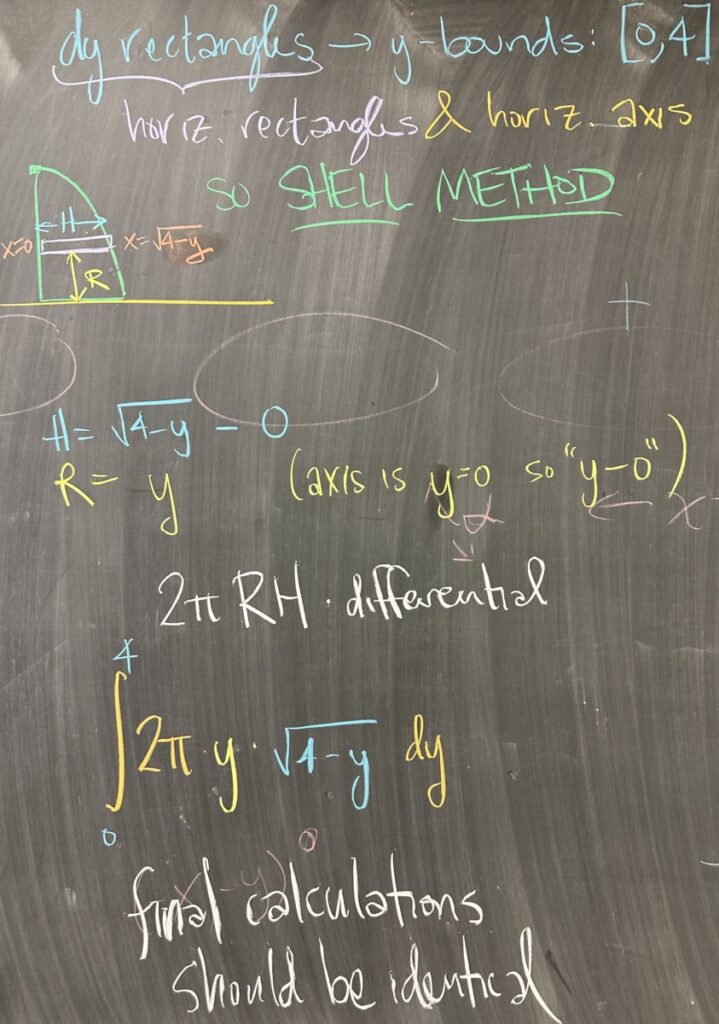
If we consider the same calculation (revolving the region around the \(x\)-axis) using “dy” rectangles instead, we must start with the interval for \(y\): \([0,4]\). Then we compare the orientation of the “dy” rectangles (horizontal) to the axis of revolution (also horizontal) and conclude that this will require the “shell” method.
For the shell method, we must determine the radius and length/height of the “tube” that will be formed by revolving a “dy” rectangle around \(y=0\). Radius is always measured perpendicular to the axis of revolution — in this case, it is a difference of \(y\)-values.
Since we are using “dy” rectangles, this also means that \(y\) is our independent variable instead of \(x\). Because of this, we must express both \(R\) and \(H\) in terms of \(y\). For \(R\), we again need a difference of \(y\)-values, this time in terms of \(y\): \(R = y-0\).
For \(H\), we must measure in parallel to the axis of revolution. Our rectangle will be determined by the \(x\)-value on the left of the region, \(x = \sqrt{4-y}\) and the \(x\)-value on the right of the region, \(x = 0\). \(H\) is the difference between these two values: \(H = \sqrt{4-y}-0\) (again, note that this is expressed in terms of \(y\)).
Putting everything together, our volume integral looks as follows: \[\int_a^b 2\pi R H \,dy = \int_0^4 2\pi y \sqrt{4-y}\,dy\]
These first two integrals compute the volume of the same region revolved around the same axis, and should therefore result in the same value. Compute them yourself to confirm this fact! \[\int_0^2 \pi \left(4-x^2\right)^2\,dx = \int_0^4 2\pi y \sqrt{4-y}\,dy\]
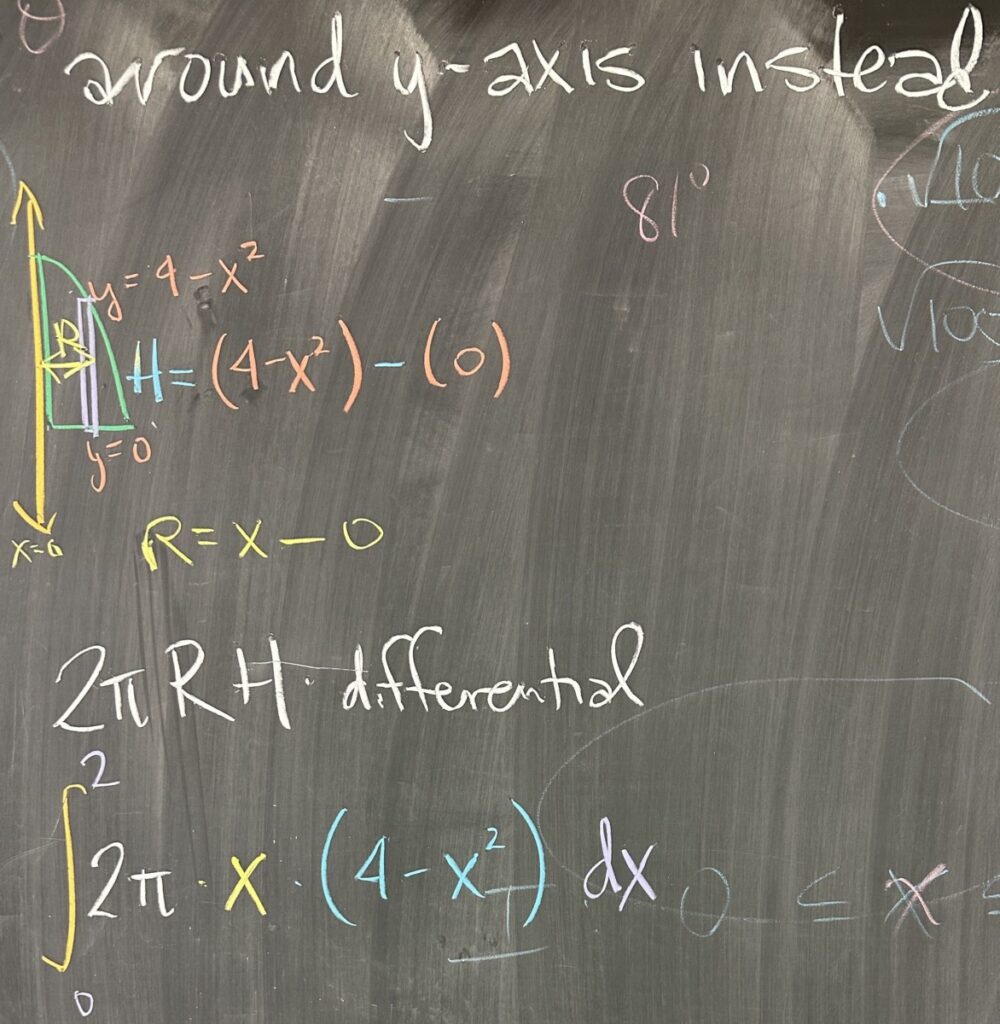
Again, considering the same region — but this time revolving around the \(y\)-axis (\(x=0\)). If we first slice our region using “dx” rectangles, we have \(x\) as our independent variables, and will again use \([0,2]\) as our interval for \(x\)-values.
Since our vertical “dx” rectangles are parallel to the axis of revolution \(x=0\), that means this computation will use “shell” method. For the shell method, we must find both \(R\) and \(H\). Since \(R\) is measured in the \(x\) direction and our independent variable is also \(x\), we have that \(R\) is the difference between \(x\) and our \(x=0\) axis: \(R = x-0\).
Since \(H\) is measured in the \(y\) direction, we will need to subtract the lower \(y\)-bound (\(y=0\)) from the upper \(y\)-bound (\(y=4-x^2\)): \(H = (4-x^2)-0\). Again, note that we are required to express both \(R\) and \(H\) in terms of our independent variable, \(x\).
Putting it all together: \[\int_a^b 2\pi R H \, dx = \int_0^2 2\pi x (4-x^2)\,dx\]
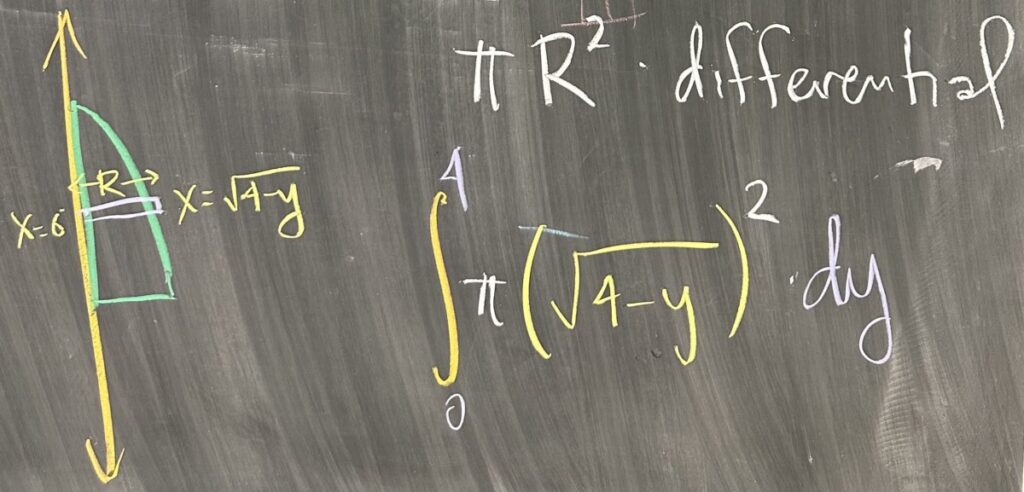
If we then switch to the horizontal “dy” rectangles, we need to use \(y\) as our independent variable with interval \([0,4]\) for our \(y\)-values. Because our “dy” rectangles are perpendicular to the axis of revolution, this computation will use the “disc/washer” method. \(R\) is measured in the \(x\) direction as the difference between the parabola \(x=\sqrt{4-y}\) on the right and the axis \(x=0\) on the left: \(R = \sqrt{4-y}-0\).
Putting it all together: \[\int_a^b \pi R^2\,dy = \int_0^4 \pi \left(\sqrt{4-y}\right)^2\,dy\]
Once again, with these two examples representing the same region revolved around the same axis, we expect that the result of the two definite integrals are equal: \[\int_0^2 2\pi x (4-x^2)\,dx = \int_0^4 \pi \left(\sqrt{4-y}\right)^2\,dy\]
Do they end up equal? Compute both and find out!



Recent Comments