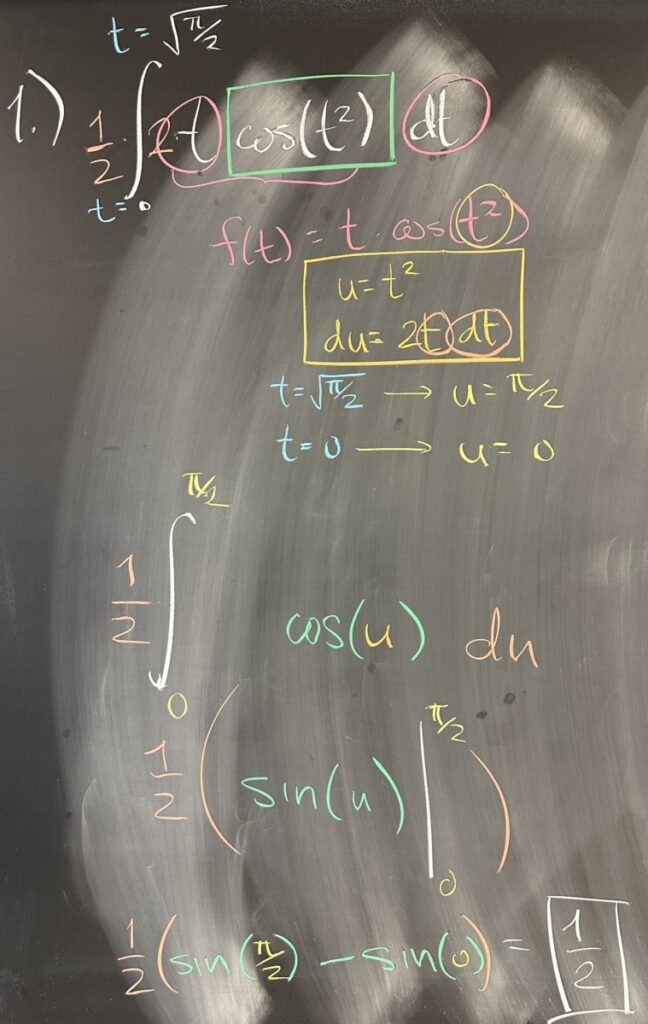
Today’s first quiz problem is a definite integral. It is important to consider what our final result should look like — in this case, as a definite integral, our result should be a real number (representing the area bounded by \(f(x)\), the \(x\)-bounds, and the \(x\)-axis).
Looking at just the \(\cos(t^2)\) factor of our function, we should recognize that this is a composition of functions: \(\cos(u)\) with \(u = t^2\). With this as our substitution, we then find \(du = 2t\, dt\). However, the remaining factor of our function is \(t\, dt\). This is close to what we need for \(du\), except for \(2\). We have several options for resolving this, such as \(\frac{1}{2} \, du = t\, dt\).
After substituting, we have \(\int \cos(u) \frac{1}{2} \, du\). However, we must still consider our bounds, since this problem started out as a definite integral. When we convert \(t^2\) to \(u\), we must also convert \(t = \sqrt{\frac{\pi}{2}}\) to \(u = \left(\sqrt{\frac{\pi}{2}}\right)^2 = \frac{pi}{2}\), and also \(t = 0\) to \(u = 0^2 = 0\).
At this point, we must pause and consider our new integral — asking ourselves, did we successfully remove all traces of the original variable, \(t\)? The answer here is yes, so we conclude that our substitution is successful.
Now, all that remains is to find an antiderivative of \(\frac{1}{2}\cos(u)\), \(\int \frac{1}{2}\cos(u)\,du = \frac{1}{2}\sin(u)\), and then evaluate at the \(u\)-bounds: \(\frac{1}{2}\sin\left(\frac{\pi}{2}\right) – \frac{1}{2}\sin(0) = \frac{1}{2}\).
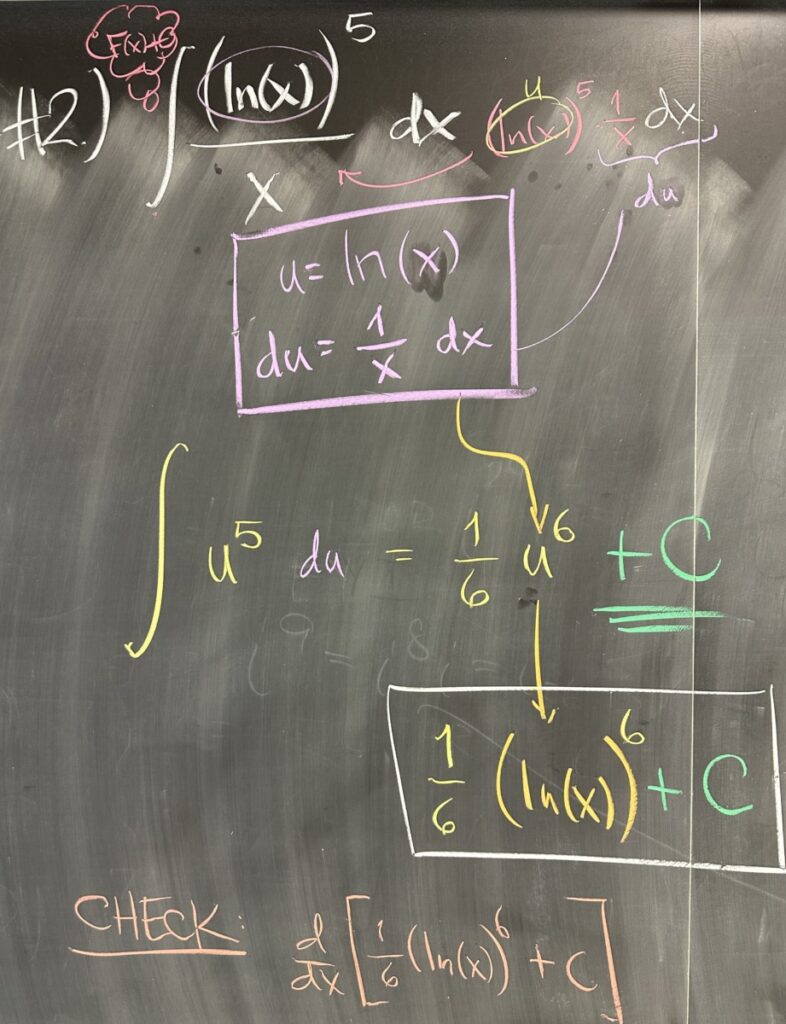
In the second quiz problem, we again recognize that one of our factors is a composition of functions: \((\ln(x))^5 = u^5\) with \(u = \ln(x)\). With this substitution, we then find \(du = \frac{1}{x}\,dx\). This looks good for us, because the remaining factor of the original function is also \(\frac{1}{x}\,dx\).
As an indefinite integral, our problem should have a solution that is a function of \(x\), and should also include the unknown vertical shift: \(+C\).
So we find an antiderivative of \(u^5\), which is \(\frac{1}{6}u^6 + C\). We cannot hang on to \(u\) as the variable for our antiderivative, so we convert back to \(x\) with a final result: \(\frac{1}{6}\left(\ln(x)\right)^6 + C\).
Keep in mind, that with all indefinite integrals, the derivative of our answer should simplify to give our original function.
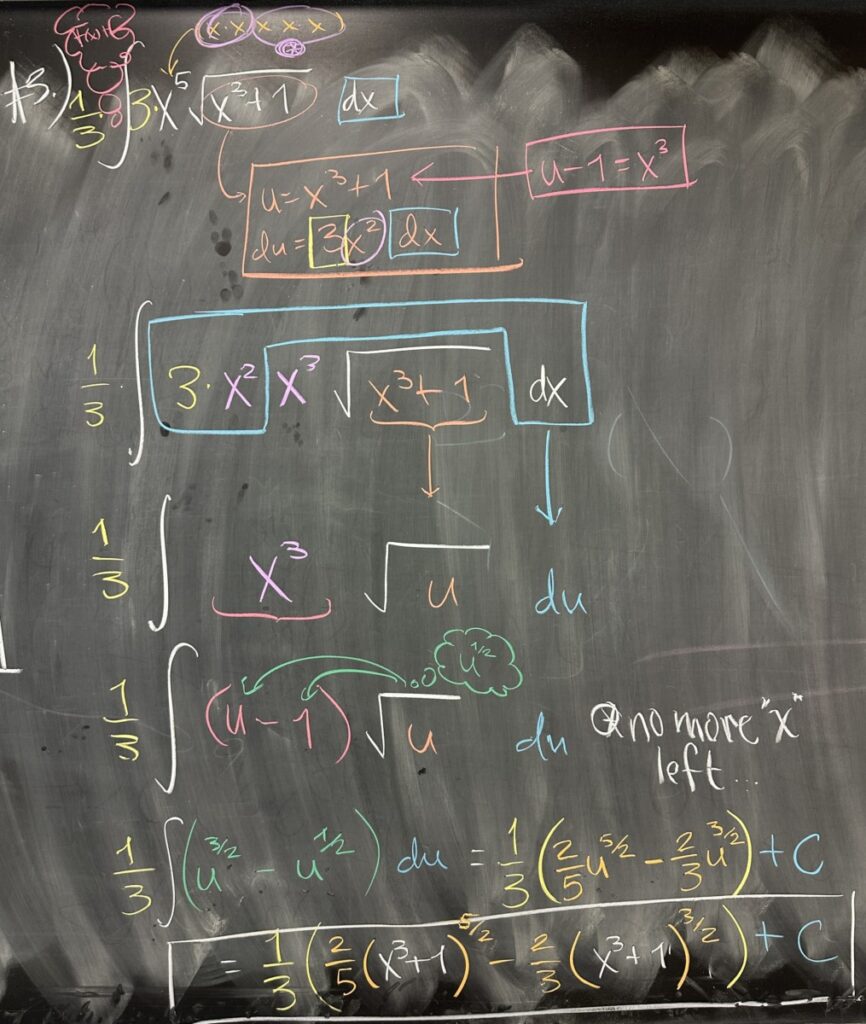
In the final quiz problem, we again identify a factor that is a composition of functions: \(\sqrt{x^3+1} = \sqrt{u}\) with \(u = x^3+1\). As with the previous problems, we find that \(du = 3x^2\,dx\) — but this is not as clear of a match for our remaining factor: \(x^5\,dx\).
We can split \(x^5\) since we want \(x^2\) for the \(du\) substitution. So our remaining factor can be written as \(x^3 x^2\, dx\) and we have \(du = 3x^2\,dx\) which we can rewrite as \(\frac{1}{3}\,du=x^2\,dx\).
This means our remaining factor, \(x^5\,dx\), can be substituted: \(x^5\,dx = x^3 x^2\,dx = x^3 \frac{1}{3}\,du\). The problem here is that our overall integral now looks like: \[\int x^5\sqrt{x^3 + 1}\,dx = \int x^3 \sqrt{u} \frac{1}{3}\,du\]
This substitution is incomplete because we have \(x\) mixed together with \(u\) and \(du\). In order to finish the substitution, we need to find a way to substitute \(x^3\). This is possible because \(u = x^3 + 1\), which is equivalent to saying \(u – 1 = x^3\). With this perspective, we are able to finish the substitution: \[\int x^3 \sqrt{u} \frac{1}{3} \,du = \int (u – 1)\sqrt{u} \frac{1}{3} \, du = \frac{1}{3} \int (u-1) \sqrt{u} \, du\]
All that remains is to find the antiderivative of \((u-1)\sqrt{u}\). Since we only know basic antiderivatives, this product will need to be rearranged in a manner that allows us to take antiderivatives of “basic” functions. In this case, consider \(\sqrt{u}\) as \(u^\frac{1}{2}\) and then distribute the product to the binomial \(u – 1\): \[\frac{1}{3} \int (u-1)\sqrt{u}\,du = \frac{1}{3} \int u^\frac{3}{2} – u^\frac{1}{2}\,du\]
Now we can apply the power rule for antiderivatives and find our final answer: \[\frac{1}{3} \int u^\frac{3}{2} – u^\frac{1}{2}\,du = \frac{1}{3}\left(\frac{2}{5}u^\frac{5}{2} – \frac{2}{3}u^\frac{3}{2}\right)+C\]
After replacing \(u\) with \(x^3+1\), we end up with the antiderivative in terms of our original variable, \(x\): \[\frac{1}{3}\left(\frac{2}{5}(x^3+1)^\frac{5}{2} – \frac{2}{3}(x^3+1)^\frac{3}{2}\right) + C\]
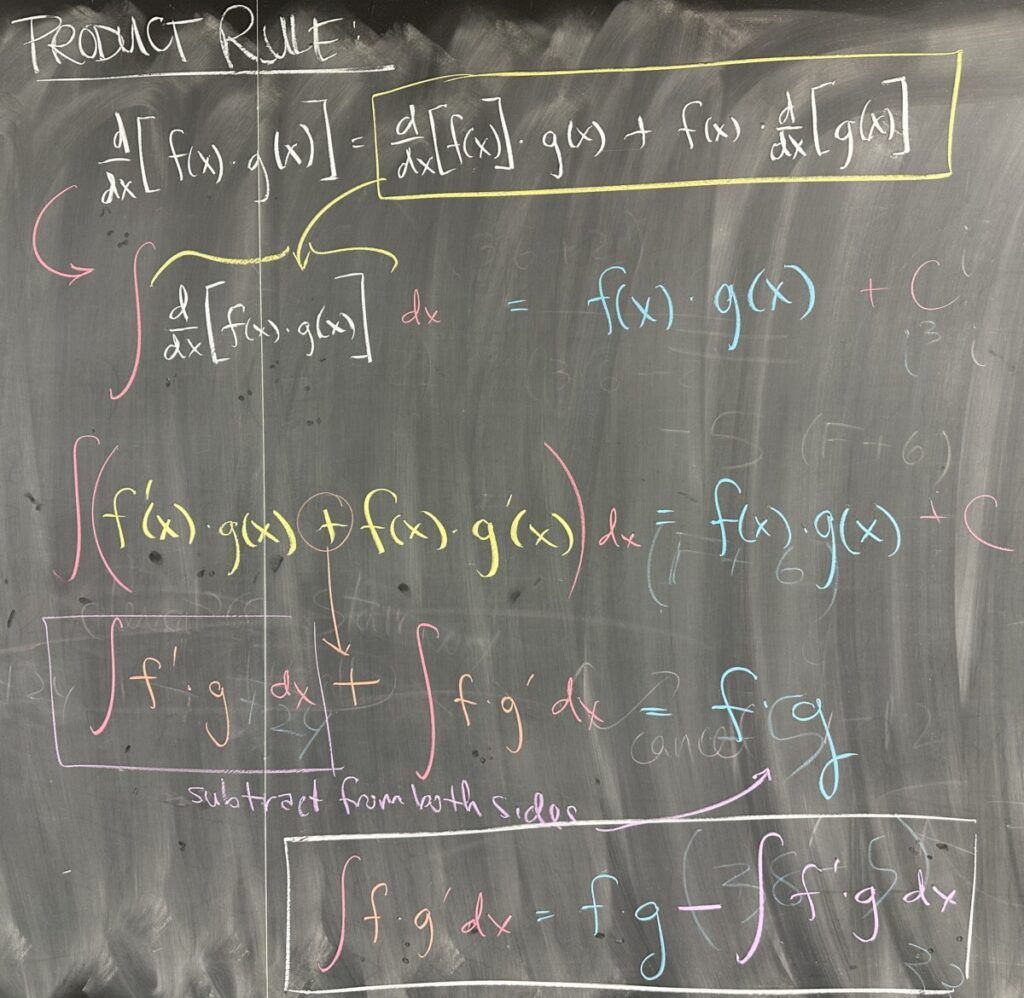
Today’s lesson covers the antiderivative version of the product rule for derivatives. Starting with the product rule and the notion that the antiderivative of a derivative of a function is (more or less) back to the original function.
Using this interpretation of the product rule, we end up finding that: \[\int f \cdot g’ \, dx = f \cdot g – \int f’ \cdot g\, dx\]
For convenience, we write this slightly differently:
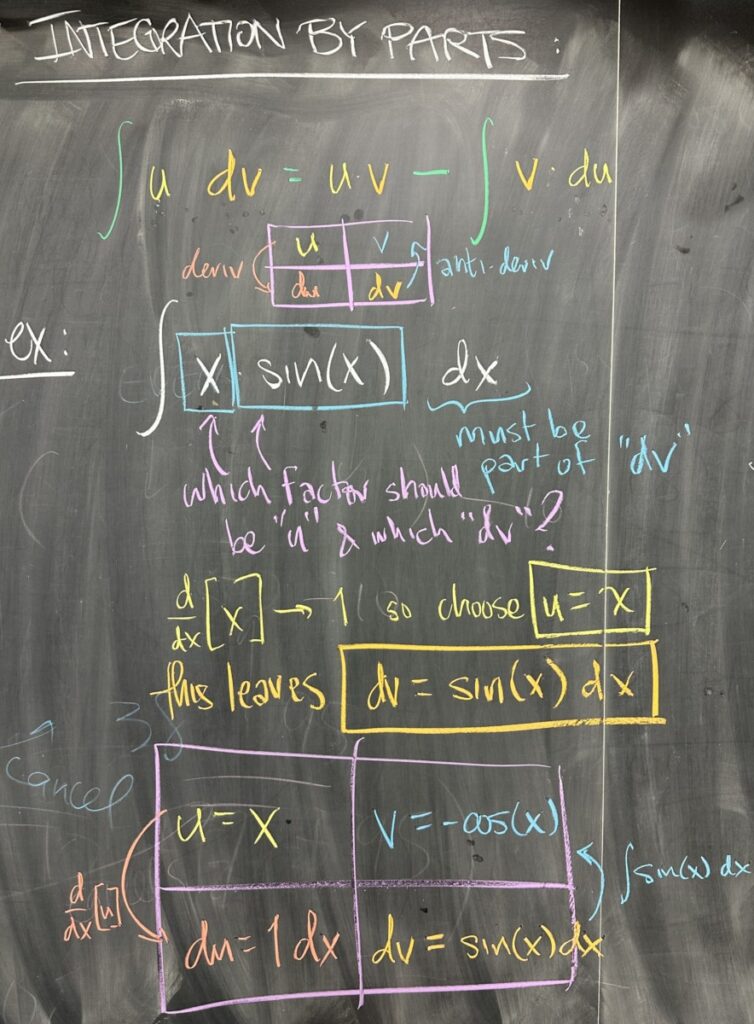
“Integration by Parts” is the name given to the antiderivative version of the product rule. Instead of using \(f\), \(f’\), \(g\), and \(g’\), we will use \(u\), \(du\), \(v\), and \(dv\).
In practice, we start with the integral of a product: \(\int u \, dv\), splitting the function into factors and assigning those factors to either \(u\) or \(dv\). In order to continue with Integration by Parts, we must find \(du\) from \(u\) and find \(v\) from \(dv\).
Note that finding \(du\) requires the derivative of \(u\), and \(v\) requires the antiderivative of \(dv\). I recommend using a 2×2 grid to keep this work organized. Another recommendation is to choose \(u\) to be factors whose derivative is simpler than \(u\) — and choose \(dv\) to be factors whose antiderivative will not get more complicated than \(dv\).
Once we complete our grid, we have all four components that we need to rewrite our original integral: \[\int u\,dv = uv – \int v\,du\]
Looking at an example: \(\int x\sin(x)\,dx\), we have three factors: \(x\), \(\sin(x)\), and \(dx\). \(dx\) must be part of \(dv\), so either \(u = x\) or \(u = \sin(x)\) — the better of which is \(u = x\) since that would make \(du = dx\). That leaves \(dv = \sin(x)\,dx\), which has antiderivative \(v = -\cos(x)\).
Using Integration by Parts, now: \[\int (x)(\sin(x)\,dx) = (x)(-\cos(x)) – \int (-\cos(x))(dx) = -x\cos(x) + \int \cos(x)\,dx\]
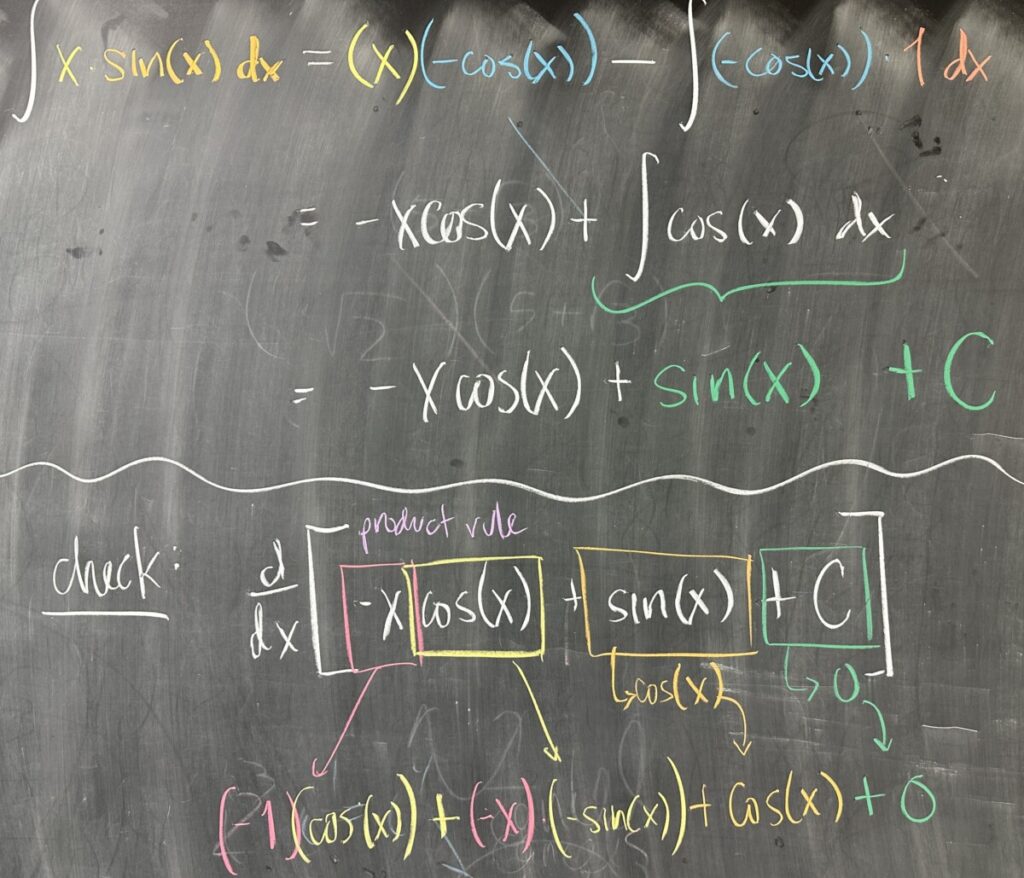
This is easier to carry out, since we actually know \(\int \cos(x)\,dx = \sin(x)\). With this in mind: \[-x\cos(x) + \int \cos(x)\,dx = -x\cos(x) + \sin(x) + C\]
When we come to this result, we can check our work by taking the derivative and confirming that the result is our original \(x\sin(x)\). What we should notice is that our \(uv = -x\cos(x)\) requires the product rule, which is a sum of two terms, but then the derivative of our \(\int v\,du = \sin(x)\) actually cancels out one of the terms coming from the product rule on \(uv\). The final result does, in fact, match the original \(x\sin(x)\).
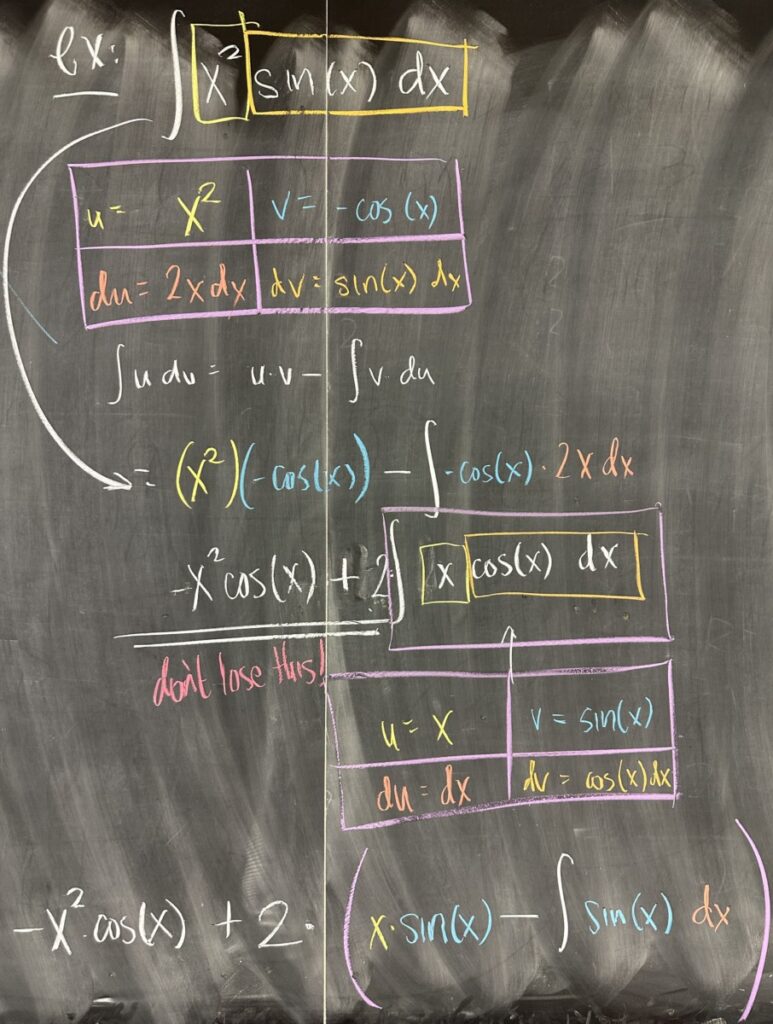
The next example is a modified version of the previous example. In this case, we have \(x^2\) instead of \(x\) as a factor with \(\sin(x)\).
In this case, we must use integration by parts twice! The first time, we choose \(u=x^2\), which gives \(du = 2x\,dx\). In the second application of integration by parts, we choose \(u = x\), which gives \(du = dx\).
Notice that in each case, we use the 2×2 grid to organize our parts before applying Integration by Parts. The final result is the sum of three terms, two of which are products (i.e. their derivatives would require the product rule). Also, don’t forget that, as an indefinite integral, our answer is an antiderivative family that includes “+C”!
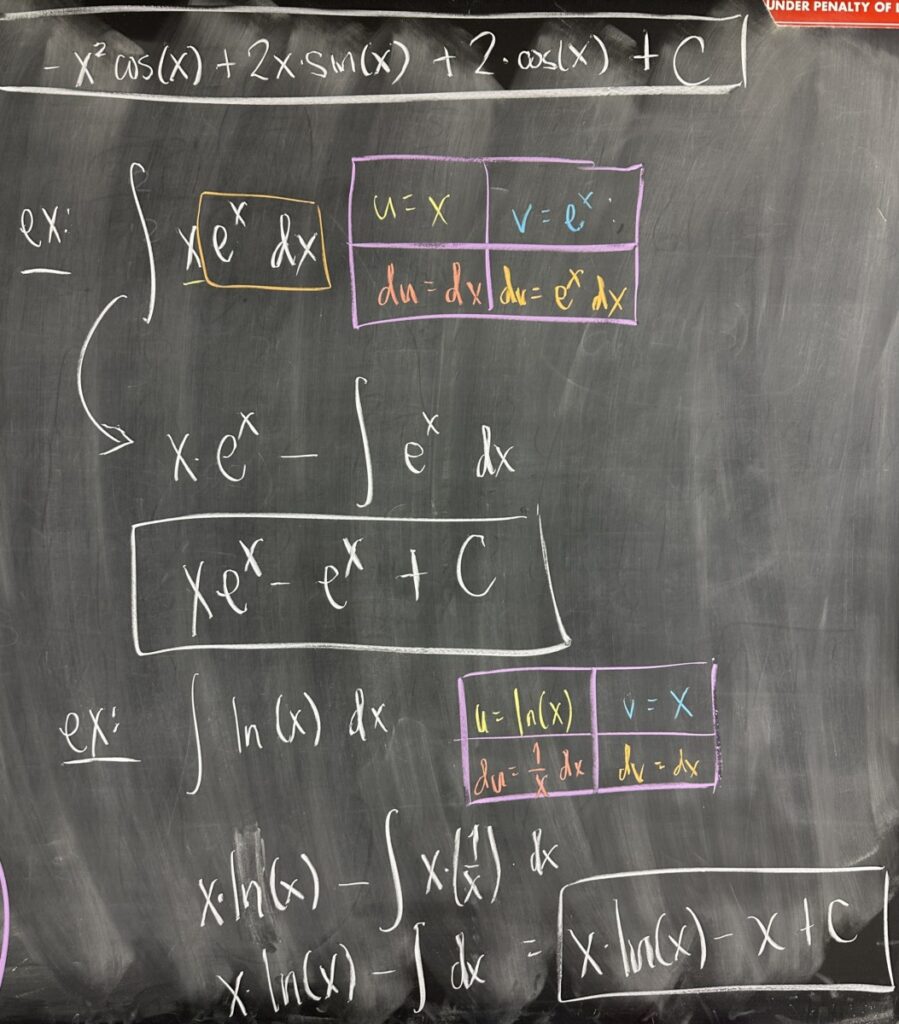
We ended the class with two quick examples, \(\int x e^x\,dx\), which works out very similarly to our \(\int x \sin(x)\,dx\); and \(\int \ln(x)\,dx\), which is very different!
In the latter case, we don’t even seem to have a case where the product rule would even apply! However, we have a fundamental issue in that we don’t know of ANY function whose derivative is \(\ln(x)\) — but we DO know the derivative of \(\ln(x)\). Unfortunately, our indefinite integral is the antiderivative and not the derivative… but Integration by Parts is here to help us out. By choosing \(u = \ln(x)\) and leaving \(dv = dx\) (the only factor remaining), we end up with an antiderivative that we can find: \[x \ln(x) – \int x \left(\frac{1}{x}\right)\,dx = x \ln(x) – \int \,dx = x \ln(x) – x + C\]



Recent Comments