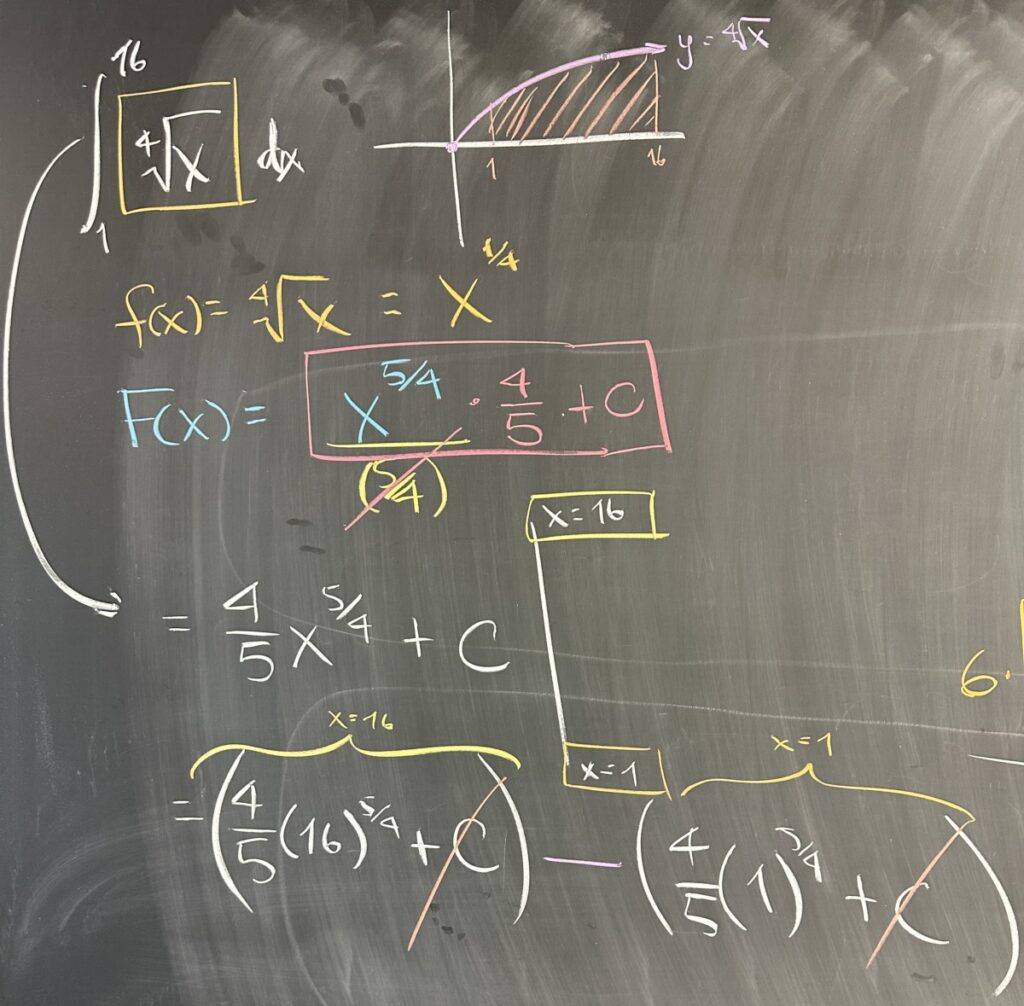
The first quiz problem is a definite integral. We started by thinking about what the function \(f(x) = \sqrt[4]{x}\) looks like when graphed, with the bounds \(x=1\) and \(x=16\). This region is not a “nice” geometric shape — so computing the area will require the Fundamental Theorem of Calculus.
Taking the antiderivative of \(\sqrt[4]{x}\) will require a shift in the way we represent it algebraically. In order to apply the power rule for antiderivatives, we need to represent \(\sqrt[4]{x}\) as a power of x: \(x^\frac{1}{4}\).
Then the power rule (with \(p = \frac{1}{4} \)): \[\int x^p \, dx = \frac{1}{p+1} x^{p+1} + C\]
With our antiderivative in hand, \(F(x) = \frac{4}{5}x^\frac{5}{4}\), we can then evaluate at \(x=1\) and \(x=16\) and then subtract. Notice that the usual “+C” on our antiderivative is irrelevant in this (and any) definite integral problem — the subtraction will always create \(C – C\) which is zero.
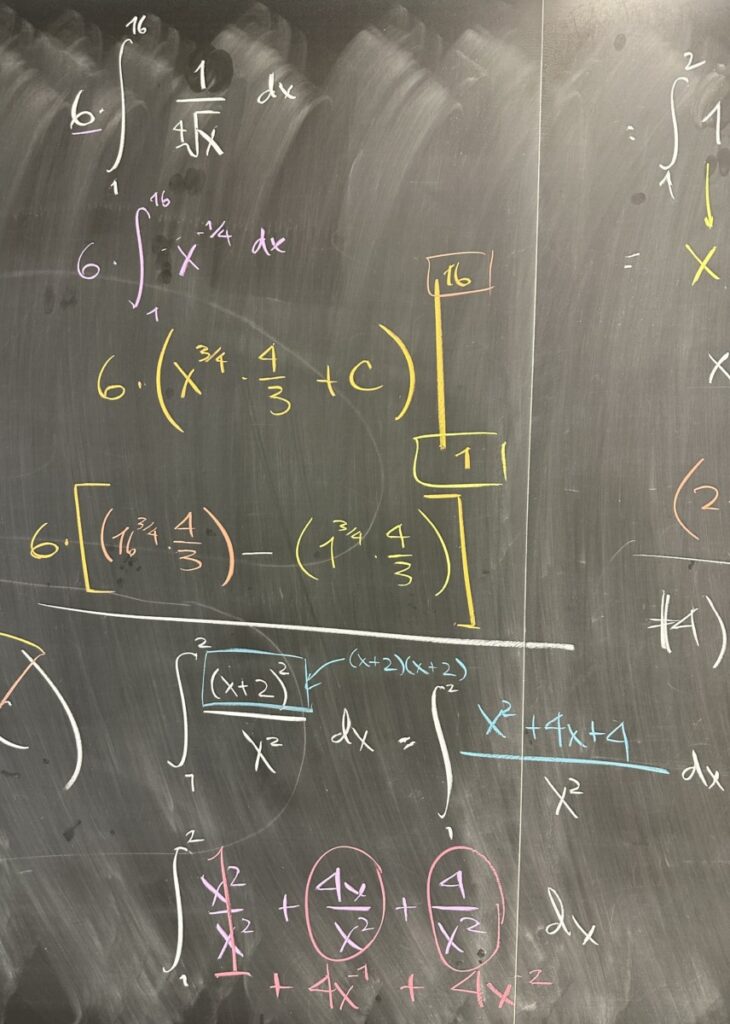
In the second quiz problem, we have a similar situation as the first, where we want to think of our function as a power of \(x\) rather than as a radical. \[\frac{6}{\sqrt[4]{x}} = 6x^\frac{1}{4}\]
And further, we factor the coefficient of \(6\) outside of the integral. This means that we will first find the area bounded by \(x^\frac{1}{4}\) and then multiply by six — instead of directly finding the area bounded by \(6x^\frac{1}{4}\).
After applying the power rule for antiderivatives, we find that \(F(x) = \frac{4}{3}x^\frac{3}{4}\). Finally, we substitute our bounds: \(x =1\) and \(x = 16\), and then subtract to get our final answer for the area of the region described by this definite integral.
The third quiz problem required a different kind of reconfiguration. Instead of radicals being rewritten as powers, we have a power of a binomial that would be easier to work with when written as an expanded polynomial.
After multiplying out \((x+2)(x+2)\), we then distribute the division by \(x^2\) and simplify to see that our original function \(f(x) = \frac{(x+2)^2}{x^2}\) is identical to (the easier to work with) \(f(x) = 1 + 4x^{-1} + 4x^{-2}\).
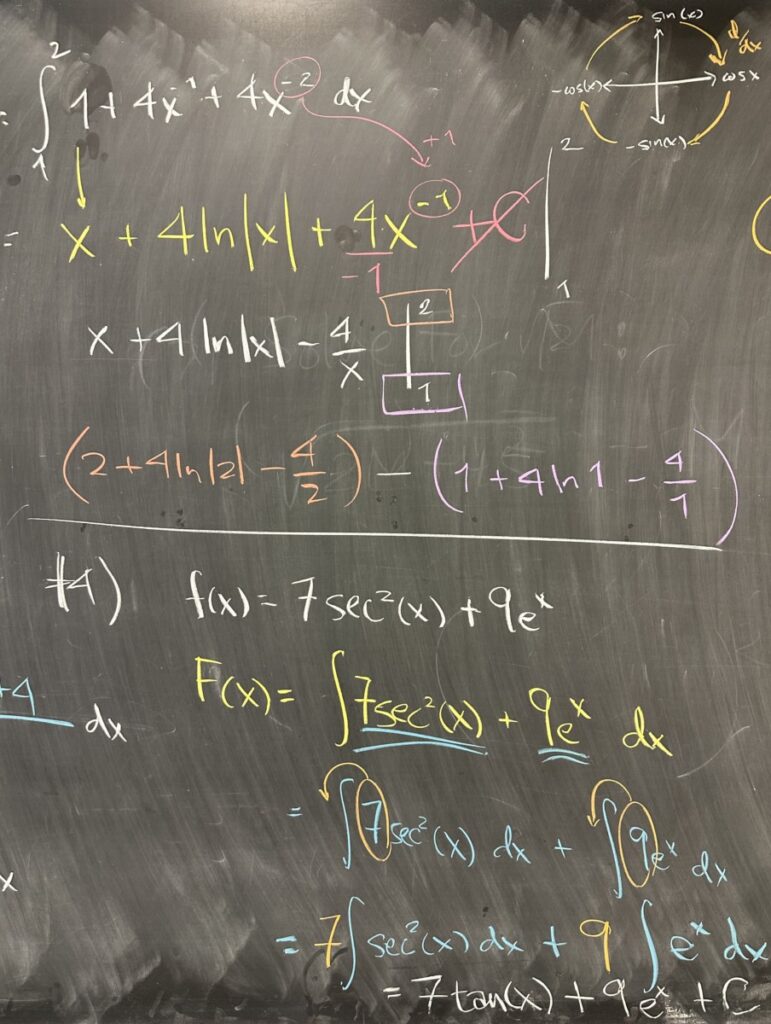
The form \(1 + 4x^{-1} + 4x^{-2}\) is preferred because the power rule for antiderivatives is easy to apply. However, we must be careful! The power rule for antiderivatives works for all powers except for \(x^{-1}\).
So, our antiderivative ends up being \(F(x) = x + 4\ln(|x|) – 4x^{-1} + C\), though we again are in the midst of a definite integral problem, so the “+C” is not going to be relevant. I keep pointing out the need for “+C” when finding antiderivatives because it is something that everyone needs to think about every time, not just when we think we need it.
The final steps are to evaluate our antiderivative at the bounds and subtract: \(F(2) – F(1)\).
Problem 4 on the quiz asked for the most general form of the antiderivative — so “+C” is definitely relevant here! We split up the function into constant multiples of “smaller” integrals, and found the antiderivative of each term separately. \(\int \sec^2(x)\,dx = \tan(x)\) and \(\int e^x\,dx = e^x\).

For the final quiz problem, we were given that \(f(0) = 4\) and the derivative of \(f\) is \(f'(x) = 7\sin(x)\). So we know that \(f\) is the antiderivative of \(f’\), and from the family of antiderivatives, there will be only one that satisfies \(f(0)=4\).
The antiderivative of \(7\sin(x)\) is \(7\) times the antiderivative of \(\sin(x)\), so we have that \(f(x)\) is from the family: \(-7\sin(x) + C\).
The specific function for \(f\) can be determined by using \(x = 0\) and \(f(0) = 4\). Using the family of antiderivatives, we can evaluate them all at \(x=0\): \(-7\cos(0) + C = -7 + C\), which could be any number (depending on what value is used for \(C\)). But only one of them will be \(4\): \[-7 + C = 4 \longrightarrow C = 11\]
So we know that \(f(x) = -7\cos(x) + 11\) is the only function in the antiderivative family that satisfies the initial conditions. We can (and should) check our work to make sure that \(f(0)\) and \(f’\) are what they should be.
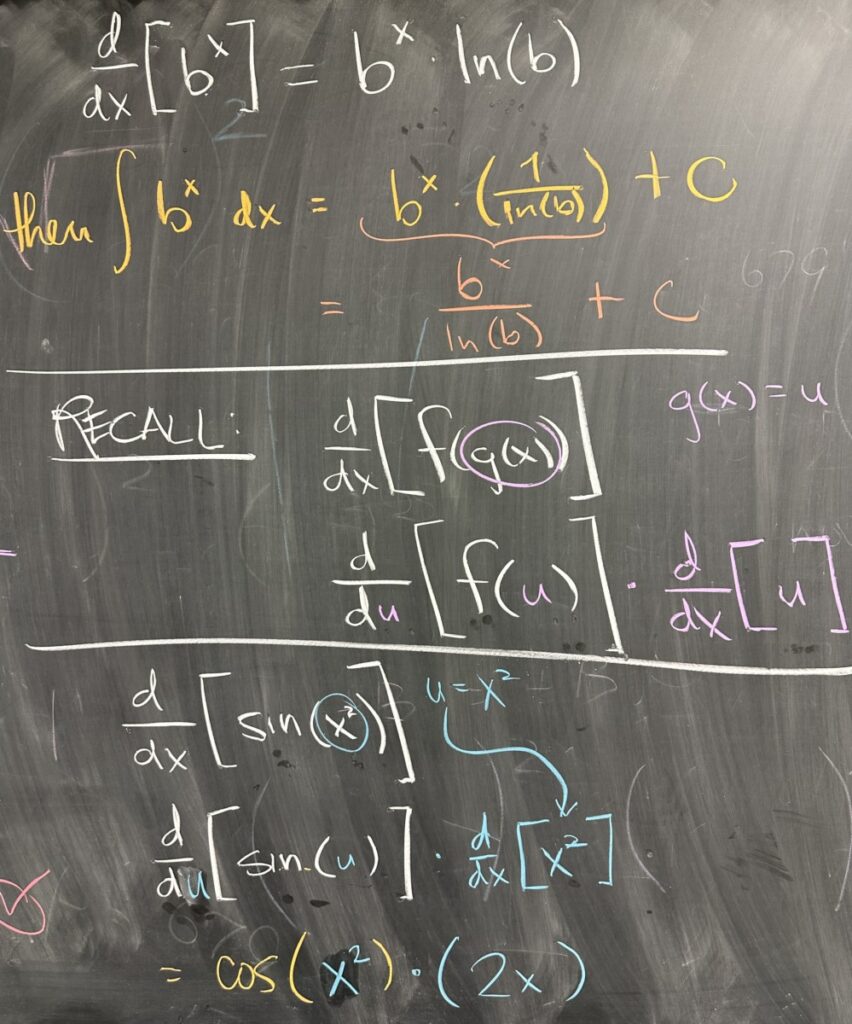
After the quiz we discussed how to find antiderivatives of exponential functions (with any base, not just \(e\)). Since the derivative of an exponential function follows a very specific pattern: \[\frac{d}{dx}\left[b^x\right] = b^x \ln(b)\]
We can infer that the antiderivative does the opposite: \[\int b^x\,dx = \frac{b^x}{\ln(b)} + C\]
Instead of multiplying a factor of \(\ln(b)\), as we do when taking the derivative, the antiderivative divides a factor of \(\ln(b)\).
We then quickly reviewed the chain rule for derivatives. I like to think of the chain rule as a substitution, making a “chain” of simple derivatives with respect to substituted variables: \[\frac{d}{dx}\left[\sin(x^2)\right] = \frac{d}{du}\left[\sin(u)\right] \cdot \frac{d}{dx}\left[x^2\right]\]
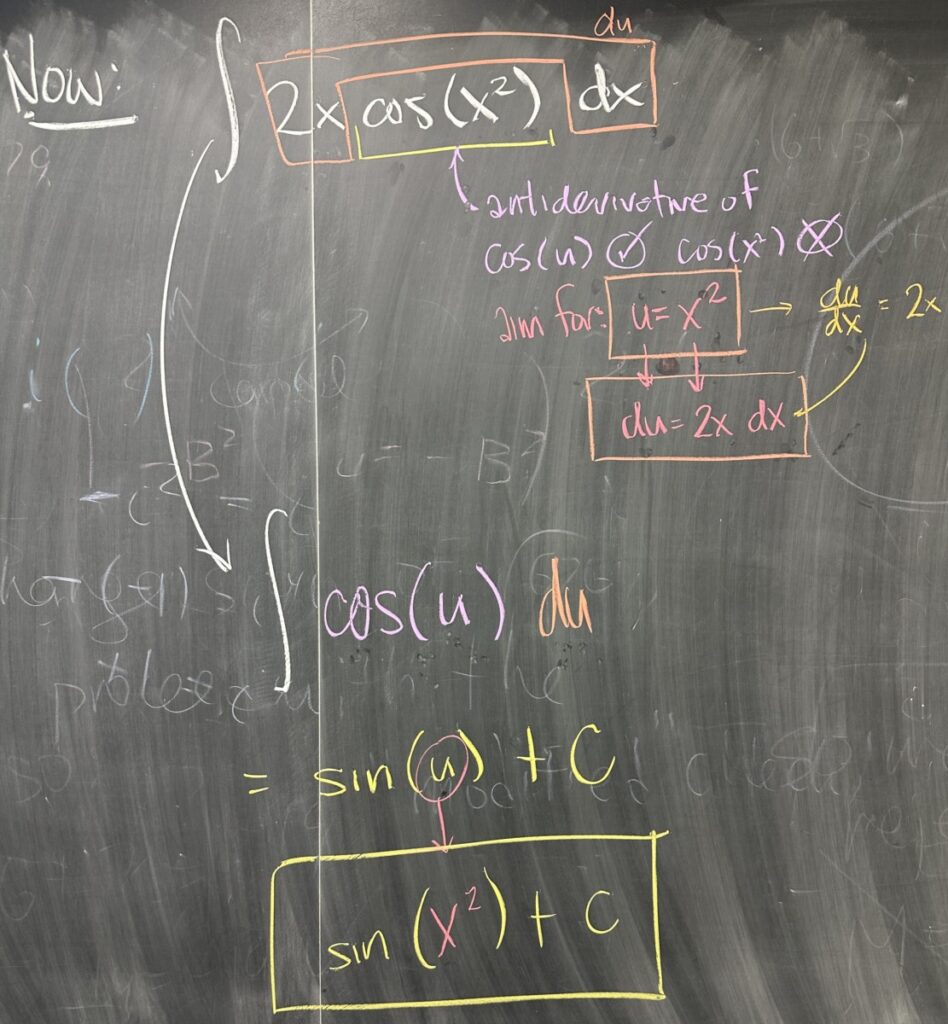
The point of reviewing the chain rule was to prepare for the technique we will use to “undo” it. “u-Substitution” is the antiderivative version of the chain rule for derivatives. In it, we take a similar approach as with the chain rule — we look for “inner functions” to substitute. In this case, we are taking the antiderivative of the derivative we just found (so we definitely know what the answer should be).
The process of substitution is similar to that of the chain rule, but the execution is different. In the chain rule, we multiplied by \(\frac{du}{dx}\) — and here in the antiderivative case, we will factor out the \(\frac{du}{dx}\).
Here, we choose \(u = x^2\) (so that we end up with \(\cos(u)\) instead of \(\cos(x^2)\)), which gives us \(\frac{du}{dx} = 2x\), or \(du = 2x\,dx\).
Back to our integral, we see that we already have \(2x\,dx\) as a factor, so we replace that with \(du\). Then we also replace \(x^2\) with \(u\) to get \(\int \cos(u)\, du\). This is a simple matter of finding the antiderivative for cosine, which is sine: \[\int\cos(u)\,du = \sin(u) + C = \sin(x^2) + C\]
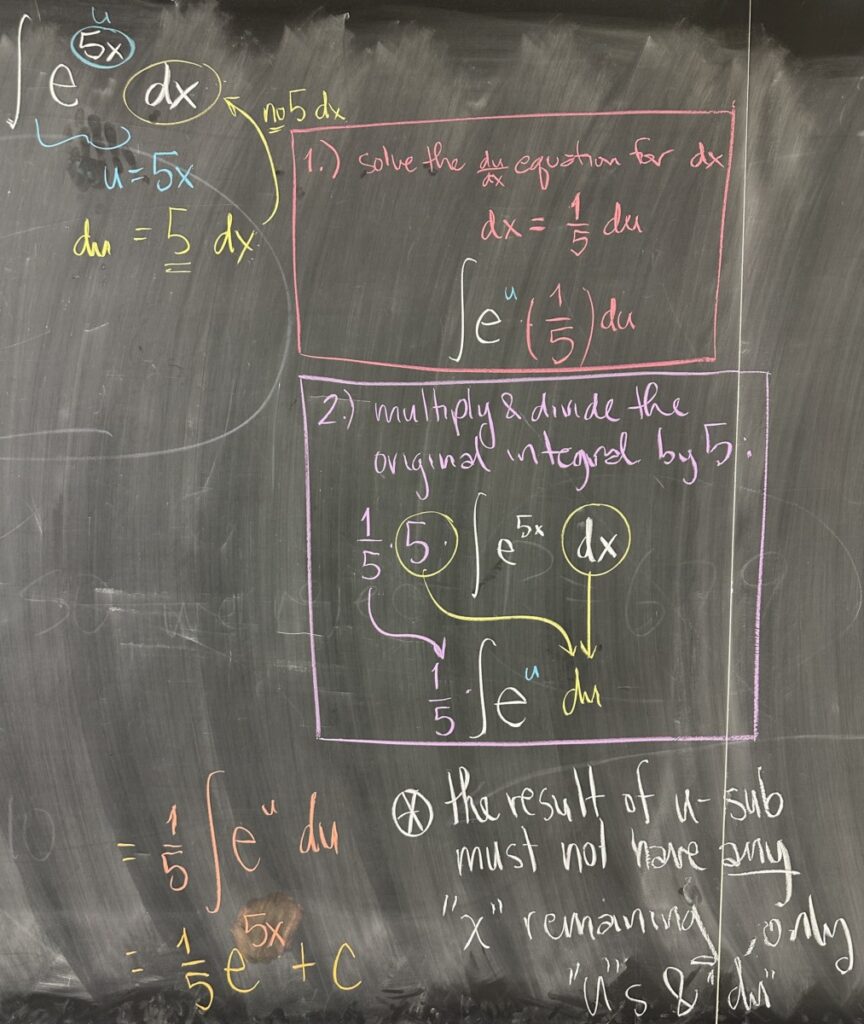
The tricky thing is, though, that we will not always have exactly \(du\) as a factor in our initial integral. In this example, we target the exponent of \(e\) as our substitution. If we choose \(u = 5x\), then \(du = 5\,dx\) — which is not a factor of our integral.
There are two ways of resolving this issue:
- Option 1: rewrite \(du = 5\,dx\) in terms of the factors we do have (we only have \(dx\)). So \(dx = \frac{1}{5}\,du\)
- Option 2: multiply and divide by any missing factors (we have \(dx\), so the only missing factor is \(5\)). So \(\int e^{5x}\,dx = \frac{1}{5}\int 5 e^{5x}\,dx\)
In option one, we manipulate the \(du\) equation; and in option two, we instead manipulate the original expression of the integral. Use whichever method makes the most sense to you — in either option, we end up with the same result after substitution: \[\int e^{5x}\,dx = \frac{1}{5}\int e^u\, du\]
It is essential that the result after substitution has no remaining instances of the original variable — in this case, no \(x\) and no \(dx\).
Now that the substitution is complete, it is an easy antiderivative: \[\frac{1}{5}\int e^u\,du =\frac{1}{5} e^u + C = \frac{1}{5}e^{5x} + C\]
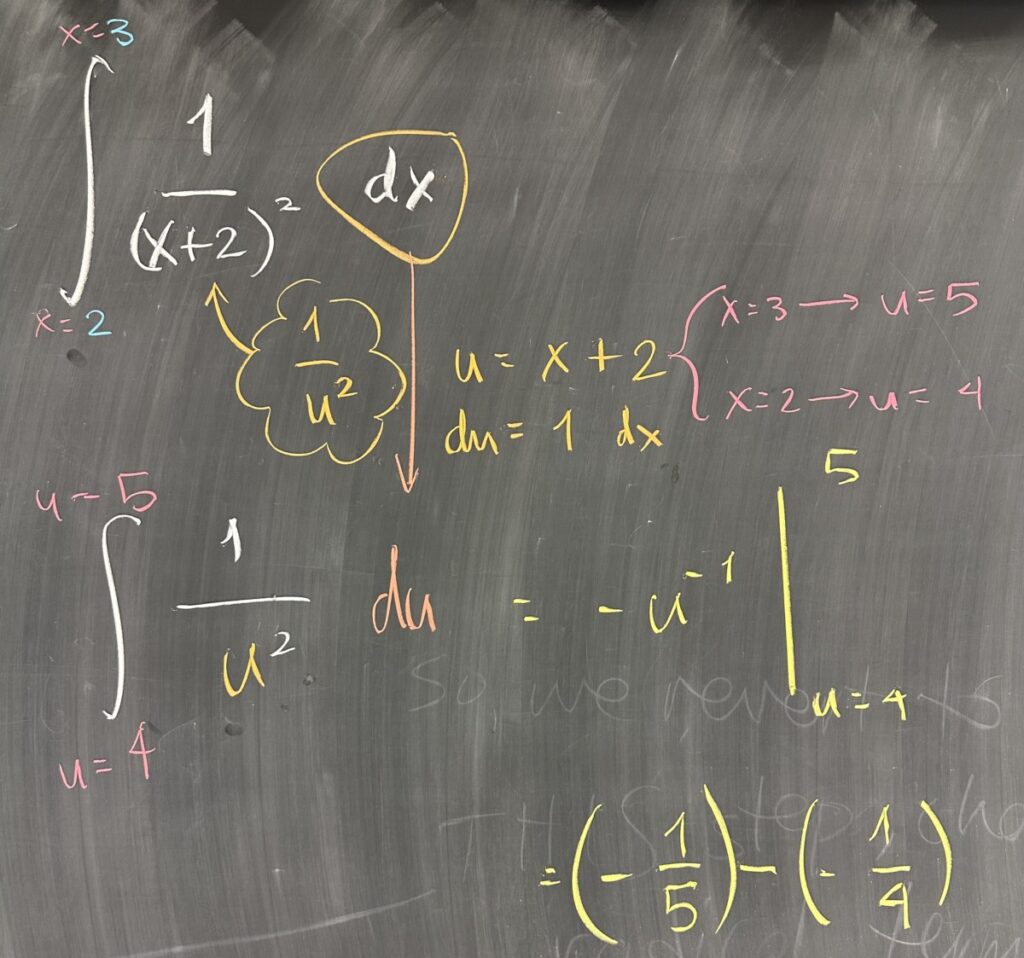
In the final example, we consider u-Substitution in the context of a definite integral. A neat trick is available to us here, specifically because (as a definite integral problem) our answer will be a number rather than a function.
From the initial integral, we identify a promising substitution: \(u = x+2\). It stands out because this substitution would have us integrate \(\frac{1}{u^2}\), a.k.a. \(u^{-2}\). That would be a straightforward antiderivative to find.
In order to see if our desired u-Substitution will work, we must be able to factor out \(du\) from our original integral. The choice of \(u = x+2\) would give us \(du = 1\,dx\). Essentially this means that we may swap \(dx\) for \(du\) without any additional factors. So the u-Substitution in the indefinite integral context would be: \[\int \frac{1}{(x+2)^2}\,dx = \int u^{-2}\,du\]
This is excellent because the chosen u-Substitution does not leave any \(x\) or \(dx\) in the result.
The neat trick that we can use is to convert our initial \(x\)-bounds into \(u\)-bounds. Since \(u = x+2\), we can tell that \(x=2\) would correspond to \(u = 2 + 2\), and we can also tell that \(x=3\) would correspond to \(u = 3 + 2\). So the u-Substitution in the definite integral context would be: \[\int_2^3 \frac{1}{(x+2)^2}\,dx = \int_4^5 u^{-2}\,du\]



Recent Comments