Hi everyone! Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Lesson 7: The inverse of a function
Topic. This lesson covers Session 7: The inverse of a function
Learning Outcomes.
- Identify one-to-one functions and understand the connection to inverse functions.
- Form connections between the definition of inverse functions, the notation of inverse functions, and the application of inverse functions.
- Find the inverse of a function graphically and algebraically.
WeBWorK. There is one WeBWorK assignment on today’s material:
- Functions – Inverse Functions
Additional Video Resources.
Question of the Day: What is the opposite of $x^3$?
Topic 1
Definition. A function $f$ is called one-to-one (or injective), if two different inputs $x_{1} \neq x_{2}$ always have different outputs $f\left(x_{1}\right) \neq f\left(x_{2}\right)$.
Example. Consider the functions $f(x)=x^2$ and $g(x)=x^3$, shown in the diagram below. Are either of these functions one-to-one?
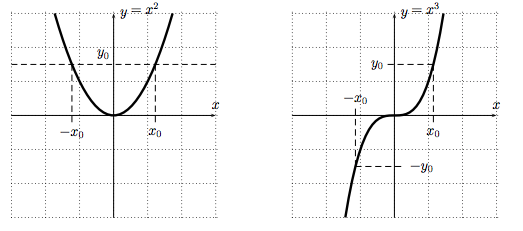
Observation (Horizontal Line Test). A function is one-to-one exactly when every horizontal line intersects the graph of the function at most once.
A function is one-to-one when each output is determined by exactly one input. Therefore we can construct a new function, called the inverse function, where we reverse the roles of inputs and outputs.
Definition 7.5. Let $f$ be a function with domain $D_{f}$ and range $R_{f},$ and assume that $f$ is one-to-one. The inverse of $f$ is a function $f^{-1}$ so that
$$f(x)=y \text{ means precisely that } f^{-1}(y)=x$$

Example. Find the inverse of each function:
- $f(x)=2x-7$
- $g(x)=\sqrt{x+2}$
- $h(x)=\frac{x+1}{x+2}$
VIDEO: Finding the Inverse of a Function
Video by Irania Vazquez
Exit Question
Find the inverse of $f(x)=x^3 + 7$
Answer
$f^{-1}(x)=\sqrt[3]{x-7}$
Good job! You are now ready to practice on your own – give the WeBWorK assignment a try. If you get stuck, try using the “Ask for Help” button to ask a question on the Q&A site.


