Table of Contents
Hi everyone! Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Lesson 5: Basic functions and transformations
Topic. This lesson covers Session 5: Basic functions and transformations
Learning Outcomes.
- Translate between geometric transformations (shifting, stretching, flipping) in either direction (vertically, horizontally) and the corresponding algebraic transformations of a function
- Identify even and odd symmetries.
WeBWorK. There are two WeBWorK assignments on today’s material:
- Functions – Translations
- Functions – Symmetries
Additional Video Resources.
Question of the Day: When you flip a graph over, what happens to the formula?
Transformations of graphs
Shifting a graph up or down: Add or subtract a number $c$ to the output $f(x)$, so $y=f(x)+ c$.
- Consider the graph of a function $y=f(x)$. Then the graph of $y=f(x)+c$ is that of $y=f(x)$ shifted up or down by $c$. If $c$ is positive, the graph is shifted up, if $c$ is negative, the graph is shifted down.
Shifting a graph left or right: Add or subtract a number $c$ to the input $x$, so $y=f(x+c)$
- Consider the graph of a function $y=f(x)$. Then the graph of $y=f(x+c)$ is that of $y=f(x)$ shifted left or right by $c$. Careful: If $c$ is positive, the graph is shifted left, if $c$ is negative, the graph is shifted right.
Stretching or compressing a graph vertically: Multiply the output $f(x)$ by a positive number $c$, so $y=c\cdot f(x)$
- Consider the graph of a function $y=f(x)$ and let $c>0$. Then the graph of $y=c\cdot f(x)$ is that of $y=f(x)$ stretched away or compressed towards the $x$-axis by a factor $c$. If $c>1$, the graph is stretched away from the $x$-axis, if $0<c<1$ then the graph is compressed towards the $x$-axis.
Stretching or compressing a graph horizontally: Multiply the input $x$ by a positive number $c$, so $y=f(c\cdot x)$
- Consider the graph of a function $y=f(x)$ and let $c>0$. Then the graph of $y=f(c\cdot x)$ is that of $y=f(x)$ stretched away or compressed towards the $y$-axis by a factor $c$. If $c>1$, the graph is stretched away from the $y$-axis, if $0<c<1$ then the graph is compressed towards the $y$-axis.
Reflect a graph horizontally or vertically:
- To reflect vertically (across the $x$-axis), multiply the output of the function by $-1$, so $y=- f(x)$.
- To reflect horizontally (across the $y$-axis), multiply the input of the function by $-1$, so $y=f(-x)$.
VIDEO: Transformations of functions
Video by Irania Vazquez
Symmetries: Odd and Even functions
Definition. A function $f$ is called even if $f(-x)=f(x)$ for all $x$.
Similarly, a function $f$ is called odd if $f(-x)=-f(x)$ for all $x$
Observation.
- An even function is symmetric with respect to the $y$-axis (if you reflect the graph horizontally across the $y$-axis, you end up with the same graph – the left side is a mirror image of the right side).
- An odd function is symmetric with respect to the origin (if you rotate the graph $180^\circ$ about the origin, you end up with the same graph).
VIDEO: Odd and Even Functions
Video by Irania Vazquez
Exit Question
Is the function shown below odd or even?
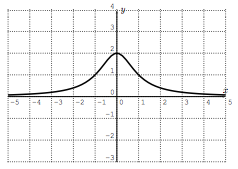
Answer
The function is even, since the right side looks like a mirror image of the left side.
Good job! You are now ready to practice on your own – give the WeBWorK assignment a try. If you get stuck, try using the “Ask for Help” button to ask a question on the Q&A site.


