Lesson 1: The Absolute Value

Hi everyone! Read through the material below, watch the videos, and follow up with your instructor if you have questions.

Question of the Day: If $|x|=5$ then what does $x$ equal?

Background Regarding Numbers

Absolute Value

Definition. The absolute value of a real number $c$, denoted by $|c|$, is the non-negative number which is equal in magnitude (or size) to $c$, i.e., is the number resulting from disregarding the sign:

$|c|=\left\{ \begin{array}{cl}
c, & \text { if } c \text { is positive or zero } \\
-c, & \text { if } c \text { is negative }
\end{array}$

Example 1.

1. $|-4|=$,
2. $|4|=$
3. For which real numbers $x$ do you have $|x|=3$?
4. Solve for $x:|3 x-4|=5$
5. Solve for $x:\quad -2 \cdot|12+3 x|=-18$

Inequalities and Interval Notation

In this section we need to discuss two ideas:

First, the notion of ordering or inequality. For example:

$4<9$ reads as 4 is less than 9
$-3 \leq 2$ reads as -3 is less than or equal to 2
$\frac{7}{6}>1$ reads as $\frac{7}{6}$ is greater than 1
$2 \geq-3$ reads as 2 is greater than or equal to -3

The second is the called intervals – an interval is a set of numbers on the number line lying (for example) between two endpoints. We can give an interval in three ways: using inequalities, using interval notation, or by drawing a number line. It’s important to be able to describe the same interval in different ways. The following table shows how these three methods are connected:

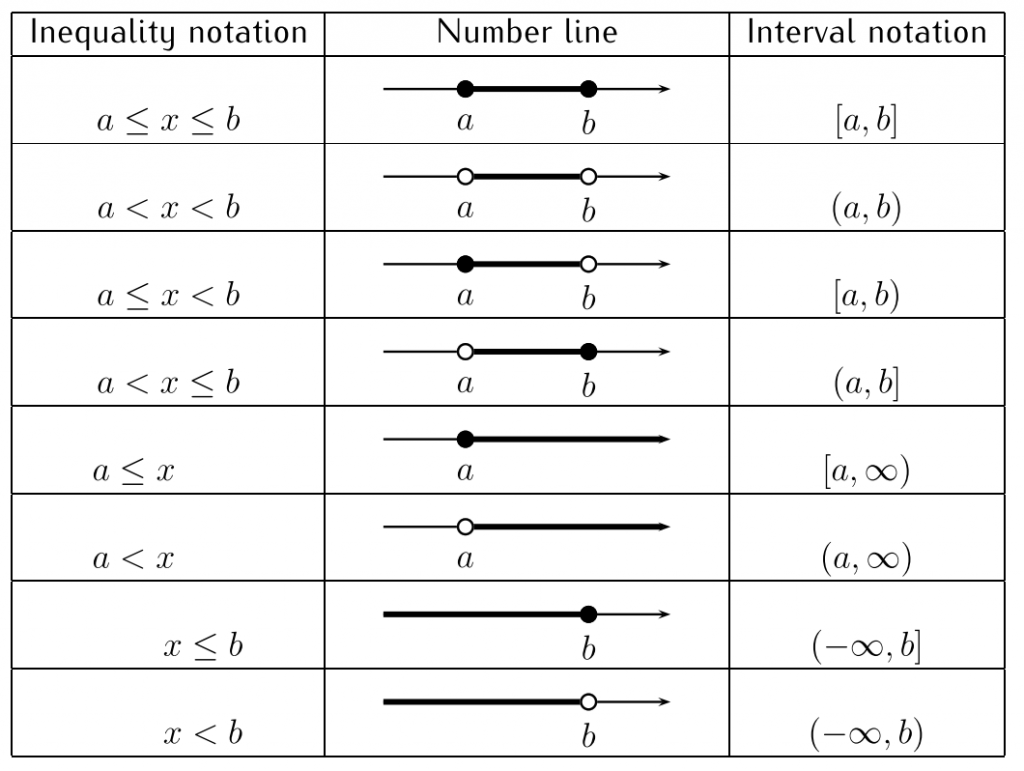
Absolute Value Inequalities

Example 2. Solve for $x$ :

• $|3 x-5| \geq 11$
• $|12-5 x| \leq 1$
• $|x+7|\leq -3$, $|x+7|\geq -3$

Good job! You are now ready to practice on your own – give the WeBWorK assignment a try. If you get stuck, try using the “Ask for Help” button to ask a question on the Q&A site.