Lab 5
1.Description
This is a program to approximate the square root of a number using Babylonian algorithm. Babylonian algorithm works by averaging an overestimate of the square root with an underestimate to provide a better estimate of the square root. This process when repeated infinitely will converge to the actual square root but since we neither have infinite time nor resources, we must settle for computing the square root to within a certain tolerance for practical purposes.
2.Code
#include
#include
#include
using namespace std;
double Babylonian(double);
int main(void){
double num,babylonian;
cout << "Enter a number to approximate it's square root: "; cin >> num;
babylonian = Babylonian(num);
cout << "Using sqrt() the result is: " << sqrt(num) << endl;
cout << "Difference between sqrt() and babylonian is: " << sqrt(num) - babylonian << endl;
return 0;
}
double Babylonian(double num){
const double TOLERANCE = 0.00001;
double diff;
int n = 0;
vector x;
x.reserve(20);
x.push_back(num/2); //x_0 = x/2 as our first guess.
do{
cout << "Itteration #" << n+1 << endl;
x.push_back( (x[n] + num/x[n])/2 ); //x_n+1 = formula for next n.
cout << "Babylonian Square Root Aprox is " << x[n+1] << endl;
diff = abs(x[n+1] - x[n]);
cout << "Difference of x_n+1 - x_n: " << diff << endl << endl; n++; }while( diff >= TOLERANCE );
return x[n];
}
3.Screenshots
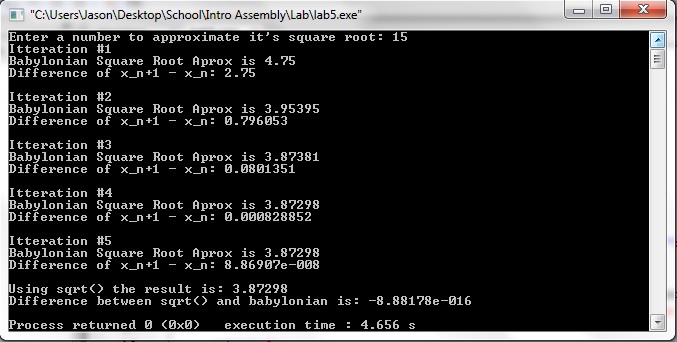
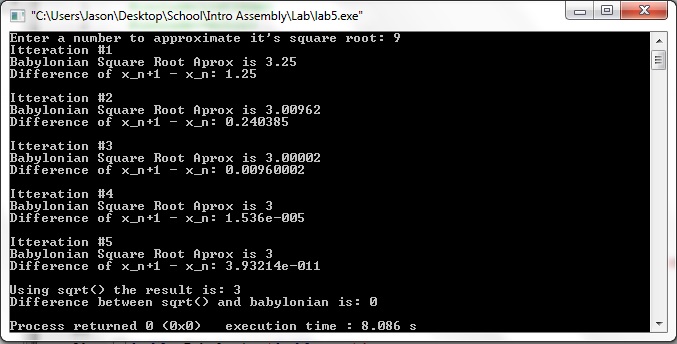



Leave a Reply