Program Description:
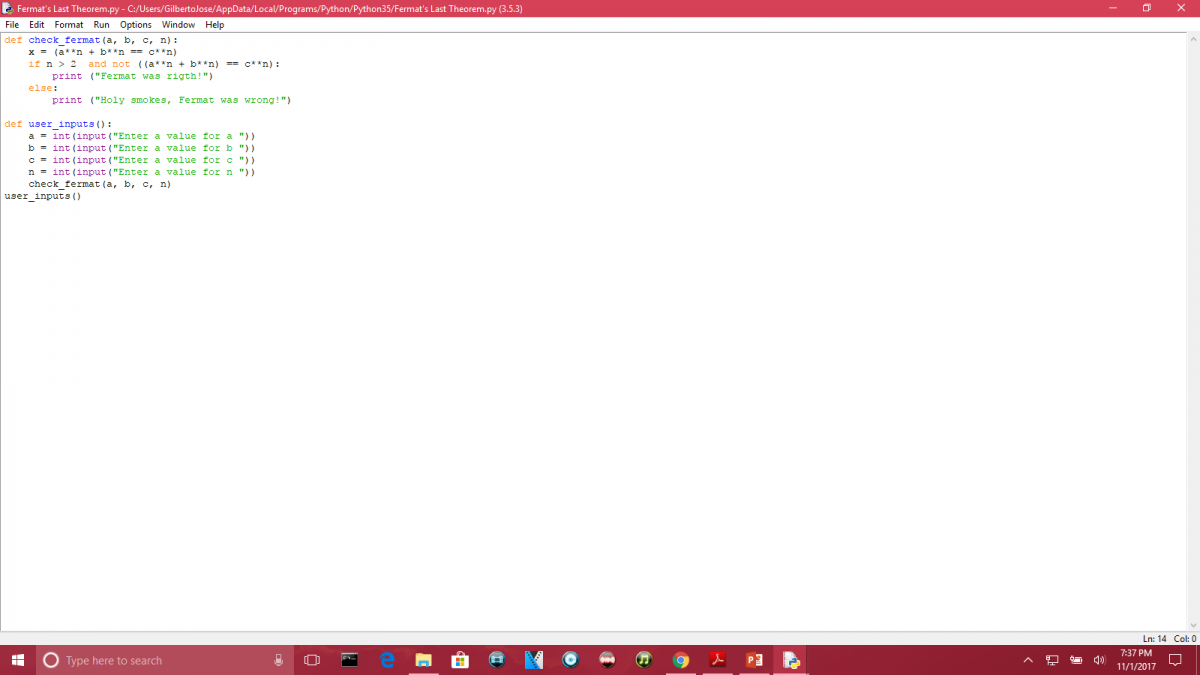
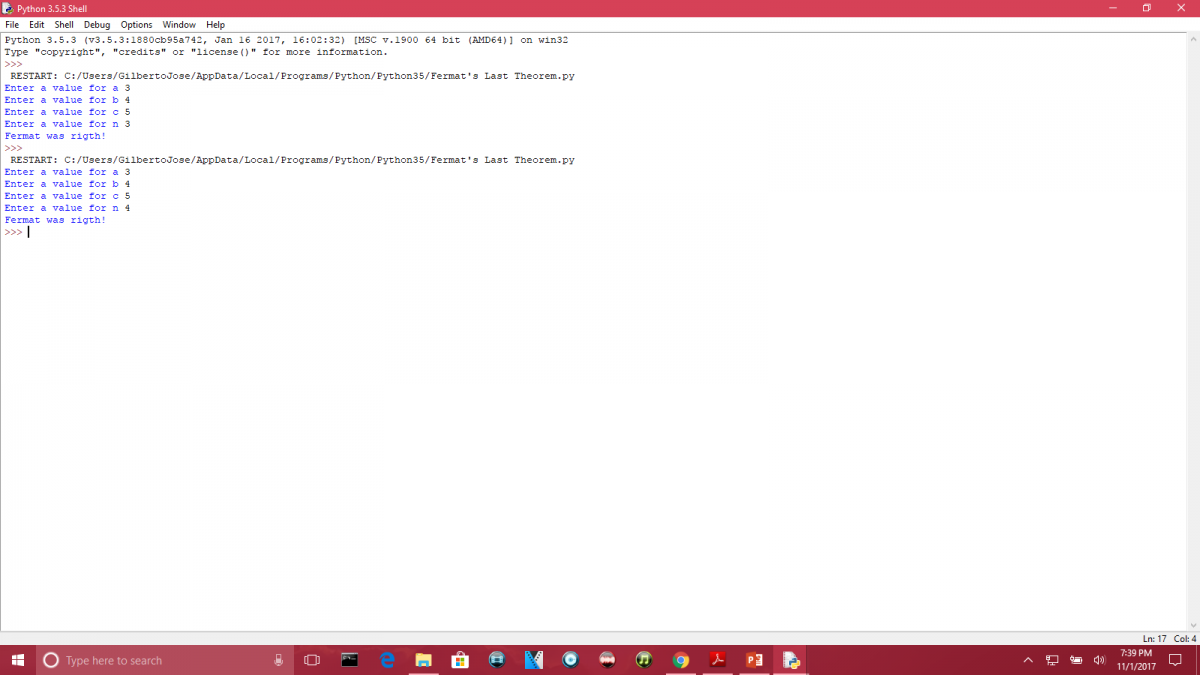
The purpose of this lab was to create a program where we test Fermat’s theory. Fermat’s theory says that positive integer give to three constant to the give equation, a^n + b^n = c^n, that makes the equation satisfy with “n” = 2, it would not satisfy the equation having the value for “n” to be greater than 2. For example, if a = 3, b = 4, c = 5 and n = 2 the results will be “9 + 16 = 25” which actually satisfy the equation. However, when we increase the value of n, the equation would not be satisfy. Below is going to be the program itself so you can try it your self and the console showing the results were it proves Fermat’s theorem with the values of a, b, and c as presented in the example.
Program:
def check_fermat(a, b, c, n):
x = (a**n + b**n == c**n)
if n > 2 and not ((a**n + b**n) == c**n):
print (“Fermat was rigth!”)
else:
print (“Holy smokes, Fermat was wrong!”)
def user_inputs():
a = int(input(“Enter a value for a “))
b = int(input(“Enter a value for b “))
c = int(input(“Enter a value for c “))
n = int(input(“Enter a value for n “))
check_fermat(a, b, c, n)
user_inputs()
How does it supposed to look on python:
Console (User inputs):