Here are a couple of the examples we went through in class, regarding how to solve simple trigonometric equations.  We find the solution sets using both the graph of the function and the unit circle:

Example 1: Solve sin x = 0:

The solutions of this equation correspond to the x-intercepts of the graph of y = sin x.

(Make sure you understand why: the graph of a function y = f(x) intersects the x-axis exactly when f(x)=0!)

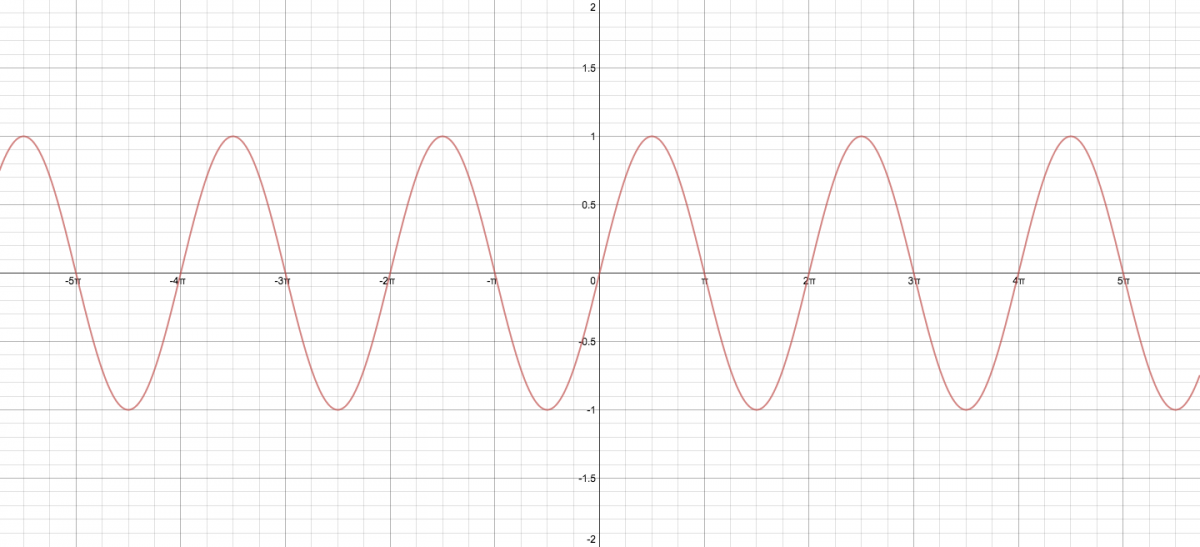
Here is the graph of y = sin x:

We see that the x-intercepts of y = sin x occur at  (for any integer n).  Hence that is the solution set of the equation

(Click on the graph to enlarge it–or better, make your own graph in Desmos!)

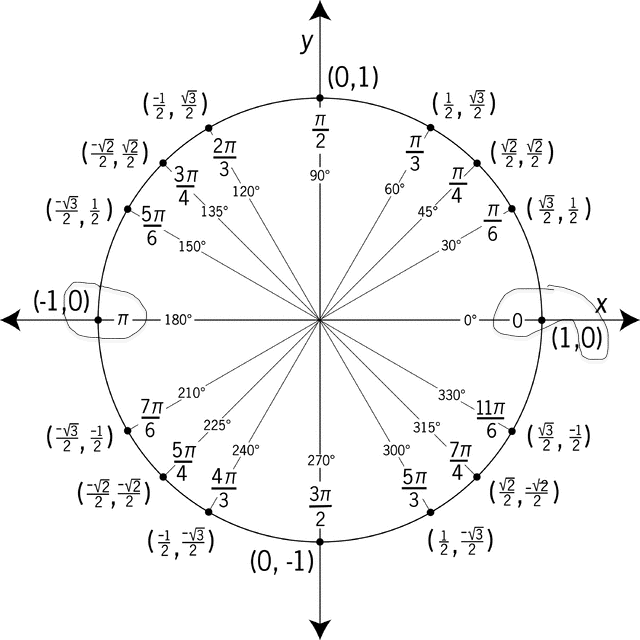
We can also get this solution set from the unit circle. To find the solutions of sin x = 0, we want o find the angles on the unit circle such that the y-coordinate of the point equals 0. Looking at the unit circle below, we see this occurs at the angles 0 and  (circled):

But we also hit those same points, and hence the same values of the sine function, when we go around the circle a full revolution in either direction, i.e., if we add or subtract any integer multiple of to these two basic solutions.

Hence, the complete solution set consists of
and

Combining these, we see that get the same solution set as above:

(where n = 0, 1, 2, 3, …)

Example 2: Solve cos x = -1/2:

To find the solutions of cos x = -1/2, we need to find the angles on the unit circle such that the x-coordinate of the point is -1/2. This occurs at the angles and  (find these points on the unit circle!).

But once again, we also have a solution when we go around the circle a full revolution in either direction, i.e., if we add or subtract any integer multiple of to these two basic solutions. Hence, the solutions of cos x = -1/2 are

and  (where n = 0, 1, 2, 3, …)

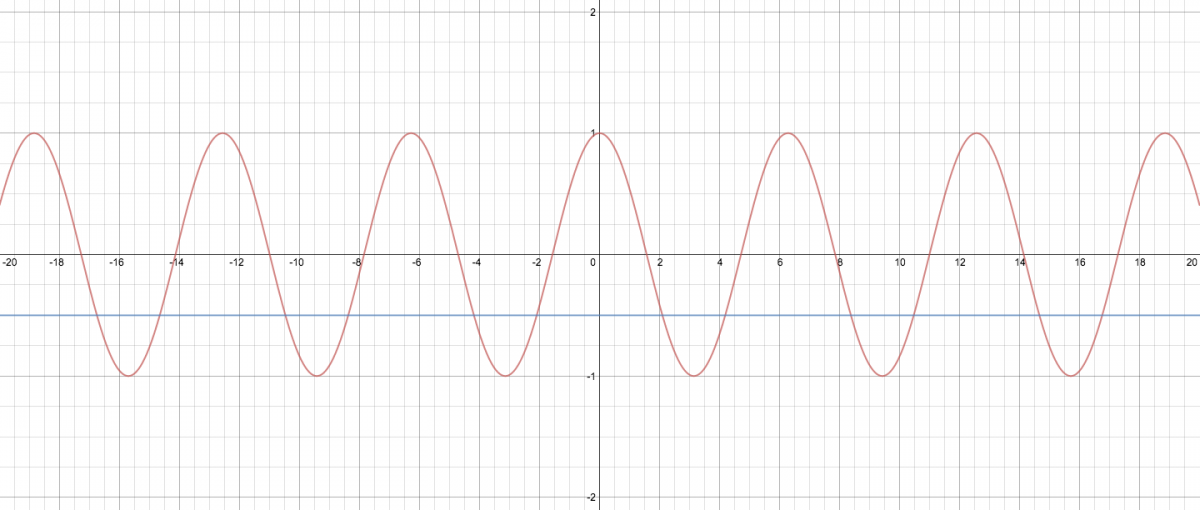
We can find this solution set by looking at where the graph of y = cos x intersects with the line y = -1/2 (set up this graph in Desmos and look at the points of intersection–they will correspond exactly to the solution set given above):