Loading...
You are viewing WeBWorK Q&A Example Site. Here, you can ask questions and discuss WeBWorK homework problems, and also see what other students have been asking.
Recent Activity
 A Question from City Tech StudentShow WeBWorK Problem
A Question from City Tech StudentShow WeBWorK Problem
Differentiate f(x)=x2−3x+2x2.
Answer: dfdx= ___My question:I don't understand why my answer isn't right- Question from a StudentShow WeBWorK Problem
f(x)={x2+4x−21−x2+9,x≠3C,x=3
What value of C would make f(x) continuous at x=3? ___- Decimal approximations are not allowed for this problem.
- Compute the exact value for C and express your answer algebraically.
My question:How do I do it? - Decimal approximations are not allowed for this problem.
- Question from a StudentShow WeBWorK Problem
Continuous Functions
A function f(x) is continuous at x=a if:- a is in the domain of f(x), i.e. f(a) exists
- limx→af(x) exists, i.e. both one-sided limits exist and are equal
- limx→af(x)=f(a)
Reasons why f(x) might fail to be continuous: f(a) does not exist limx→af(x) doesn't exist or both exist, but don't match 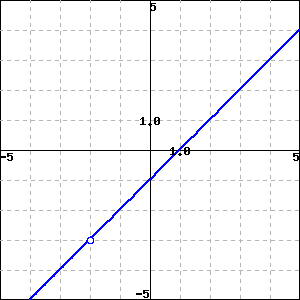
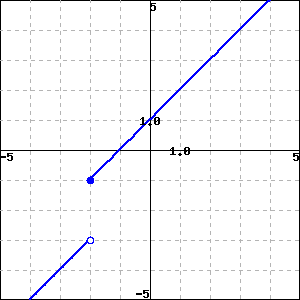
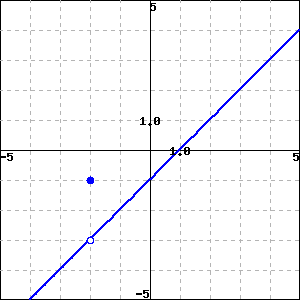
f(x)=(x−1)(x+2x+2) f(x)={<br/><br/>x−1,x<−2x+1,x≥−2 f(x)={(x−1)(x+2x+2),x≠−2−1,x=−2 Practice
Determine the most accurate statement for each of the following graphs: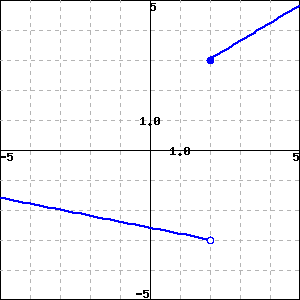
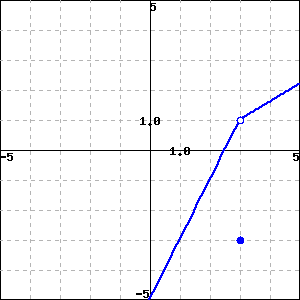
___ A. f(x) is continuous at x=2.
___ B. f(x) is not continuous at x=2 because f(2) is undefined.
___ C. f(x) is not continuous at x=2 because limx→2f(x) does not exist.
___ D. f(x) is not continuous at x=2 because f(2) and limx→2f(x) exist, but are not equal.
___ A. f(x) is continuous at x=3.
___ B. f(x) is not continuous at x=3 because f(3) is undefined.
___ C. f(x) is not continuous at x=3 because limx→3f(x) does not exist.
___ D. f(x) is not continuous at x=3 because f(3) and limx→3f(x) exist, but are not equal.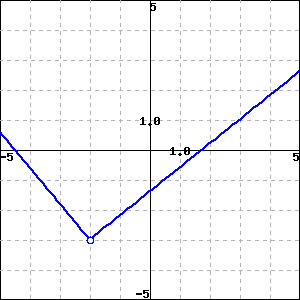
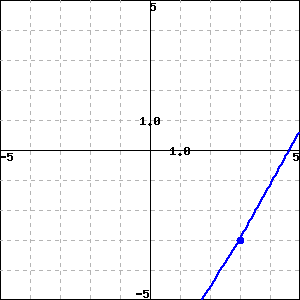
___ A. f(x) is continuous at x=−2.
___ B. f(x) is not continuous at x=−2 because f(−2) is undefined.
___ C. f(x) is not continuous at x=−2 because limx→−2f(x) does not exist.
___ D. f(x) is not continuous at x=−2 because f(−2) and limx→−2f(x) exist, but are not equal.
___ A. f(x) is continuous at x=3.
___ B. f(x) is not continuous at x=3 because f(3) is undefined.
___ C. f(x) is not continuous at x=3 because limx→3f(x) does not exist.
___ D. f(x) is not continuous at x=3 because f(3) and limx→3f(x) exist, but are not equal.
Note: In order to get credit for this problem all answers must be correct.My question:I'm not sure how to answer this question. Is it possible that there is more than one correct statement for an image? - a is in the domain of f(x), i.e. f(a) exists
Explore Questions
Use the filters below to navigate the questions that have been posted. You can select questions by course, section, or a specific WeBWorK problem set.
- Select Course
- Select Section/Faculty
- Select Problem Set



