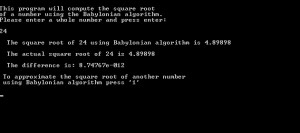
Description:

This Lab focused on a different method of acquiring the square root of a number, the “Babylonian” way. This method emphasizes a trial and error style of process. The algorithm and method appears fairly simple utilizing a program, yet one could see
that if performed by hand the calculations could become tedious and redundant. Interestingly enough the tolerance for this lab was specified at .00001 which leaves almost no room for error, adding another 0 gets us to a point where the
Babylonian method is almost error free when compared to a common sqrt() function or a calculator.

Code:

// Yevgeniy Babkin lab # 5 Babylonian Algorithm

#include 
using namespace std;
int main()

{
	system("CLS");

cout<<endl;
// increasing the tolerance by one more zero makes this code almost equivalent to the sqrt() function
double t = .00001;
double x = 0;
double guess = 0;
double current = 0;
double diff=1;
double b=0;
int s=0;
cout << "This program will compute the square root\n";
cout << "of a number using the Babylonian algorithm.\n";
cout << "Please enter a whole number and press enter:\n\n"; cin >> x;

guess = x/2;

while(t <= diff)
{
    current = (guess + (x/guess) )/2;
    diff = abs(current - guess);
    guess = current;

    b = sqrt(x);

}

cout << " \n  The square root of "<< x << " using Babylonian algorithm is " << current<<endl<<endl;
cout << "  The actual square root of "  <<  x  <<  " is "  << b << endl;
cout << "\n  The difference is: " << abs(current - b)<<endl;

cout << "\n To approximate the square root of another number \n using Babylonian algorithm press '1' " <<endl<<endl; cin>> s;
//repeat statement
    if(s != 1 )
	    return 0;
    else
	    return main();
}

Screenshot: