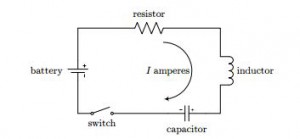
Electric circuits can consist of a wide variety of complex components. These may be set up in series, or in parallel, or even as combinations of both. However, we’ll be considering only series circuits with especially simple components: resistors, inductors, and capacitors, along with some form of voltage supply.

To start with, let’s consider the picture of a simple series circuit in which one of each of the components that we mentioned above appears:

 

• L is a constant representing inductance, and is measured in Henry
• R is a constant representing resistance, and is measured in ohms
• C is a constant representing capacitance, and is measured in farads
• E represents the electromotive force, and is measured in volts. It is not necessarily a constant, and may be a function of time

Let Q(t) be the charge in the capacitor at time t (Coulombs). Then dT /dt is called the current, denoted I. The battery produces a voltage (potential difference) resulting in current I when the switch is closed. The resistance R results in a voltage drop of RI. The coil of wire (inductor) produces a magnetic field resisting change in the current. The voltage drop created is L(dI/dt). The capacitor produces a voltage drop of Q/C. Unless R is too large, the capacitor will create sine and cosine solutions and, thus, an alternating flow of current. Kirchhoff Law states that “The sum of the voltage drops across each component in a circuit is equal to the voltage, E, impressed upon the circuit.” so

Restating Kirchhoff’s second law in abbreviated form, we get the following:

sum of the voltage drops = E,

which may be restated as:

inductor voltage drop + resistor voltage drop + capacitor voltage drop = E,

into which we may substitute the actual voltage drops that we mentioned above, to get:

(1)	LI′ + RI + q/C = E.

But, also according to physics, I = q′, so substituting, we can rewrite the equation purely in terms of the charge, q, rather than a mixture of charge and current:

(2)	Lq″ + Rq′ + q/C = E,

or alternatively, if we differentiate equation (1) and use the same substitution, we get an equation purely in terms of current:

(3)	L I″ + R I′ + I/C = E′.

We will be mainly concerned with using the last of these three equivalent forms.

Notice that equation (3) is linear with constant coefficients, so in this case when
E′ = 0, (the homogeneous case), it may be solved very easily, even by hand.

The form of E′ will determine the method necessary when solving the non-homogeneous case by hand. We would need to use either undetermined coefficients, or variation of parameters.

An Example:

E(t) = 2e^t, R= 5Ω, C= 1/6 F, L= 1H

 

E(t)= Q`R + Q/R + Q/C + LQ“

=> 2e^t = Q`*5 + Q/(1/6) + L*Q“

=>2e^t = Q“ +5Q` + 6Q

 

r2 + 5r + 6 = 0

r2 + 3r + 2r + 6 =0

(r+3)(r+2) = 0

r = -3

r = -2

Q = Ae-3t + Be-2t

Guess:

Q = Ce^t

Q` = Ce^t

Q“ = Ce^t

 

Ce^t  + 5Ce^t + 6 Ce^t = 2 e^t

12Ce^t  = 2e^t

6Ce^t = e^t

C = 1/6

Q = Ae^(-3t) + Be^(-2t) + (1/6)e^t

Initial charge Q(0) = 11C

Initial Current I(0) = -18A

 

Take Q` and plug in

Q = Ae^(-3t) + Be^(-2t) + (1/6)e^t

Here are some videos which may also help to solve electrical Circuit in Differential Equation