Hi everyone! Read through the material below, watch the videos, and send me your questions. Don’t forget to complete the Daily Quiz (below this post) before midnight to be marked present for the day.
Lesson 18: Addition of angles and multiple angle formulas
Lesson Date: Thursday, April 16th.
Topic: This lesson covers Chapter 18: Addition of angles and multiple angle formulas.
WeBWorK: There are two WeBWorK assignments on today’s material, due next Thursday 4/23:
Trigonometry – Sum and Difference Formulas
Trigonometry – Double and Half Angle Formulas
Lesson NOtes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Question of the Day: Suppose we know the values of the trig functions of two angles $a$ and $b$. Can we use them to find the values of the trig functions of the angle $a+b$?
Today, we will see how we can do exactly that – the idea is to work with formulas that allow us to calculate, for example, $\sin(a+b)$ and $\cos(a+b)$ based on the values of $\sin(a),\cos(a),\sin(b),$ and $\cos(b)$.
NOTE: We often use greek letters for angles — this helps us keep track of what’s an angle and what’s not. The most common are the greek letters alpha $\alpha$ and beta $\beta$. We’ll be using these instead of $a$ and $b$.
Warning: the videos for today’s lecture are *quite long* – however, they consist almost entirely of examples, with a lot of explanation. Feel free to skip around, or to try the WeBWorK first (if you get stuck, the videos might help).
Addition and Subtraction of Angles
Proposition 18.1. For any angles $\alpha$ and $\beta$,
- $\sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta$
- $\sin (\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta$
- $\cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta$
- $\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta$
- $\tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}$
- $\tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}$
Where did these formulas come from!?
Great question! To answer it, you need to see the *proof* of these formulas – this appears in your book in Chapter 18.
Now, we are going to see how these formulas let us calculate the values of trig functions at many different angles, based on just a few common angles (such as those listed in the table below – if you don’t know them, this is a great time to learn them!).
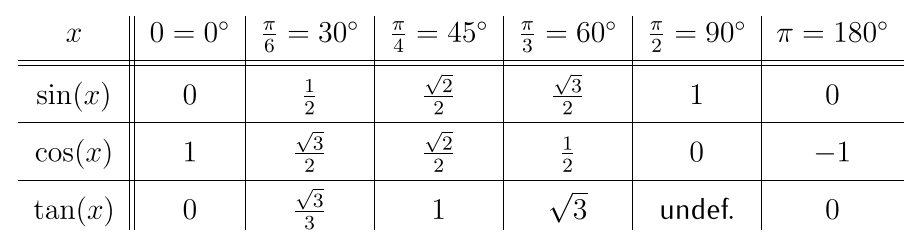
Example 18.2. Find the exact values of the trigonometric functions:
a) $\cos \left(\frac{\pi}{12}\right)$
b) $\tan \left(\frac{5 \pi}{12}\right)$
c) $\cos \left(\frac{11 \pi}{12}\right)$
VIDEO: Example 18.2 applying angle sum and difference formulas
Double and Half Angles
Proposition 18.5. Let $\alpha$ be any angle. Then we have the half-angle formulas:
$\sin \frac{\alpha}{2} =\pm \sqrt{\frac{1-\cos \alpha}{2}}$
$\cos \frac{\alpha}{2} =\pm \sqrt{\frac{1+\cos \alpha}{2}}$
$\tan \frac{\alpha}{2} =\frac{1-\cos \alpha}{\sin \alpha}=\frac{\sin \alpha}{1+\cos \alpha}=\pm \sqrt{\frac{1-\cos \alpha}{1+\cos \alpha}}$
and the double-angle formulas:
$\sin (2 \alpha) =2 \sin \alpha \cos \alpha$
$\cos (2 \alpha) =\cos ^{2} \alpha-\sin ^{2} \alpha=1-2 \sin ^{2} \alpha=2 \cos ^{2} \alpha-1$
$\tan (2 \alpha) &=\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}$
Example 18.6. Find the exact values of the trigonometric functions:
a) $\sin \left(\frac{\pi}{8}\right)$
b) $\cos \left(\frac{9 \pi}{8}\right)$
c) $\tan \left(\frac{\pi}{24}\right)$
VIDEO: Example 18.6 applying half-angle formulas
Example 18.7. Find the trigonometric functions of $2\alpha$ when $\alpha$ has the properties below.
a) $\sin (\alpha)=\frac{3}{5},$ and $\alpha$ is in quadrant 1
b) $\tan (\alpha)=\frac{12}{5},$ and $\alpha$ is in quadrant 2
VIDEO: Example 18.7 applying double-angle formulas
That’s it for now. Take a look at the WeBWorK, and send me your questions!
-Prof Reitz
