Category: OpenLab Assignment

OpenLab #3: Advice for the future

May 9, 2019 / Jonas Reitz / 53 Comments

(Due Tuesday, 5/21/19, at the start of class). Imagine that you are invited to speak on the first day of MAT 2680, to give advice to entering students. Write at least three sentences responding to one or two of the following, describing what you would tell them.

What do you wish that you had been told at the start of this class, to help you succeed?
Choose one topic in the course that is especially challenging. Identify it, and give advice to students trying to master that topic.
What is the most important prior knowledge (not taught in the class) that you need in order to succeed? Why is it important?

Extra Credit. Respond to someone else’s comment. Do you agree? disagree? Have anything to add?

OpenLab #2: Numerical methods PROJECT – Scoring Guide

April 28, 2019 / Jonas Reitz / 0 Comments

Hi everyone,

Your overall grade (out of 20 possible) for the numerical methods project has been posted under Dashboard/OpenLab Gradebook. The scoring guide that I used to assess your work is given below. If you’d like more details about your score, please send me an email or ask me after class.

Regards,
Prof. Reitz

NUMERICAL METHODS PROJECT

SCORING GUIDE

20 points total (Written Assignment + Implementation)

WRITTEN ASSIGNMENT – OpenLab (5 points total):

1 point – 300 words minimum
2 points – Describe project & how it works, Describe process of building it (what tech did you use/why? Unexpected challenges?)
1 point – Why do we need numerical methods? Why is this assignment included in the class?
1 point – include link or state you will send by email

IMPLEMENTATION (15 points total):

3 points: General setup

2 points – Correct differential equation: dy/dx = x^2/(y-1)
1 point – Correct initial condition y(-1)= -0.5

4 points: Euler’s Method

2 points – functioning solution, displays x,y,f(x,y) at each stage
1 point – correct x-target value
1 point – four digits of accuracy after decimal: y(2)=-1.87228… (will accept -1.8722 or -1.8723), optimum # of steps 11795

4 points: Improved Euler’s Method

2 points – functioning solution, displays x,y,k1,k2 at each stage
1 point – correct x-target value
1 point – four digits of accuracy after decimal: y(2)=-1.87228… (will accept -1.8722 or -1.8723), optimum # of steps 291

4 points: Runge-Kutta Method

2 points – functioning solution, displays x,y,k1,k2,k3,k4 at each stage
1 point – correct x-target value
1 point – four digits of accuracy after decimal: y(2)=-1.87228… (will accept -1.8722 or -1.8723), optimum # of steps 12

OpenLab #2: Numerical Methods PROJECT – Part 2

March 19, 2019 / Jonas Reitz / 39 Comments

This post contains additional information related to the Numerical Methods Project earlier in the week, due April 4th.

Submission guidelines. Your completed project will consist of three elements:

A working numerical methods calculator using your choice of technology (spreadsheet, programming, mathematical software), as described in the previous post.
HOW TO SUBMIT:
- If your project is a spreadsheet, either share it with me (if it is in Google Docs or a similar cloud-based platform), or email the file to me as an attachment.
- If your project is code, please submit it using an online coding site like ideone.com – once your code is working on the site, you can simply submit a link. If you are using a programming language not supported by ideone.com, you can email the source code to me.
- If your project uses mathematical software, either share it with me (if it is in MatLab Online or a similar cloud-based platform), or email the file to me as an attachment.
Solutions to the following example using each of the three methods studied in class (Euler’s Method, Improved Euler’s Method, and Runge-Kutta), generated by your numerical methods calculator. Submit using the same method as in part 1.

Project Example. Given the differential equation $dy/dx = \frac{x^2}{y-1}$ and initial condition $y(-1)=-0.5$ , approximate the value of $y(2)$ using Euler’s Method, Improved Euler’s Method, and Runge-Kutta.

For each method, choose a step size that gives four correct digits following the decimal point. How many steps are required to obtain this level of precision?

NOTE: The actual solution is $y(2)=-1.87228$ …

Writing assignment. Write one or two paragraphs (minimum 300 words) responding to the following. Leave your response as a comment on this post.
1. Describe your project and how it works.
2. Describe the process of building your numerical methods calculator. What kind of technology did you decide to use, and why? Did you encounter any unexpected challenges in completing this project?
3. Why do we need numerical methods in addition to the other methods studied in the class?
4. Why is this assignment included in the class (instead of just computing the various methods using a calculator)?
5. Please include a link to your project (if it is online), or clearly state that you will be sending me the files by email (and don’t forget to do it!).

OpenLab #2: Numerical methods PROJECT – Example Data

March 14, 2019 / Jonas Reitz / 0 Comments

Below you will find complete solutions for the Example given the previous post – you can use this to test your project.

Example. Given the differential equation and initial condition , approximate the value of using step size

ACTUAL ANSWER: y(2.5) = 3.49201…

Euler’s Method
i	h	x_i	y_i	k = f(x_i,y_i)	y_(i+1)
0	0.05	1.5	2.2	0.6	2.23
1	0.05	1.55	2.23	0.67425	2.2637125
2	0.05	1.6	2.2637125	0.74903	2.301164
3	0.05	1.65	2.301164	0.8240397	2.342365985
4	0.05	1.7	2.342365985	0.8989889128	2.387315431
5	0.05	1.75	2.387315431	0.9735989982	2.435995381
6	0.05	1.8	2.435995381	1.047604158	2.488375588
7	0.05	1.85	2.488375588	1.120752581	2.544413217
8	0.05	1.9	2.544413217	1.192807443	2.60405359
9	0.05	1.95	2.60405359	1.26354775	2.667230977
10	0.05	2	2.667230977	1.332769023	2.733869428
11	0.05	2.05	2.733869428	1.400283836	2.80388362
12	0.05	2.1	2.80388362	1.465922199	2.87717973
13	0.05	2.15	2.87717973	1.52953179	2.95365632
14	0.05	2.2	2.95365632	1.590978049	3.033205222
15	0.05	2.25	3.033205222	1.650144125	3.115712428
16	0.05	2.3	3.115712428	1.706930708	3.201058964
17	0.05	2.35	3.201058964	1.761255718	3.289121749
18	0.05	2.4	3.289121749	1.813053901	3.379774445
19	0.05	2.45	3.379774445	1.862276305	3.47288826
20	0.05	2.5	y(2.5) = 3.47288826

Improved Euler’s Method
i	h	x_i	y_i	k1	z_(i+1)	k2	y_(i+1)
0	0.05	1.5	2.2	0.6	2.23	0.67425	2.23185625
1	0.05	1.55	2.23185625	0.6728114063	2.26549682	0.7476025438	2.267366599
2	0.05	1.6	2.267366599	0.746106721	2.304671935	0.8211456538	2.306547908
3	0.05	1.65	2.306547908	0.8195979758	2.347527807	0.8946013641	2.349402892
4	0.05	1.7	2.349402892	0.8930075421	2.394053269	0.9677033899	2.395920665
5	0.05	1.75	2.395920665	0.9660694182	2.444224136	1.040198278	2.446077357
6	0.05	1.8	2.446077357	1.038530378	2.498003876	1.111846414	2.499836777
7	0.05	1.85	2.499836777	1.110150981	2.555344326	1.18242289	2.557151124
8	0.05	1.9	2.557151124	1.180706432	2.616186446	1.251718216	2.61796174
9	0.05	1.95	2.61796174	1.249987303	2.680461105	1.319538895	2.682199895
10	0.05	2	2.682199895	1.317800105	2.7480899	1.385707852	2.749787594
11	0.05	2.05	2.749787594	1.383967716	2.81898598	1.450064721	2.820638405
12	0.05	2.1	2.820638405	1.448329675	2.893054889	1.512465995	2.894658297
13	0.05	2.15	2.894658297	1.510742331	2.970195413	1.572785045	2.971746481
14	0.05	2.2	2.971746481	1.571078871	3.050300425	1.630912022	3.051796253
15	0.05	2.25	3.051796253	1.629229215	3.133257714	1.686753629	3.134695825
16	0.05	2.3	3.134695825	1.685099802	3.218950815	1.740232793	3.220329139
17	0.05	2.35	3.220329139	1.738613261	3.307259802	1.791288237	3.308576677
18	0.05	2.4	3.308576677	1.789707988	3.398062076	1.839873957	3.399316225
19	0.05	2.45	3.399316225	1.838337624	3.491233107	1.885958617	3.492423631
20	0.05	2.5	y(2) = 3.492423631

Runge-Kutta
i	h	x_i	y_i	k1 = f(x_i,y_i)	k2 = f(x_i+.5h,y_i+.5hk1)	k3 = f(x_i+.5h, y_i+.5hk2)	k4 = f(x+h,y+hk3)	Runge-Kutta y_(i+1) = y_i + h*(k1+2k2+2k3+k4)/6
0	0.05	1.5	2.2	0.6	0.6366875	0.6359881445	0.6728554594	2.23181839
1	0.05	1.55	2.23181839	0.6728407481	0.709821466	0.7090934081	0.746181552	2.267292157
2	0.05	1.6	2.267292157	0.7461662747	0.7832936203	0.7825394711	0.8197042176	2.306438296
3	0.05	1.65	2.306438296	0.8196884061	0.8568207014	0.856043244	0.8931456109	2.349259645
4	0.05	1.7	2.349259645	0.8931293019	0.9301304558	0.9293326184	0.9662395087	2.395745436
5	0.05	1.75	2.395745436	0.9662227434	1.002962858	1.002147687	1.038732462	2.445871905
6	0.05	1.8	2.445871905	1.038715285	1.075071194	1.074241825	1.110384803	2.499602956
7	0.05	1.85	2.499602956	1.110367265	1.146222996	1.145382627	1.180971517	2.556890873
8	0.05	1.9	2.556890873	1.18095367	1.216200837	1.215352702	1.250282954	2.617677071
9	0.05	1.95	2.617677071	1.250264856	1.284802979	1.283950319	1.318125413	2.681892878
10	0.05	2	2.681892878	1.318107122	1.351843875	1.350989913	1.384321567	2.749460347
11	0.05	2.05	2.749460347	1.384303145	1.417154527	1.416302445	1.448710757	2.820293079
12	0.05	2.1	2.820293079	1.448692267	1.480582715	1.479735625	1.51114915	2.894297063
13	0.05	2.15	2.894297063	1.511130657	1.541993079	1.541154007	1.57150976	2.971371518
14	0.05	2.2	2.971371518	1.57149133	1.601267084	1.600438946	1.629682352	3.051409732
15	0.05	2.25	3.051409732	1.629664051	1.658302858	1.657488442	1.685573222	3.134299898
16	0.05	2.3	3.134299898	1.685555117	1.713014923	1.712216872	1.739104879	3.219925928
17	0.05	2.35	3.219925928	1.739087035	1.765333814	1.764554613	1.79021561	3.308168257
18	0.05	2.4	3.308168257	1.790198091	1.815205609	1.814447568	1.838858971	3.398904619
19	0.05	2.45	3.398904619	1.838841842	1.862591365	1.861856614	1.885003188	3.492010794
20	0.05	2.5	y(2.5) = 3.492010794

OpenLab #2: Numerical methods PROJECT – Part 1

March 12, 2019 / Jonas Reitz / 2 Comments

Numerical methods provide a way to compute (approximate) values of solutions to differential equations, even when we cannot solve the equations exactly. The drawback is the large number of numerical calculations required to obtain a desired value and level of precision. In this project, you will use technology to implement the various numerical methods and use your technological solution to solve differential equations problems.

Assignment (Due Tuesday, April 4th). Create a numerical methods calculator. You can choose your technology tool for this job – use any one of the following:

a spreadsheet (Excel, Google Sheets, or other spreadsheet)
- if you choose to create a spreadsheet, you should have columns for $x, y, f(x,y)$ , and so on, and each stage should appear in its own row
a programming language (Java, Perl, or other programming language)
- if you choose to write code, your program should output the values of $x, y, f(x,y)$ and so on at each stage
mathematical software (MatLab, Maple, Mathematica, or other mathematical software)
- if you choose to use mathematical software, your program should output the values of $x, y, f(x,y)$ and so on at each stage

How to submit. Part 2 of this project will talk about how to submit your project – you will be asked to upload your solution (spreadsheet, or code, or mathematical software document) and to write about what you did. For now, focus on getting your solution working.

Requirements:

Your solution should allow you to solve problems of this type:

Example. Given the differential equation 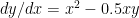and initial condition , approximate the value of 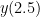using step size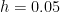

Your solution must be able to carry out Euler’s Method, Improved Euler’s Method, and Runge-Kutta (you may implement these as three separate spreadsheets or programs if you wish).
Your solution should display all the points 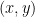$(x,y)$ found along the way, not just the final point.
Your solution should also display other values found while carrying out each method:
1. Euler’s Method: display the slope 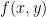$f(x,y)$ at each stage
2. Improved Euler’s: display the values of 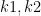$k1, k2$ at each stage
3. Runge-Kutta: display the values of 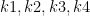$k1, k2, k3, k4$ at each stage
4. You can display other values as well, if you wish (for example, the intermediate y-value in the Improved Euler method that we refer to as $z$ ).
Your solution may NOT use any built-in version of these methods (for example, most mathematical software contains a built-in command for Euler’s Method – you can use this to check your work, but you need to create your own solution).
You should be able to relatively easily change the initial condition, step size, and target value.
You should be able to relatively easily change the differential equation (it is ok if the equation is hard-coded into your program).

Test your project. Solution data for the above example using Euler, Improved Euler, and Runge-Kutta will be posted this weekend so you can test your project. You can also use examples from class to test your work, since you know what the solutions are.

OpenLab #1: Advice from the Past

February 5, 2019 / Jonas Reitz / 50 Comments

In Fall 2014 I taught this course and at the end of the semester, I gave my students the following assignment:

Imagine that you are invited to speak on the first day of MAT 2680, to give advice to entering students. Write at least three sentences … describing what you would tell them.

To see the assignment and the students’ responses, follow this link.

Your assignment, due at the beginning of class next Thursday, February 14th, is to:

Read through ALL the responses (there are 63 of them, but many of these are short replies to other comments).
Write a reply to this post (1 paragraph) responding to all of the following:
1. What advice seemed most relevant to you personally? Why? (you can copy/paste a short statement, or put it in your own words)
2. Based on this advice, what changes can you make right now to help you succeed in this course?

Extra Credit. For extra credit, write a response to one of your classmates’ comments. Do you have any advice? Be kind.