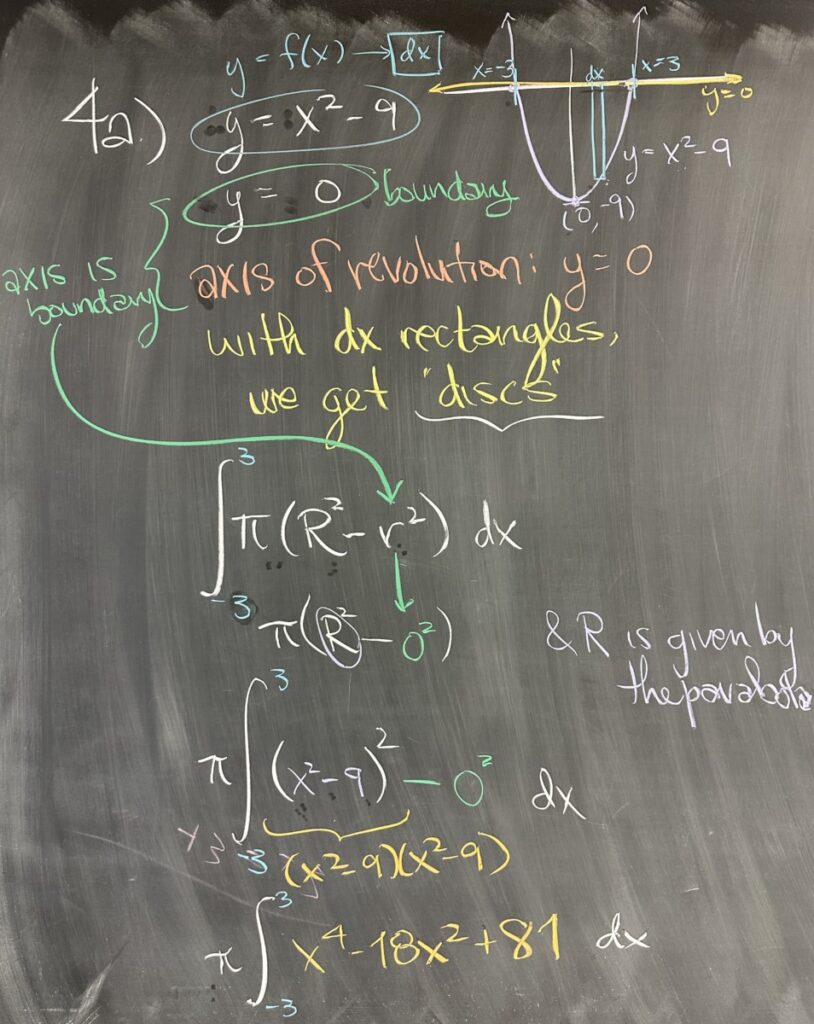
Starting with problem four on the Final Exam Review sheet, we looked at part a. The region described is bounded by a parabola \(y = x^2-9\) and the \(x\)-axis, \(y=0\). Because the region defines \(y\) as a function of \(x\), this is an indication that we will use \(dx\) rectangles. Because \(dx\) rectangles are vertically oriented, and our axis of revolution is the (horizontally oriented) \(x\)-axis, the two are perpendicular — and we conclude that this situation requires the “disc” or “washer” method.
Since our axis of revolution is also a boundary for our region, we know that the inner radius for the “washer” method will be zero.
We also look at where our boundaries intersect in order to determine the \(x\)-interval over which we will integrate using the “disc/washer” method. \(y=0\) intersects \(y=x^2-9\) whenever \(0=x^2-9\), which has solutions \(x=-3\) and \(x=3\).
Our radius for each disc is given by the \(y\)-value of the parabola, \(y=x^2-9\), so the integral for the volume will be as follows: \[\int_{-3}^3 \pi\left(x^2-9\right)^2 \, dx = \pi\int_{-3}^3 x^4 – 18x^2 + 81\, dx\]

The integral only requires the power rule for antiderivatives, after which all that remains is to evaluate at \(x=3\) and \(x=-3\) and subtract the resulting values.

The next volume of revolution problem uses a region that is bounded by three lines. On the left side, we have the vertical line \(x=-1\), and on the right side we have two other lines, both given with \(x\) as the independent variable. This is again an indication that we should be using “dx” (vertical) rectangles.
We find that our two lines on the right side of the region intersect at the point \((1,15)\), suggesting that the \(x\)-bounds will be \([-1,1]\).
Again, our axis of revolution is the \(x\)-axis (horizontal). With the rectangles and axis oriented perpendicularly to each other, we again find ourselves using the disc/washer method. This time, however, the axis of revolution is NOT a boundary for our region, so we must determine both the “inner” radius, \(r\), as well as the “outer” radius, \(R\).
Looking at the graphed region, we can see that the line \(y=3x+12\) is closer to the axis of revolution, and the line \(y=16-x\) is farther from the axis. The closer boundary forms the “inner” radius while the farther boundary forms the “outer” radius.

Setting up the washer method with our “inner” and “outer” radii, we get the following integral: \[\int_{-1}^1 \pi\left(16-x\right)^2-\pi\left(3x+12\right)^2\,dx = \pi\int_{-1}^1 \left(256-32x+x^2\right)-\left(9x^2+72x+144\right)\,dx\]
To finish computing the volume we can combine like terms, then find the antiderivative using the power rule, and wrap it up by evaluating at the bounds and subtracting the results.
For the third volume problem we are given two parabolas (both use \(x\) as the independent variable, so again “dx” rectangles). We are also told that \(x\geq0\), so we only need to find intersections where \(x\) is positive. The two parabolas intersect at \(x=-2\) (which we ignore) and \(x=2\), giving us an interval \([0,2]\).
However, this time, our axis of revolution is the \(y\)-axis — which is parallel to our vertical “dx” rectangles. This means we’ll be using the shell method.

When using the shell method, the radius is given by the distance from our independent variable to the axis of revolution. In our case, the axis is \(x=0\), so the radius is \(R=x-0\).
The height of the cylinder (shell) is the height of our rectangle. Our rectangles are vertical, so this will be measured as the distance between the upper and lower boundaries of our region. The \(y=10-x^2\) parabola is our upper bound for the region, and the \(y=x^2+2\) parabola forms the lower bound. This makes the height of our “shell”: \(H = (10-x^2)-(x^2+2) = 8-2x^2\).
Then, when we use the shell method, we get the following integral:\[\int_0^2 2\pi x(8-2x^2)\,dx = 2\pi\int_0^2 8x-2x^3\,dx\]
Again, this can be computed using the power rule and finishing with the Fundamental Theorem of Calculus.

We also reviewed trig substitution, and in problem 5a, we see an integral containing \(\sqrt{36-x^2}\). This follows the pattern of \(\cos^2(\theta) = 1-\sin^2(\theta)\), and in order to match the \(36\), we must substitute \(x=6\sin(\theta)\). The differential for this substitution is \(dx = 6\cos(\theta)\,d\theta\), resulting in the substituted integral \[\int \frac{1}{36\sin^2(\theta)\sqrt{36-36\sin^2(\theta)}}\,6\cos(\theta)\,d\theta\]
We can reduce \(36-36\sin^2(\theta) = 36\cos^2(\theta)\), whose square root is \(6\cos(\theta)\). We can then reduce that same factor from the differential with the square root in the denominator to end up with the simplified integral: \[\int \frac{1}{36\sin^2(\theta)}\,d\theta\]

This is the integral of cosecant squared, as cosecant is the reciprocal of sine. Cosecant squared has antiderivative \(-\cot(\theta)\), where cotangent is the reciprocal of tangent (adjacent over opposite).
Using the right triangle formed by our original substitution \(x=6\sin(\theta)\) or \(\frac{x}{6} = \sin(\theta)\), we then use the Pythagorean Theorem to determine the opposite side: \(\sqrt{36-x^2}\), ultimately finding that the cotangent ratio is \(\frac{\sqrt{36-x^2}}{x}\).

We then talked a bit about improper integrals and their relationship to p-Series. The function \(y=\frac{1}{x}\) is symmetric about the line \(y=x\). This means that the asymptotic behavior of the function is the same for both the horizontal and vertical asymptotes. Neither of these regions is finite, so their improper integrals both diverge.
However, when p is different from \(1\), there is no symmetry and we end up with one side giving a finite region while the other is infinite. When \(p>1\), the horizontal asymptote region is finite while the vertical is infinite. When \(p<1\), the behavior reverses with the horizontal region being infinite and the vertical being finite.

In our final example, we looked at an improper integral with a vertical asymptote at \(x=3\). It is essential in these problems that we re-write the integral as a limit! We cannot use the Fundamental Theorem of Calculus unless we first re-write the integral as a limit.
In this case, we end up with a p-value of \(\frac{4}{3}\), which is greater than one. Because our asymptote is vertical and \(p\) is greater than one, we expect that this limit will be infinite.
If we compute the antiderivative, we have \[\lim_{a\to 3^+} \left[\left(x-3\right)^{-\frac{1}{3}} \right]_a^5\]
Because of the negative exponent, when \(a\) approaches \(3^+\), this will have the result of approaching zero in the denominator, giving an infinite (divergent) conclusion.



Recent Comments