Note: Strictly speaking, partial fraction decomposition is a technique that is not specific to the task of integration.
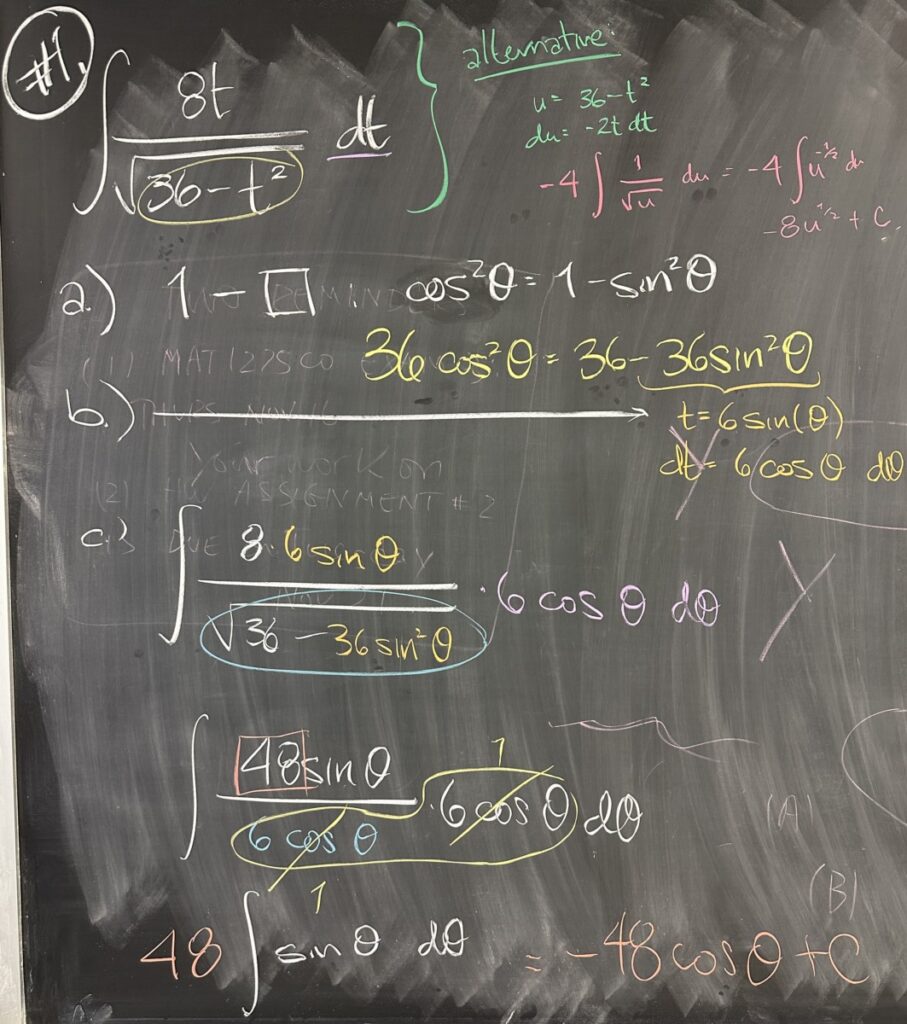
Parker | D538 | Spring 2024
Note: Strictly speaking, partial fraction decomposition is a technique that is not specific to the task of integration.
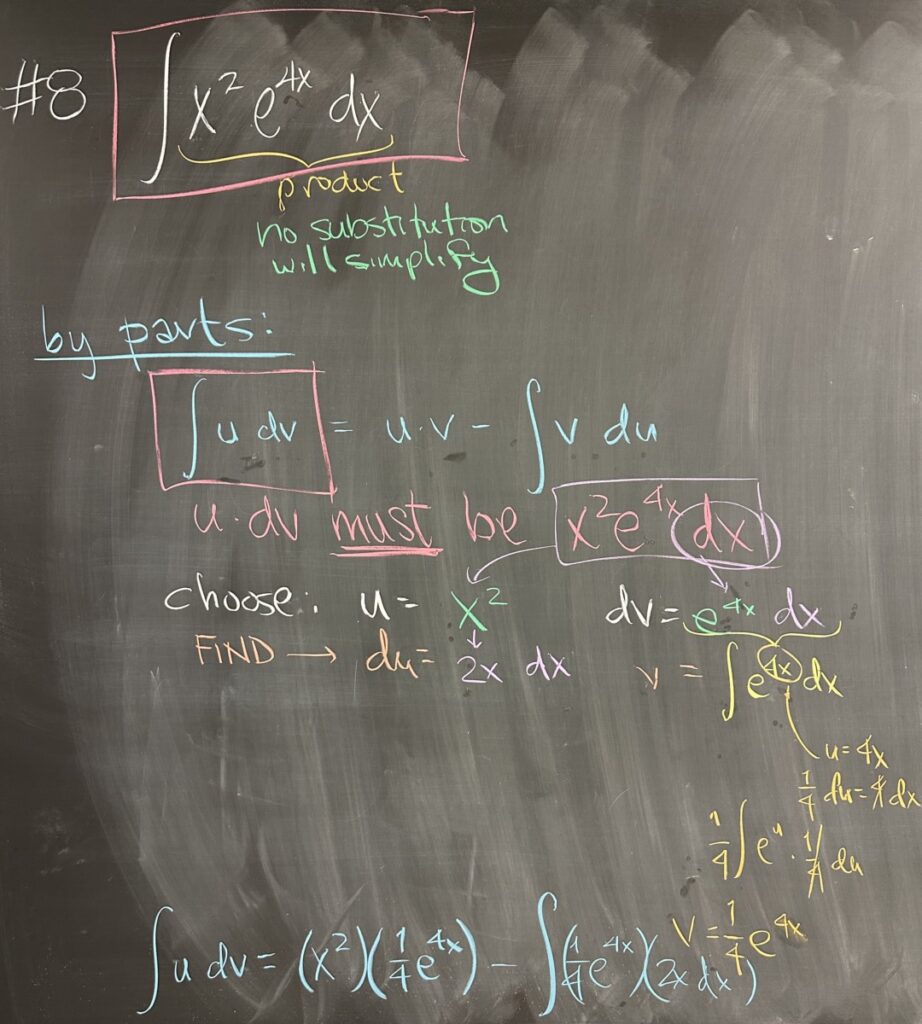
Instead of having a quiz today, we discussed a few problems from Thursday’s exam. The first problem we looked at was the indefinite integral: \(\int x^2 e^{4x}\,dx\). It is crucial to develop an intuition for the choice between u-substitution and integration by parts. This integral does not have a simplifying u-substitution, which can be difficult to determine if you haven’t been practicing your antiderivative skills on the homework.
Continue reading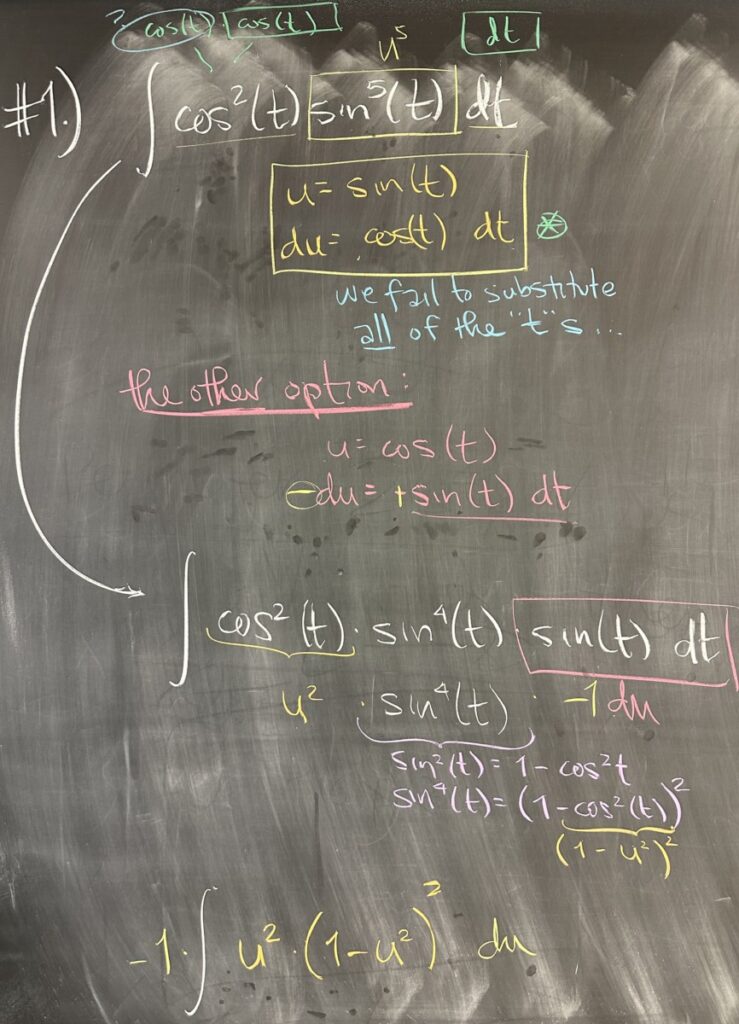
Today’s quiz focused on integrating products of powers of trig functions. In these situations, we see powers of sine and cosine multiplied, or similarly secant and tangent. In our first problem, we have \(\int \cos^2(t)\sin^5(t)\,dt\).
Continue reading© 2024 MAT1575 Calculus2 S24
Theme by Anders Noren — Up ↑
Recent Comments